辽宁省鞍山市2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下面各数比 $- \sqrt{2}$ 大的数是（）

A、 $- π$ B、 $- \sqrt{3}$ C、 $- \frac{1}{2}$ D、-1.5

查看试题解析
2. 下面各组 $x$ 、 $y$ 的值满足二元一次方程 $3 x + y = 5$ 的是（）

A、 $x = - 2$ ， $y = 1$ B、 $x = 0$ ， $y = 5$ C、 $x = 2$ ， $y = 1$ D、 $x = 5$ ， $y = 0$

查看试题解析
3. 若 $a > b$ ，则下列不等式成立的是（）

A、 $- a > - b$ B、 $a + b > 0$ C、 $\frac{1}{2} a > b$ D、 $2 a - 5 > 2 b - 5$

查看试题解析
4. 经调查，某班学生上学所用的交通工具中公交车占 $20 %$ ，校车占 $30 %$ ，私家车占 $40 %$ ，其它占 $10 %$ ，为了描述这些数据最好采用（）

A、扇形图 B、条形图 C、折线图 D、直方图

查看试题解析
5. 如图，平行线 $A B$ ， $C D$ 被直线 $A E$ 所截， $∠ 1 = 110 °$ ，则下列结论正确的是（）

A、 $∠ 2 = 110 °$ B、 $∠ 3 = 70 °$ C、 $∠ 4 = 70 °$ D、 $∠ 5 = 70 °$

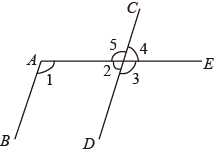查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt[3]{- 8} = - 2$ C、 $\sqrt[3]{9} = 3$ D、 $\sqrt{1.44} = 0.12$

查看试题解析
7. 下列各命题中，是真命题的是（　　）

A、同位角相等 B、内错角相等 C、邻补角相等 D、对顶角相等

查看试题解析
8. 《孙子算经》中有一道题，原文是：“今有木，不知长短。引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺，将绳子对折再量长木，长木还剩余1尺，问木长多少尺？如果设木长 $x$ 尺，绳子长 $y$ 尺，则下列方程组正确的是（）

A、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ B、 ${\begin{array}{l} y - x = 4.5 \\ \frac{1}{2} y - x = 1 \end{array}$ C、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ D、 ${\begin{array}{l} y - x = 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$

查看试题解析
9. 在平面直角坐标系中，一个智能机器人接到如下指令：从原点 $O$ 出发，按向右，向上，向右，向下的方向依次不断移动，每次移动 $1 m$ .其行走路线如图所示，第1次移动到 $A_{1}$ ，第2次移动到 $A_{2}$ ，…，第 $n$ 次移动到 $A_{n}$ ．则 $△ O A_{2} A_{2021}$ 的面积是（）

A、 $504 m^{2}$ B、 $505 m^{2}$ C、 $\frac{1011}{2} m^{2}$ D、 $506 m^{2}$

查看试题解析

二、填空题

10. 已知 $x$ 的一半与5的差小于3，用不等式表示为．

查看试题解析
11. 已知 $\sqrt{{(a - 2)}^{2}} = 1$ ，则 $a$ 的值是．

查看试题解析
12. 如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB=90°）在直尺的一边上，若∠1=25°，则∠2的度数等于.

查看试题解析
13. 进行数据的调查收集，一般可分为以下六个步骤，但它们的顺序弄乱了，正确的顺序是． (用字母按顺序写出即可)
A．明确调查问题；B．记录结果；C．得出结论；D．确定调查对象；E．展开调查；F．选择调查方法.

查看试题解析
14. 在平面直角坐标系中，已知点 $P$ 的坐标为 $(2 m + 1 ， 5 - 4 m)$ ，若点 $P$ 在第四象限，那么 $m$ 的取值范围是．

查看试题解析
15. 小丽想用一块面积为 $400 {cm}^{2}$ 的正方形纸片，沿着边的方向裁出一块面积为 $222 {cm}^{2}$ 的长方形纸片，使它的长宽之比为 $3 ： 2$ ，则这个长方形的边长分别是．

查看试题解析

三、解答题

16. 解下列方程组：

(1)、 ${\begin{array}{l} \frac{2 x}{3} + \frac{3 y}{4} = 6 \\ \frac{x}{6} - \frac{y}{2} = - \frac{1}{3} \end{array}$ ；

(2)、 ${\begin{array}{l} y = 2 x - 7 \\ 5 x + 3 y + 2 z = 2 \\ 3 x - 4 z = 4 \end{array}$ ．

查看试题解析
17. 解不等式 $\frac{1}{3} (1 - 2 x) \geq \frac{3 (2 x - 1)}{2}$ ；并写出它所有的非负整数解．

查看试题解析
18. 已知，在四边形 $A B C D$ 中， $A B ⊥ B C$ ， $D C ⊥ B C$ ， $∠ D = 40 °$ ，若 $B E ⊥ A C$ ， $A D / / B E$ ，试求出 $∠ B A C$ 的度数．

查看试题解析
19. 如图，在平面直角坐标系中，

(1)、写出点 $A$ ， $B$ ， $C$ 三个点的坐标；

(2)、画出三角形 $A B C$ 向右平移6个单位后的图形三角形 $A_{1} B_{1} C_{1}$ ；

(3)、将线段 $B C$ 向下平移2个单位得到 $B_{2} C_{2}$ ，求四边形 $B B_{2} C_{2} C$ 的面积．

查看试题解析
20. 每年4月23日为世界读书日，学校计划购进一批科普读物，想了解本校九年级学生对哪门课程感兴趣，随机抽取了部分九年级学生进行调查（每名学生只能选择一门课程）.将获得的数据整理绘制成如图两幅不完整的统计图.

根据统计图提供的信息，解答下列问题：

(1)、 $m$ 的值是；

(2)、请补全条形统计图；

(3)、若该校九年级共有500名学生，请你估计该校九年级学生中大约有多少名学生对数学感兴趣？

查看试题解析
21. 为了加强对校内外安全监控，创建平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备．经调查，购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元．

(1)、求甲乙两种型号监控设备每台的价格；

(2)、若购买该批设备的资金不超过11000元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？

查看试题解析
22. 在平面直角坐标系中， $O$ 为坐标原点，点A的坐标为 $(a ， 0)$ ，点 $B$ 坐标为 $(0 ， b)$ ，且 $a$ ， $b$ 满足 ${\begin{array}{l} 3 a + 2 b = 0 \\ a + b = 1 \end{array}$ ．

(1)、求A ， $B$ 两点的坐标；

(2)、若点 $C$ 的坐标为 $(c ， c)$ ，且满足 $∠ ABO + ∠ BAC = 180 °$ ，求出 $C$ 点坐标；

(3)、在 $x$ 轴上找一点 $D$ ，使三角形 $A C D$ 的面积是三角形 $A B C$ 面积的2倍，请直接写出点 $D$ 的坐标．

查看试题解析