上海市静安区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、填空题

1. 0.01的平方根是.

查看试题解析
2. 已知 $a^{3} = 216$ ，那么 $a =$ ．

查看试题解析
3. 已知实数 $a \leq 0 \leq b$ ，化简： $\sqrt{{(a - b)}^{2}} =$ ．

查看试题解析
4. 计算： $4^{- \frac{3}{2}} =$ ．

查看试题解析
5. 月球沿着一定的轨道围绕地球运动，它的半长轴约为385000千米，这个数据用科学记数法精确到万位表示，应记为千米．

查看试题解析
6. 对于近似数0.0680，它有个有效数字．

查看试题解析
7. 在平面直角坐标系中，经过点 $A (- 3 ， 4)$ 且垂直于 $y$ 轴的直线可以表示为直线．

查看试题解析
8. 在平面直角坐标系中，如果点 $Q (a + 1 ， 2 - a)$ 在 $x$ 轴上，那么 $a =$ ．

查看试题解析
9. 如图，直线AB和直线CD相交于点O ， ∠AOC＝50°，OE平分∠BOD ，那么∠BOE＝度．

查看试题解析
10. 如图，过直线外一点D画已知直线AB的平行线．首先画直线AB ，将三角尺的一边紧靠直线AB ，将直尺紧靠三角尺的另一边；然后将三角尺沿直尺下移；最后当三角尺原紧靠直线AB的那一边经过点D时，画直线CD ．这样就得到CD∥AB ．这种画法的依据是．

查看试题解析
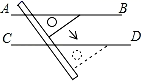11. 如图，△ABC的三个顶点分别在直线a、b上，且a∥b，若∠1＝120°，∠2＝80°，则∠3的度数是．

查看试题解析
12. 已知等腰三角形的两条边长分别是3cm、7cm，那么这个等腰三角形的周长是 cm．

查看试题解析
13. 如图，五边形ABCDE中，AB∥DE ， BC⊥CD ， ∠1、∠2分别是与∠ABC、∠CDE相邻的外角，则∠1+∠2等于度．

查看试题解析
14. 已知 $Δ A B C$ 中， $A B = A C$ ， $∠ B = 50 °$ ，如果 $D$ 是边 $B C$ 的中点，那么 $∠ C A D =$ 度．

查看试题解析
15. 在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称该点是整点，如果整点 $P (2 m - 1 ， m + 2)$ 在第二象限，那么 $m$ 的值为．

查看试题解析

二、单选题

16. 如图，数轴上点 $P$ 表示的数可能是（）

A、 $- \sqrt{5}$ B、 $\sqrt{5}$ C、 $- 3.7$ D、 $- \sqrt{2}$

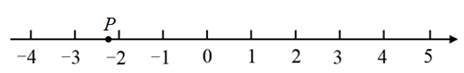查看试题解析
17. 下列说法正确的是（）

A、周长相等的锐角三角形都全等 B、周长相等的直角三角形都全等 C、周长相等的钝角三角形都全等 D、周长相等的等边三角形都全等

查看试题解析
18. 若∠A，∠B互为补角，且∠A＜∠B，则∠A的余角是（　　）

A、 $\frac{1}{2}$ （∠A+∠B） B、 $\frac{1}{2}$ ∠B C、 $\frac{1}{2}$ （∠B﹣∠A） D、 $\frac{1}{2}$ ∠A

查看试题解析
19. 在平面直角坐标系中，点 $B$ 在第四象限，它到 $x$ 轴和 $y$ 轴的距离分别是2、5，则点 $B$ 的坐标为（）

A、 $(5 ， - 2)$ B、 $(2 ， - 5)$ C、 $(- 5 ， 2)$ D、 $(- 2 ， - 5)$

查看试题解析
20. 早晨8：00以后，时钟的分针和时针第一次垂直的准确时间是（）

A、8点 $23 \frac{1}{13}$ 分 B、8点25分 C、8点 $27 \frac{3}{11}$ 分 D、9点整

查看试题解析

三、解答题

21. 计算： ${(2 - \sqrt{3})}^{0} + {(\frac{1}{\sqrt{3}})}^{- 1} - \sqrt{{(2 - \sqrt{3})}^{2}}$ ．

查看试题解析
22. 计算： $(- \sqrt{2} + 3 \sqrt{2}) \times \sqrt{2} - \sqrt{20} \div \sqrt{5}$ ．

查看试题解析
23. 用幂的性质计算： ${(5 - 17^{\frac{1}{2}})}^{\frac{1}{3}} \cdot {(5 + 17^{\frac{1}{2}})}^{\frac{1}{3}}$ ．

查看试题解析
24. 计算： $\sqrt{8} \times \sqrt[3]{4} \div \sqrt[6]{2}$ ．

查看试题解析
25. 如图，已知在 $Δ A B C$ 中， $F G / / E B$ ， $∠ 2 = ∠ 3$ ，说明 $∠ E D B + ∠ D B C = 180 °$ 的理由．
解：∵ $F G / / E B$ （    ），

∴   ▲   $=$    ▲   （     ）．

∵ $∠ 2 = ∠ 3$ （已知），

∴   ▲   $=$    ▲   （    ）．

∴ $D E / / B C$ （     ），

∴ $∠ E D B + ∠ D B C = 180 °$ （     ）．

查看试题解析
26. 平面直角坐标系中，点 $A (x ， y)$ ，如果 $x$ 的两个平方根分别是 $2 y - 3$ 与 $1 - y$ ．

(1)、求点 $A (x ， y)$ 的坐标；

(2)、点 $A (x ， y)$ 沿 $x$ 轴的方向向右平移多少个单位后落在第一和第三象限的平分线上？

查看试题解析
27. 如图已知 $Δ A B C$ 的三个顶点的坐标分别是 $A (- 2 ， 3)$ ， $B (0 ， 1)$ ， $C (2 ， 2)$ ．

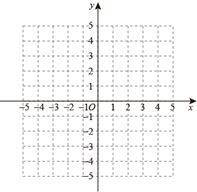(1)、在所给的平面直角坐标系中画出 $Δ A B C$ ；

(2)、求出 $Δ A B C$ 的面积；如果点 $P$ 的坐标为 $(4 ， 0)$ ，请直接判断 $Δ P A C$ 和 $Δ A B C$ 的面积是否相等．

查看试题解析
28. 如图，在△ABC中，BD=DC ， ∠1=∠2，求证：AD是∠BAC的平分线．

查看试题解析
29. 如图，已知四边形ABCD中，AB∥CD ， AD∥BC ． E为BD上一点，且BE＝AD ， ∠DEF＝∠ADC ， EF交BC的延长线于点F ．

(1)、AD和BC相等吗？为什么？

(2)、BF和BD相等吗？为什么？

查看试题解析
30. 如图，在直角坐标平面内有点 $A (0 ， 2)$ 、 $B (- 2 ， 0)$ 、 $C (2 ， 0)$ ．

(1)、 $Δ A B C$ 的形状是否是等腰直角三角形？为什么？

(2)、课文阅读材料告诉我们，古希腊的希帕斯经过探索，发现了如此情况下 $A B$ 的长是一个无理数，请你（不用勾股定理等后面所学习的方法）求出 $A B$ 的长，以此向古代先贤致敬；

(3)、点 $P$ 在 $y$ 轴上，如果 $Δ P A B$ 是等腰三角形，请直接写出点 $P$ 的坐标．

查看试题解析