山东省济南市章丘区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. ﹣ 的绝对值是( )A、﹣ B、 C、 D、±2. 如图所示,这是由4个大小相同的小正方体摆成的几何体,从左面看到的几何体的形状图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 2020年,面对新冠肺炎疫情和不利天气影响,中国粮食产量创历史最高水平,达到13390亿斤,连续六年稳定在13000亿斤以上,其中13000亿用科学记数法表示为( )A、13×1011 B、1.3×1012 C、1.3×1011 D、0.13×10134. 下列调查中,调查方式选择合理的是( )A、要了解全济南初中学生的业余爱好,采用普查的方式 B、调查你所在班级同学的身高,采用抽样调查的方式 C、调查市场上华为手机的使用寿命,采用普查的方式 D、调查章丘百脉泉的水质情况,采用抽样调查的方式5. 若2x3nym+4与﹣3x9y2n可以合并为一项,那么m+n的值是( )A、2 B、3 C、5 D、86. 下列各式计算正确的是( )A、3x+3y=6xy B、6x+5=6(x+5) C、﹣y2﹣y2=0 D、﹣a+b=﹣(a﹣b)7. 已知 是关于x的方程 的解,则a的值为A、 B、 C、 D、18. 2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线, 不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体 中,与汉字“抗”相对的面上的汉字是( )
3. 2020年,面对新冠肺炎疫情和不利天气影响,中国粮食产量创历史最高水平,达到13390亿斤,连续六年稳定在13000亿斤以上,其中13000亿用科学记数法表示为( )A、13×1011 B、1.3×1012 C、1.3×1011 D、0.13×10134. 下列调查中,调查方式选择合理的是( )A、要了解全济南初中学生的业余爱好,采用普查的方式 B、调查你所在班级同学的身高,采用抽样调查的方式 C、调查市场上华为手机的使用寿命,采用普查的方式 D、调查章丘百脉泉的水质情况,采用抽样调查的方式5. 若2x3nym+4与﹣3x9y2n可以合并为一项,那么m+n的值是( )A、2 B、3 C、5 D、86. 下列各式计算正确的是( )A、3x+3y=6xy B、6x+5=6(x+5) C、﹣y2﹣y2=0 D、﹣a+b=﹣(a﹣b)7. 已知 是关于x的方程 的解,则a的值为A、 B、 C、 D、18. 2020年是不寻常的一年,病毒无情人有情,很多最美逆行者奔赴疫情的前线, 不顾自己的安危令我们感动.宣传委员小明在一个正方体的每个面上分别写上一个汉字,组成“共同抗击疫情”.如图是该正方体的一种展开图,那么在原正方体 中,与汉字“抗”相对的面上的汉字是( )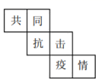 A、 共 B、同 C、疫 D、情9. 如图,OC是∠AOB的平分线,∠BOD= ∠COD,∠BOD=20°,则∠AOB的度数为( )
A、 共 B、同 C、疫 D、情9. 如图,OC是∠AOB的平分线,∠BOD= ∠COD,∠BOD=20°,则∠AOB的度数为( )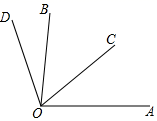 A、100° B、80° C、60° D、40°10. 超市正在热销某种商品,其标价为每件125元,若这种商品打8折销售,则每件可获利15元,设该商品每件的进价为x元,根据题意可列出的一元一次方程为( )A、125×0.8﹣x=15 B、125﹣x×0.8=15 C、(125﹣x)×0.8=15 D、125﹣x=15×0.811. 如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=m,NB=n,则线段MN的长是( )
A、100° B、80° C、60° D、40°10. 超市正在热销某种商品,其标价为每件125元,若这种商品打8折销售,则每件可获利15元,设该商品每件的进价为x元,根据题意可列出的一元一次方程为( )A、125×0.8﹣x=15 B、125﹣x×0.8=15 C、(125﹣x)×0.8=15 D、125﹣x=15×0.811. 如图,点C是线段AB上一点,AC<CB,M、N分别是AB和CB的中点,AC=m,NB=n,则线段MN的长是( )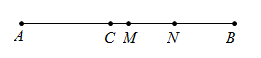 A、m﹣n B、m﹣ n C、n+ m D、 m12. a是不为1的有理数,我们把 称为a的差倒数,如2的差倒数为 ,-1的差倒数为 ,已知 , 是 差倒数, 是 差倒数, 是 差倒数,以此类推……, 的值是( )A、5 B、 C、 D、
A、m﹣n B、m﹣ n C、n+ m D、 m12. a是不为1的有理数,我们把 称为a的差倒数,如2的差倒数为 ,-1的差倒数为 ,已知 , 是 差倒数, 是 差倒数, 是 差倒数,以此类推……, 的值是( )A、5 B、 C、 D、二、填空题
-
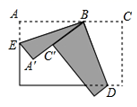
13. 2021年1月7日受强冷空气影响,山东多地气温大幅下降.章丘区最低气温为﹣23.8℃,最高气温为﹣9℃,这天的日温差是 ℃.14. 如果代数式4y2﹣2y+5的值为1,那么代数式2y2﹣y+1的值为 .15. 过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的边数是 .16. 若代数式2﹣8x与9x﹣3的值互为相反数,则x= .17. 将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕。则∠EBD=度.
 18. 如图是用棋子摆成的“ ”字图案.从图案中可以看出,第1个“ ”字图案需要4枚棋子,第2个“ ”字图案需要7枚棋子,第3个“ ”字图案需要10枚棋子.照此规律,摆成第 个“ ”字图案需要2020枚棋子,则 的值为 .
18. 如图是用棋子摆成的“ ”字图案.从图案中可以看出,第1个“ ”字图案需要4枚棋子,第2个“ ”字图案需要7枚棋子,第3个“ ”字图案需要10枚棋子.照此规律,摆成第 个“ ”字图案需要2020枚棋子,则 的值为 .
三、解答题
-
19. 计算(1)、4+(﹣2)2×2﹣(﹣36)÷4;(2)、16÷(﹣2)3﹣( )×(﹣4).20. 先化简,再求值:5(3a2b-ab2)-(ab2+3a2b),其中a=- ,b=2.21.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
 22. 解方程(1)、5x+2=3(x+2)(2)、 .23. 如图,已知点D是线段AB上的一点,延长线段AB至C,使得AB=BC,且DC=5AD,若BD=4cm,求线段AC的长.
22. 解方程(1)、5x+2=3(x+2)(2)、 .23. 如图,已知点D是线段AB上的一点,延长线段AB至C,使得AB=BC,且DC=5AD,若BD=4cm,求线段AC的长. 24. 居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:
24. 居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;
B.赞同但要有时间限制;
C.无所谓;
D.不赞同.
并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)、求本次被抽查的居民有多少人?(2)、将图1和图2补充完整;(3)、求图2中“C”层次所在扇形的圆心角的度数;(4)、估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.25. 在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与爸爸的对话(如图),请根据图中的信息,解答下列问题: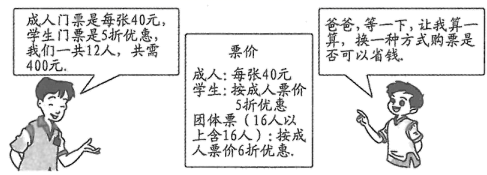 (1)、他们共去了几个成人,几个学生?(2)、请你帮他们算算,用哪种方式购票更省钱?26. 乐乐对几何中角平分线部分的学习兴趣浓厚,请你和乐乐一起探究下面问题吧.已知∠AOB=100°,射线OE、OF分别是∠AOC和∠COB的平分线.
(1)、他们共去了几个成人,几个学生?(2)、请你帮他们算算,用哪种方式购票更省钱?26. 乐乐对几何中角平分线部分的学习兴趣浓厚,请你和乐乐一起探究下面问题吧.已知∠AOB=100°,射线OE、OF分别是∠AOC和∠COB的平分线. (1)、如图1,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF的度数;(2)、如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数;(3)、若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC,均指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,请直接写出∠EOF的度数.(不写探究过程)27. 已知a为最大的负整数,b是﹣5的相反数,c=﹣|﹣2|,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)、如图1,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF的度数;(2)、如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数;(3)、若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC,均指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,请直接写出∠EOF的度数.(不写探究过程)27. 已知a为最大的负整数,b是﹣5的相反数,c=﹣|﹣2|,且a,b,c分别是点A,B,C在数轴上对应的数. (1)、求a,b,c的值,并在数轴上标出点A,B,C.(2)、若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?(3)、若动点P从点B出发,以每秒3个单位的速度向右运动,点C以每秒1个单位的速度向左运动,点A以每秒2个单位的速度向右运动,三点同时出发,设运动时间为t秒,试判断4AP﹣CP的值是否会随着t的变化而变化?请说明理由.
(1)、求a,b,c的值,并在数轴上标出点A,B,C.(2)、若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?(3)、若动点P从点B出发,以每秒3个单位的速度向右运动,点C以每秒1个单位的速度向左运动,点A以每秒2个单位的速度向右运动,三点同时出发,设运动时间为t秒,试判断4AP﹣CP的值是否会随着t的变化而变化?请说明理由.