山东省济南市历城区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关于地铁的图标中，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 生物学家发现一种病毒的直径约为0.00000013米，数字0.00000013用科学记轨法表示是（）

A、1.3×10^－5 B、0.13×10^－6 C、1.3×10^－7 D、1.3×10^－8

查看试题解析
3. 用下列长度的三根木棒首尾相接，能做成三角形框架的是（）

A、1，2，3 B、1，1，2 C、1，2，2 D、1，5，7

查看试题解析
4. 下列运算一定正确的是（）

A、（a³）²＝a⁶ B、（3a）²＝3a² C、a·a³＝a³ D、a⁶÷a²＝a³

查看试题解析
5. 已知点 $A$ 的坐标是 $(1 ， 2)$ ，则点 $A$ 关于 $y$ 轴的对称点的坐标是（）

A、 $(1 ， - 2)$ B、 $(- 1 ， 2)$ C、 $(- 1 ， - 2)$ D、 $(2 ， 1)$

查看试题解析
6. 下列说法中，正确的是（）

A、“从一副扑克牌（含大小王）中抽一张，恰好是红心A”是随机事件 B、“三角形两边之和大于第三边"是随机事件 C、“车辆到达路口，遇到红灯”是不可能事件 D、“任意画一个三角形，其内角和是360°”是必然事件

查看试题解析
7. 如图，直线l₁∥l₂ ， ∠1＝50°，∠2＝75°，则∠3＝（）

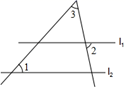A、55° B、60° C、65° D、70°

查看试题解析
8. 如图，用纸板挡住了三角形的一部分，小明根据所学知识很快就画出了一个与原来完全一样的三角形，他的依据是（）

A、ASA B、SAS C、AAS D、SSS

查看试题解析
9. 若点P（x，y）在第二象限，且点P到x轴的距离为3，到y轴的距离为2，则点P的坐标是（）

A、（－2，－3） B、（－2，3） C、（2，－3） D、（2，3）

查看试题解析
10. 小华同学喜欢锻炼，周六他先从家跑步到新华公园，在那里与同学打一会羽毛球后又步行回家，下面能反映小华离家距离 $y$ 与所用时间 $x$ 之间关系的图象是（）

A、 B、 C、 D、

查看试题解析
11. 如图，在△ABC中，BD平分∠ABC，E是BC的中点，过点E作BC的垂线交BD于点F，连结CF。若∠A=50°，∠ACF=40°，则∠CFD的度数为（）

A、30° B、45° C、55° D、60°

查看试题解析
12. 如图，在△ABC中，AB＝10，BC＝8，AC＝6，点O是三条角平分线的交点，则△BOC的BC边上的高是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 点P（m＋3，m－2）在x轴上，则m的值为；

查看试题解析
14. 如图，如果∠1＋∠2=280°，则∠3的度数是；

查看试题解析
15. 一个小球在如图所示的地板上自由滚动，并随机停在某块方砖上．如果每一块方砖除颜色外完全相同，那么小球最终停留在黑砖上的概率是．

查看试题解析
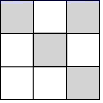16. 自变量x与因变量y的关系如图，当x每增加1时，y增加；

查看试题解析
17. 如图△ABC中，∠C＝90°，以顶点A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交干点P，作射线AP交边BC于点D，若CD＝4，BD＝5，AC＝12，则△ABD的面积是；

查看试题解析
18. 如图，长方形OACB在平面直角坐标系中，O是坐标原点，点A，B分别在x轴与y轴上，已知OA＝8，OB＝10．把长方形沿OP折叠，点B的对应点B₁恰好落在AC边上，则点P的坐标是．

查看试题解析

三、解答题

19. 计算下列各式

(1)、m⁸÷m²－（3m³）²＋2m²·m⁴；

(2)、（m²n＋2m³n－3m²n²）÷m²n．

(3)、 ${(a - 3)}^{2} - a (a + 7) - 9$

(4)、（－1）²⁰²¹＋（ $\frac{1}{2}$ ）^－2＋（3.14－π）⁰；

查看试题解析
20. 先化简，再求值：（a－2b）（a＋2b）－（a－2b）²＋8b，其中a＝－6，b＝ $\frac{1}{3}$ ．

查看试题解析
21. 如图，点B，E，C，F在一条直线上，∠B＝∠DEF，∠ACB＝∠F，BE＝CF．求证：∠A＝∠D．

查看试题解析
22. 在平面直角坐标系xOy中，△ABC的位置如图所示，点A，B，C都在格点上．

(1)、分别写出下列顶点的坐标：A；B；

(2)、请在图中画出△ABC关于y轴对称的图形△A′B′C′；

(3)、计算出△ABC的面积．

查看试题解析
23. 在一个口袋中只装有4个白球和11个红球，它们除颜色外完全相同．

(1)、事件“从口袋中随机摸出一个球是绿球”发生的概率是；

(2)、事件“从口袋中随机摸出一个球是白球”发生的概率是；

(3)、在袋中15球保持不变的情况下，摸到红球的概率为 $\frac{2}{3}$ ，则口袋中红球、白球各多少个？

查看试题解析
24. A、B两地相距60km，甲、乙两人从两地出发同向而行，甲先出发，图中l₁、l₂表示两人离A地的距离s（km）与时间t（h）的关系，请结合图象解答下列问题

(1)、表示乙离A地的距离与时间关系的图象是；（填 l₁或l₂），

(2)、甲的速度是 km/h，乙的速度是km/h；

(3)、甲出发多少小时两人恰好相距5 km？

查看试题解析
25. 如图，在 $△ A B C$ 中， $B C = 3$ ， $A C = 4$ ， $A B = 5$ ．动点 $P$ 从点 $B$ 出发沿射线 $B C$ 以每秒1单位的速度移动，设运动的时间为 $t$ ．

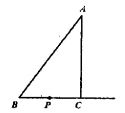(1)、求证 $△ A B C$ 为直角三角形．

(2)、若 $△ A B P$ 为直角三角形，求 $t$ 的值．

(3)、若 $△ A B P$ 为等腰三角形，求 $t$ 的值．

查看试题解析
26. 如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作等腰直角三角形ADE，∠ADE=∠AED=45°，∠DAE=90°，AD=AE．解答下列问题：

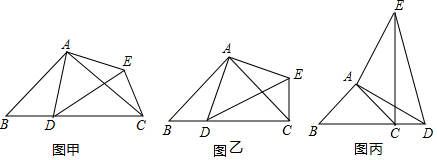(1)、如果AB=AC，∠BAC=90°，∠ABC=∠ACB=45°．
①当点D在线段BC上时（与点B不重合），如图乙，线段CE、BD之间的位置关系为 ▲ ，数量关系为 ▲ ．（不用证明）

②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

(2)、如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．
试探究：当△ABC满足一个什么条件时，CE⊥BD（点C、E重合除外）？画出相应的图形．

查看试题解析