山东省菏泽市定陶区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $A (3 ， - 5)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 人体的一种细胞的直径约为 $0.00000156$ 米，数据 $0.00000156$ 用科学记数法表示为（）

A、 $1.56 \times 10^{- 4}$ B、 $1.56 \times 10^{- 5}$ C、 $1.56 \times 10^{- 6}$ D、 $1.56 \times 10^{- 7}$

查看试题解析
3. 已知AB是半径为5的圆的一条弦，则AB的长不可能是（）

A、4 B、8 C、10 D、12

查看试题解析
4. 如果一个三角形的两边长分别为 $3$ 和 $6$ ，那么这个三角形第三边长可能是（）

A、 $2$ B、 $4$ C、 $9$ D、 $10$

查看试题解析
5. 若点P在第二象限内，且到x轴的距离是5，到y轴的距离是7，则点P的坐标是（）

A、（–7，5） B、（7，–5） C、（–5，7） D、（5，–7）

查看试题解析
6. 关于 $x$ ， $y$ 的方程 $a x - b y + 3 = 0$ 的解是 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ ， ${\begin{array}{l} x = - 1 \\ y = 1 \end{array}$ ，则 $a - 3 b$ 的值是（）

A、 $5$ B、 $- 5$ C、 $7$ D、 $- 7$

查看试题解析
7. 如图，直线l//m，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠1=25°，则∠2的度数为（）

A、20° B、25° C、30° D、35°

查看试题解析
8. 如图， $C E$ 是 $△ A B C$ 的外角 $∠ A C D$ 的平分线， $C E$ 交 $B A$ 的延长线于点 $E$ ， $∠ B = 35 °$ ， $∠ E = 25 °$ ，则 $∠ A C D$ 的度数为（）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
9. 多项式 $4 x^{2} + m x y + 25 y^{2}$ 是完全平方式，则 $m$ 的值是（）

A、20 B、10 C、10或－10 D、20或-20

查看试题解析
10. 如图，工人师傅做了一个长方形窗框ABCD ， E ， F ， G ， H分别是四条边上的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在（）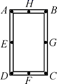

A、G ， H两点处 B、A ， C两点处 C、E ， G两点处 D、B ， F两点处

查看试题解析

二、填空题

11. 已知 $∠ A$ 是它的补角的 $4$ 倍，那么 $∠ A$ 度数为．

查看试题解析
12. 若 ${(a - 1)}^{2} + | b - 2 | = 0$ ，则以a、b为边长的等腰三角形的周长为．

查看试题解析
13. 课间操时，小颖、小浩的位置如图所示，小明对小浩说，如果我的位置用（0，0）表示，小颖的位置用（2，1）表示，那么小浩的位置可以表示成．

查看试题解析
14. 已知 $a - b = 5 ， a b = 3$ ，则 $a^{2} + b^{2} =$ .

查看试题解析
15. 计算 ${(- \frac{1}{2} x y^{3})}^{2} \cdot 6 x^{2} y$ 的结果是．

查看试题解析
16. 一个正多边形的每一个外角都等于 $36 °$ ，那么这个正多边形的内角和是．

查看试题解析
17. 如图，在 $△ A B C$ 中， $E$ 是 $B C$ 上的一点， $E C ＝ 2 B E$ ，点 $D$ 是 $A C$ 的中点，设 $△ A B C$ ， $△ A D F$ ， $△ B E F$ 的面积分别为 $S_{△ A B C}$ ， $S_{△ A D F}$ 和 $S_{△ B E F}$ ，且 $S_{△ A B C} ＝ 12$ ，则 $S_{△ A D F} - S_{△ B E F}$ = ．

查看试题解析
18. 已知点 $A (1 ， 0)$ 、 $B (0 ， 2)$ ，点P在 $x$ 轴上，且 $△ P A B$ 的面积为5，则点P的坐标为.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- \frac{1}{2})}^{- 3} - {(- 4)}^{- 1} \times 2 + {(2020 \times 8)}^{0}$

(2)、 $(2 x - 3) (3 + 2 x) + {(x - 2)}^{2}$

(3)、 $(4 a - 2) (2 a^{2} + a - 1) - {(3 a + 2)}^{2}$

查看试题解析
20. 分解因式：

(1)、 $m^{3} (x - 2) + m (2 - x)$

(2)、 $4 {(a - b)}^{2} + 1 + 4 (a - b)$

查看试题解析
21. 化简求值 ${(x - 2 y)}^{2} - 2 (x - y) (x + y) - 6 y^{2}$ ，其中 $x = {(- 3)}^{0} ， y = {(\frac{1}{2})}^{- 2}$

查看试题解析
22. 列方程组解应用题：六一儿童节，超市对甲、乙两种商品进行打折销售，其中甲种商品打八折，乙种商品打七五折，已知打折前，买 $6$ 件甲种商品和 $3$ 件乙种商品需 $600$ 元；打折后，买 $50$ 件甲种商品和 $40$ 件乙种商品需 $5200$ 元．求：打折前甲乙两种商品每件分别为多少元？

查看试题解析
23. 如图， $A B / / C D$ ， $B E$ 平分 $∠ A B C$ 交 $C D$ 于点 $D$ ， $∠ C D E = 150^{\circ}$ ，求 $∠ C$ 的度数.

查看试题解析
24. 已知点 $P (- 3 a - 4 ， 2 + a)$ ，解答下列各题：

(1)、若点 $P$ 在 $x$ 轴上，试求出点 $P$ 的坐标；

(2)、若 $Q (5 ， 8)$ ，且 $P Q ∥ y$ 轴，试求出点 $P$ 的坐标.

查看试题解析
25. 已知： $A (0 ， 1)$ ， $B (2 ， 0)$ ， $C (4 ， 3)$ ．

(1)、在直角坐标系中描出各点，画出 $△ A B C$ ．

(2)、求 $△ A B C$ 的面积；

(3)、已知 $P$ 为 $x$ 轴上一点且 $△ A B P$ 与 $△ A B C$ 的面积相等，求点 $P$ 的坐标．

查看试题解析
26.

(1)、如图①，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B＝30°，∠C＝50°.求∠DAE的度数；

(2)、如图②，已知AF平分∠BAC，交边BC于点E，延长AE至点F，过点F作FD⊥BC于点D，若∠B＝x°，∠C＝（x＋36）°.
①∠CAE＝ ▲ （含x的代数式表示）；

②求∠F的度数．

查看试题解析