河北省石家庄市新乐市2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 2018年4月18日，被誉为“中国天眼”的FAST望远镜首次发现的毫秒脉冲星得到国际认证．新发现的脉冲星自转周期为0.00519秒，将0.00519用科学记数法表示应为（）

A、5.19×10^﹣2 B、5.19×10^﹣3 C、5.19×10^﹣5 D、5.19×10^﹣6

查看试题解析
2. 计算2x²•（﹣3x³）的结果是（　　）

A、﹣6x⁵ B、6x⁵ C、﹣2x⁶ D、2x⁶

查看试题解析
3. 如图，直线c与直线a，b相交，且a∥b，∠1＝60°，则∠2的度数是（　　）

A、30° B、60° C、120° D、80°

查看试题解析
4. 如图，线段AD，AE， $A F$ 分别是 $△ A B C$ 的高线，角平分线，中线，比较线段 $A C$ ，AD，AE， $A F$ 的长短，其中最短的是（）

A、AF B、AE C、AC D、AD

查看试题解析
5. 如图，直线AB、CD相交于点O，下列描述：①∠1和∠2互为对顶角；②∠1和∠2互为邻补角；③∠1＝∠2，④ $∠ 1 = ∠ 3$ ，其中正确的是（）

A、①③ B、②④ C、②③ D、①④

查看试题解析
6. 若方程mx﹣2y＝3x＋4是关于x，y的二元一次方程，则m满足（）

A、m≠2 B、m≠0 C、m≠3 D、m≠4

查看试题解析
7. $x^{2} + k x + 16$ 是一个完全平方式，则k等于（）

A、 $\pm 8$ B、8 C、 $\pm 4$ D、4

查看试题解析
8. 如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C为（）

A、30° B、60° C、80° D、120°

查看试题解析
9. 如果a＞b，那么下列不等式成立的是（）

A、a－b ＜0 B、a－3＜b－3 C、－3a＜－3b D、 $\frac{1}{3} a < \frac{1}{3} b$

查看试题解析
10. 某县响应国家“退耕还林”号召，将一部分耕地改为林地，改还后，林地面积和耕地面积共有 $180 k m^{2}$ ，耕地面积是林地面积的 $25 %$ ，设改还后耕地面积为 $x k m^{2}$ ，林地面积为 $y k m^{2}$ ，则下列方程组中正确的是 $($ $)$

A、 ${\begin{array}{l} \overset{}{\begin{array}{l} x + y = 180 \\ x = 25 % y \end{array}} \end{array}$ B、 ${\begin{array}{l} \overset{}{\begin{array}{l} x + y = 180 \\ y = 25 % x \end{array}} \end{array}$ C、 ${\begin{array}{l} \overset{}{\begin{array}{l} x + y = 180 \\ x - y = 25 % \end{array}} \end{array}$ D、 ${\begin{array}{l} \overset{}{\begin{array}{l} x + y = 180 \\ y - x = 25 % \end{array}} \end{array}$

查看试题解析
11. 如果等腰三角形两边长是6和3，那么它的周长是( ）

A、15或12 B、9 C、12 D、15

查看试题解析
12. 为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间，小聪把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝80°， $∠ E C D = 110 °$ ，则∠E的度数是（）

A、30° B、40° C、60° D、70°

查看试题解析
13. 观察下列等式：
①3²﹣1²＝2×4

②5²﹣3²＝2×8

③7²﹣5²＝2×12……

那么第n（n为正整数）个等式为（）

A、n²﹣（n﹣2）²＝2×（2n﹣2） B、（n＋1）²﹣（n﹣1）²＝2×2n C、（2n）²﹣（2n﹣2）²＝2×（4n﹣2） D、（2n＋1）²﹣（2n﹣1）²＝2×4n

查看试题解析
14. 如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b）（如图1），将余下的部分拼成一个梯形（如图2），根据两个图形阴影部分面积的关系，可以得到个关于 $a ， b$ 的等式为（）

A、（a﹣b）²＝a²﹣2ab＋b² B、（a＋b）²＝a²＋2ab＋b² C、a²﹣b²＝（a＋b）（a﹣b） D、a²＋ab＝a（a＋b）

查看试题解析

二、填空题

15. 已知 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 是二元一次方程2x＋ay＝4的一个解，则a的值为．

查看试题解析
16. 写出不等式组 ${\begin{array}{l} x \geq - 1 ， \\ x < 1 \end{array}$ 的整数解为.

查看试题解析
17. 分解因式：m²n﹣4n＝.

查看试题解析
18. 如图，AB∥CD，一副三角尺按如图所示放置，∠AEG=20°，则∠HFD为°．

查看试题解析
19. 如果表示3xyz，表示﹣2a^bc^d ，则 × ＝．

查看试题解析
20. 在一次数学活动课上，老师让同学们借助一副三角板画平行线AB， $CD .$ 下面是小楠、小曼两位同学的作法：

老师说：“小楠、小曼的作法都符合题意 $.$ ”

请回答：小楠的作图依据是；

小曼的作图依据是．

查看试题解析

三、解答题

21. （﹣1）²⁰¹⁸﹣（π﹣3.14）⁰＋（ $\frac{1}{2}$ ）^﹣2

查看试题解析
22. 解不等式： $2 x + 1$ ≥ $3 x - 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
23. 解方程组 ${\begin{array}{l} x - y = 3 ， \\ 3 x + y = 5. \end{array}$

查看试题解析
24. 解不等式组： ${\begin{matrix} 4 x + 6 > x \\ \frac{x + 2}{3} \geq x \end{matrix}$ ．

查看试题解析
25. 计算： $3 a^{3} b^{2} \div a^{2} + b \cdot (a^{2} b - 3 a b)$

查看试题解析
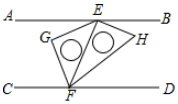
26. 完成下面的证明：
已知：如图，DE∥BC，∠DEB＝∠GFC，试说明 $B E // F G$ ．

证明：∵DE∥BC，

∴∠DEB＝   ▲   （    ）．

∵∠DEB＝∠GFC，

∴   ▲   ＝∠GFC（    ），

∴BE∥FG（    ）．

查看试题解析
27. 如图，在Rt△ABC中，∠ACB=90°，∠A=34°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．

(1)、求∠CBE的度数；

(2)、过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．

查看试题解析
28. 探究题
已知：如图1，AB∥CD，CD∥EF．求证：∠B＋∠BDF＋∠F＝360°．

老师要求学生在完成这道教材上的题目证明后，尝试对图形进行变式，继续做拓展探究

(1)、小颖首先完成了对这道题的证明，在证明过程中她用到了平行线的一条性质，小颖用到的平行线性质可能是．

(2)、接下来，小颖用《几何画板》对图形进行了变式，她先画了两条平行线AB、EF，然后在平行线间画了一点 $D$ ，连接BD，DF后，用鼠标拖动点 $D$ ，分别得到了图2、图3、图4，小颖发现图3正是上面题目的原型，于是她由上题的结论猜想到图2和图4中的 $∠ B$ 、 $∠ B D F$ 与 $∠ F$ 之间也可能存在着某种数量关系．于是她利用《几何画板》的度量和计算功能，找到了这三个角之间的数量关系．
请你在小颖操作探究的基础上，继续完成下面的问题：

①猜想图2中∠B、∠BDF与∠F之间的数量关系并加以证明；

②补全图4，直接写出∠B、∠BDF与∠F之间的数量关系： ▲ ．

查看试题解析
29. 某小区准备新建50个停车位，用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元；新建3个地上停车位和2个地下停车位共需1.3万元.

(1)、该小区新建1个地上停车位和1个地下停车位各需多少万元？

(2)、该小区的物业部门预计投资金额超过12万元而不超过13万元，那么共有哪几种建造停车位的方案？

查看试题解析