河北省保定市清苑区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 下面的图形是用数学家名字命名的,其中是轴对称图形的是( )A、
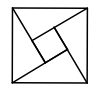 赵爽弦图
B、费马螺线
赵爽弦图
B、费马螺线  C、
C、 科克曲线
D、斐波那契螺旋线
科克曲线
D、斐波那契螺旋线  2. 下列运算正确的是( )A、 B、 C、 D、3. 已知 , , ,那么 , , 的大小关系为( )A、 B、 C、 D、4. 下列事件中,属于随机事件的是( ).A、13名同学中至少有两名同学的生日在同一个月 B、在只有白球的盒子里摸到黑球 C、经过交通信号灯的路口遇到红灯 D、用长为 , , 的三条线段能围成一个边长分别为 , , 的三角形5. 如图,点C在∠AOB的OB边上,用尺规作出了∠NCE=∠AOD,作图痕迹中,弧FG是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 已知 , , ,那么 , , 的大小关系为( )A、 B、 C、 D、4. 下列事件中,属于随机事件的是( ).A、13名同学中至少有两名同学的生日在同一个月 B、在只有白球的盒子里摸到黑球 C、经过交通信号灯的路口遇到红灯 D、用长为 , , 的三条线段能围成一个边长分别为 , , 的三角形5. 如图,点C在∠AOB的OB边上,用尺规作出了∠NCE=∠AOD,作图痕迹中,弧FG是( )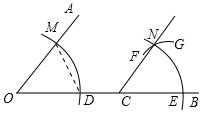 A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧6. 如图,下列条件中不能判定AB∥CD的是( )
A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧6. 如图,下列条件中不能判定AB∥CD的是( )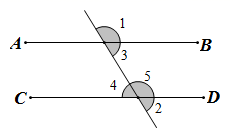 A、∠3=∠5 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠47. 若 ,则 的值为( )A、 B、 C、-3 D、8. 如图, 面积为1,第一次操作:分别延长 , , 至点 , , ,使 , , ,顺次连接 , , ,得到 ,则 的面积是( )
A、∠3=∠5 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠47. 若 ,则 的值为( )A、 B、 C、-3 D、8. 如图, 面积为1,第一次操作:分别延长 , , 至点 , , ,使 , , ,顺次连接 , , ,得到 ,则 的面积是( ) A、4 B、7 C、10 D、139. 张倩同学记录了某天一天的温度变化数据,如下表所示,则温度上升的时段是( )
A、4 B、7 C、10 D、139. 张倩同学记录了某天一天的温度变化数据,如下表所示,则温度上升的时段是( )时刻/时
温度
A、 时 B、 时 C、 时 D、 时10. 一个十字路口的交通信号灯,每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你拾头看信号灯时,出现绿灯的概率为( )A、 B、 C、 D、11. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3 =( ) A、150° B、135° C、120° D、90°12. 如图,线段 , 相交于点 ,若 ,为了直接使用“ ”判定 ,则应补充条件( )
A、150° B、135° C、120° D、90°12. 如图,线段 , 相交于点 ,若 ,为了直接使用“ ”判定 ,则应补充条件( ) A、 B、 C、 D、13. 某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额 ,与购书数量 之间的函数关系如何,同学们对此展开了讨论:
A、 B、 C、 D、13. 某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额 ,与购书数量 之间的函数关系如何,同学们对此展开了讨论:⑴小明说: 与 之间的函数关系为 ;
⑵小刚说: 与 之间的函数关系为 ;
⑶小聪说: 与 之间的函数关系在 时, ;在 时, ;
⑷小斌说;我认为用下面的列表法也能表示它们之间的关系.
购买量/本
1
2
3
4
…
9
10
11
12
…
付款金额/元
8
16
24
32
…
72
80
86.4
92.8
…
其中,表示函数关系正确的个数有( )
A、1个 B、2个 C、3个 D、4个14. 为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,
PB=12m,那么AB间的距离不可能是( ).
A、5m B、15m C、20m D、28m15. 如图,点 , 分别是 的边 , 上的点, , 相交于点 ,现给出下面两个结论,①当 , 是 的中线时, ;②当 , 是 的角平分线时, ,下列说法正确的是( ) A、只有①正确 B、只有②正确 C、①②都正确 D、①②都错误16. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )
A、只有①正确 B、只有②正确 C、①②都正确 D、①②都错误16. 如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( )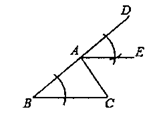 A、∠DAE=∠B B、∠EAC=∠C C、AE∥BC D、∠DAE=∠EAC
A、∠DAE=∠B B、∠EAC=∠C C、AE∥BC D、∠DAE=∠EAC二、填空题
-
17. 把0.00705写 ( , 为整数)的形式,则 为 .18. 如图, 要想说明 ,若以SAS为依据,还需添加的一个条件是 .
 19. 现有一张边长为 的大正方形卡片和三张边长为 的小正方形卡片 ,如图1;取出两张小正方形卡片放入大正方形卡片内拼成的图案如图2;再重新用三张小正方形卡片放入大正方形卡片内拼成的图案如图3,则图3中阴影部分的面积为(用含有 , 的代数式表示):已知图3中的阴影部分的面积比图2中的阴影部分的面积大 ,则小正方形卡片的面积是 .
19. 现有一张边长为 的大正方形卡片和三张边长为 的小正方形卡片 ,如图1;取出两张小正方形卡片放入大正方形卡片内拼成的图案如图2;再重新用三张小正方形卡片放入大正方形卡片内拼成的图案如图3,则图3中阴影部分的面积为(用含有 , 的代数式表示):已知图3中的阴影部分的面积比图2中的阴影部分的面积大 ,则小正方形卡片的面积是 .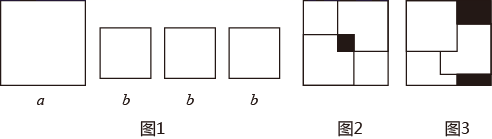
三、解答题
-
20. 计算:(1)、(2)、(3)、运用整式乘法公式进行计算:999×1001+1(4)、先化简,再求值: ,其中 , .21. 已知小明的家、体育场、青少年活动中心在同一条直线上,下图的图象反映的过程是:小明早上从家跑步去体育场,在那里锻炼了一阵后又走到青少年活动中心去看书画展览然后散步回家.图中 表示时间(单位是min), 表示到小明家的距离(单位是km).请根据相关信息,解答下列问题:
 (1)、填空:
(1)、填空:①小明在青少年活动中心停留了min;
②小明从家到体育场的速度为km/min;
③小明从青少年活动中心回家的平均速度为km/min;
④在全过程中,当小明距家的距离为0.6km时,他离开家的时间为min;
(2)、当 时,请直接写出 与 的关系式.22. 学习了平行线以后,小明想出了用纸折平行线的方法,他将一张如图1所示的纸片,其中 ,先按如图2所示的方法折叠,折痕为 ; ( 与 相交于点 )然后按如图3的方法折叠,折痕为 ( 与 落在一条直线上). (1)、在图2的折叠过程中,若 ,求 的度数(2)、如图3,小明认为在折叠过程中,产生的折痕 与 平行,请把小明的思考步骤补充完整.
(1)、在图2的折叠过程中,若 ,求 的度数(2)、如图3,小明认为在折叠过程中,产生的折痕 与 平行,请把小明的思考步骤补充完整.由折叠可知,
;
;
∵
∴ ;(① ▲ )
∴② ▲ =③ ▲ (等量代换)
∴ .(内错角相等,两直线平行)
23. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.(1)、先从袋子中取出 个红球( 且 为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.①若事件 为必然事件,则 的值为;
②若事件 为随机事件,则 的值为 .
(2)、先从袋子中取出 个红球,再放入 个一样的黄球并摇匀,经过多次试验,随机摸出一个黄球的频率在 附近摆动,求 的值.24. 如图1,已知 的三个顶点均在单位,长度为1的正方形网格中的格点上,请你按照要求完成以下问题: (1)、请直接写出图中 的面积为;(2)、动手操作与画图:请你根据所学全等与轴对称知识,在图2,图3,图4,图5的网格内完成以下设计轴对称图形的任务,要求如下:画出的三角形要与 全等,且它们的顶点都在格点上;画出的三角形与 关于某条直线成轴对称图形.
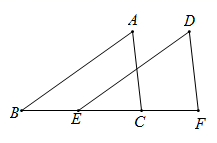
(1)、请直接写出图中 的面积为;(2)、动手操作与画图:请你根据所学全等与轴对称知识,在图2,图3,图4,图5的网格内完成以下设计轴对称图形的任务,要求如下:画出的三角形要与 全等,且它们的顶点都在格点上;画出的三角形与 关于某条直线成轴对称图形. 25. 某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
25. 某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米. (1)、河的宽度是米.(2)、请你说明他们做法的符合题意性.26. 如图,点 是 的中点,点 在线段 上(与 , 不重合);分别以 , 为边作正方形 和正方形 .设 , .
(1)、河的宽度是米.(2)、请你说明他们做法的符合题意性.26. 如图,点 是 的中点,点 在线段 上(与 , 不重合);分别以 , 为边作正方形 和正方形 .设 , . (1)、若正方形 与正方形 的面积之差为 ,用关于 , 的代数式表示 (结果化成最简形式);(2)、连接 , .请求出图中阴影部分的面积 ,(用关于 , 的代数式表示,结果化成最简形式).
(1)、若正方形 与正方形 的面积之差为 ,用关于 , 的代数式表示 (结果化成最简形式);(2)、连接 , .请求出图中阴影部分的面积 ,(用关于 , 的代数式表示,结果化成最简形式).