广东省深圳市南山区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 窗花是我国传统民间艺术,下列窗花中,是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为688纳米,1纳米=0.000 000 001米,则每个光量子的波长可用科学记数法表示为( )米A、 B、 C、 D、4. 下列说法正确的是( )A、“守株待兔”是必然事件 B、“概率为0.0001的事件”是不可能事件 C、“在一个只装有5个红球的袋中随机摸出1个球是红球”是必然事件 D、任意掷一枚质地均匀的硬币20次,正面向上的次数一定是10次5. 变量x与y之间的关系是 ,当 时,函数值y的值是( )A、2 B、3 C、11 D、126. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、87. 如图,用尺规作图作 的平分线 ,第一步是以 为圆心,任意长为半径画弧,分别交 于点 ;第二步是分别以 为圆心,以大于 长为半径画弧,两圆弧交于 点,连接 ,那么 为所作,则说明 的依据是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为688纳米,1纳米=0.000 000 001米,则每个光量子的波长可用科学记数法表示为( )米A、 B、 C、 D、4. 下列说法正确的是( )A、“守株待兔”是必然事件 B、“概率为0.0001的事件”是不可能事件 C、“在一个只装有5个红球的袋中随机摸出1个球是红球”是必然事件 D、任意掷一枚质地均匀的硬币20次,正面向上的次数一定是10次5. 变量x与y之间的关系是 ,当 时,函数值y的值是( )A、2 B、3 C、11 D、126. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、87. 如图,用尺规作图作 的平分线 ,第一步是以 为圆心,任意长为半径画弧,分别交 于点 ;第二步是分别以 为圆心,以大于 长为半径画弧,两圆弧交于 点,连接 ,那么 为所作,则说明 的依据是( )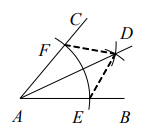 A、 B、 C、 D、8. 如图,直线 ,直线 与直线 相交于点 ,与直线 相交于点 , 于点 .若 ,则 ( )
A、 B、 C、 D、8. 如图,直线 ,直线 与直线 相交于点 ,与直线 相交于点 , 于点 .若 ,则 ( )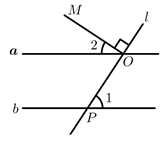 A、35° B、45° C、55° D、65°9. 某班共有45名同学,其中有3名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是( )A、0 B、 C、 D、110. 已知 , ,则 的值是( )A、64 B、52 C、50 D、28
A、35° B、45° C、55° D、65°9. 某班共有45名同学,其中有3名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是( )A、0 B、 C、 D、110. 已知 , ,则 的值是( )A、64 B、52 C、50 D、28二、填空题
-
11. 等腰三角形的一个角100°,它的另外两个角的度数分别为12. 一名老师带领x名学生到青青世界参观,已知成人票每张60元,学生票每张40元设门票的总费用为y元,则y与x的关系式为 .13. 如图,在 中, , 平分 ,过点 作 于 ,若 , 的周长为11,则 .
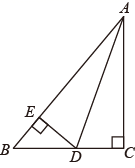 14. 如图,有两根钢条 、 ,在中点 处以小转轴连在一起做成工具(卡错),可测量工件内槽的宽.如果测量 ,那么工件内槽的宽 cm.
14. 如图,有两根钢条 、 ,在中点 处以小转轴连在一起做成工具(卡错),可测量工件内槽的宽.如果测量 ,那么工件内槽的宽 cm. 15. 如图,在 与 中, 与 相交于点 ,若 , , , , ,则 的度数为 .
15. 如图,在 与 中, 与 相交于点 ,若 , , , , ,则 的度数为 .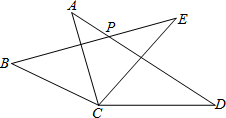 16. 阅读下面的推理过程,将空白部分补充完整.
16. 阅读下面的推理过程,将空白部分补充完整.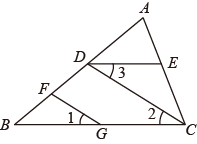
解:因为 (已知),
所以 ,
又因为 (已知),
所以 (等量代换).
所以 ()
所以 ( )
三、解答题
-
17. 计算:(1)、(2)、(3)、(4)、(5)、18. 先化简,再求值: ,其中19. 按要求完成作图:
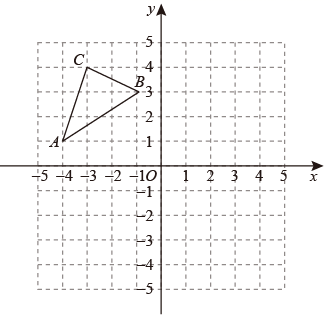 (1)、作出 关于 轴对称的图形 ;(2)、试求 的面积;20. 小明骑单车上学,当他骑了一段路时想要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)、作出 关于 轴对称的图形 ;(2)、试求 的面积;20. 小明骑单车上学,当他骑了一段路时想要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题: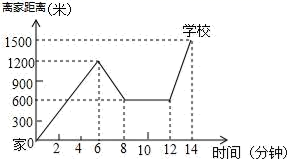 (1)、小明家到学校的路程是米,本次上学途中,小明一共行驶了米;(2)、小明在书店停留了 分钟,本次上学,小明一共用了分钟;(3)、在整个上学的途中那个时间段小明骑车速度最快,最快的速度是多少?21. 如图,在 中, , 的垂直平分线 交 、 于点 、 .
(1)、小明家到学校的路程是米,本次上学途中,小明一共行驶了米;(2)、小明在书店停留了 分钟,本次上学,小明一共用了分钟;(3)、在整个上学的途中那个时间段小明骑车速度最快,最快的速度是多少?21. 如图,在 中, , 的垂直平分线 交 、 于点 、 .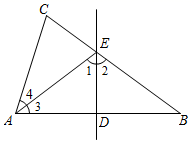 (1)、若 ,求 、 的度数;(2)、若 , ,求 的周长.22.(1)、探索发现:如图1,在 中,点 在边 上, 与 的面积分别记为 与 ,试判断 与 的数量关系,并说明理由.
(1)、若 ,求 、 的度数;(2)、若 , ,求 的周长.22.(1)、探索发现:如图1,在 中,点 在边 上, 与 的面积分别记为 与 ,试判断 与 的数量关系,并说明理由. (2)、阅读分析:小鹏遇到这样一个问题:如图,在 中, , ,射线 交 于点 ,点 、 在 上,且 ,试判断 、 、 三条线段之间的数量关系.小鹏利用一对全等三角形,经过推理使问题得以解决.图2中的 、 、 三条线段之间的数量关系为 , 并说明理由
(2)、阅读分析:小鹏遇到这样一个问题:如图,在 中, , ,射线 交 于点 ,点 、 在 上,且 ,试判断 、 、 三条线段之间的数量关系.小鹏利用一对全等三角形,经过推理使问题得以解决.图2中的 、 、 三条线段之间的数量关系为 , 并说明理由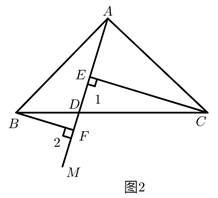 (3)、类比探究:如图3,在四边形 中, , 与 交于点 ,点 、 在射线 上,且 .
(3)、类比探究:如图3,在四边形 中, , 与 交于点 ,点 、 在射线 上,且 .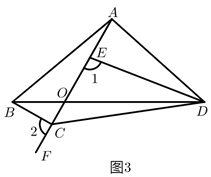
①全等的两个三角形为;
②若 , 的面积为2,直接写出 的面积: .