广东省深圳市光明区2020-2021学年七年级下学期数学期末试卷
试卷更新日期：2021-08-02 类型：期末考试
一、单选题
-
1. 下列汉字中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 某条信息一周内被转发0.0000218亿次，将数据0.0000218科学记数法表示为（ ）A、2.18×10﹣6 B、2.18×106 C、2.18×10﹣5 D、2.18×1053. 下列计算一定正确的是（ ）A、（﹣a3）2＝a5 B、a3÷a3＝0 C、（﹣a）3+a3＝1 D、a2﹣2a2＝﹣a24. 下列事件中，是必然事件的是（ ）A、明天北京新冠肺炎新增0人 B、车辆随机到达一个路口，遇到红灯 C、如果a2＝b2 ， 那么a＝b D、将花生油滴在水中，油会浮在水面上5. 如图是一个4×4的方格，若在这个方格内投掷飞镖，则飞镖恰好落在阴影部分的概率是（ ）
A、 B、 C、 D、6. 如图，已知点A、D、C、F在同一直线上，AB＝DE，添加下列条件后，仍不能判断△ABC≌△DEF的是（ ）
A、BC＝EF B、∠A＝∠EDF C、AB DE D、∠BCA＝∠EDF7. 如图，点P在直线l外，点A、B在直线l上，PA=4，PB＝7，则点P到直线l的距离可能是（ ）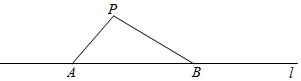
A、3 B、4 C、5 D、78. 如图，在下列条件中，能判断AB∥CD的是（ ）
A、∠1＝∠2 B、∠BAD＝∠BCD C、∠BAD＋∠ADC＝180° D、∠3＝∠49. 如图，a∥b，∠ABD的平分线交直线a于点C，CE⊥直线c于点E，∠1＝24°，则∠2的大小为（ ）
A、114° B、142° C、147° D、156°10. 如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P， ，PG AD交BC于F，交AB于G，① ；②S△PAC：S△PAB＝PC：PB；③BP垂直平分CE；④∠PCF＝∠CPF．其中正确的有（ ）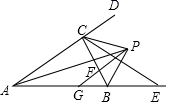
A、①②④ B、①③④ C、②③④ D、①③二、填空题
-
11. （﹣2）﹣1＝ ．12. 定义：如果一个数的平方等于﹣1，记为i2＝﹣1，这个数i叫做虚数单位，那么：（1+2i）（1﹣2i）＝ ．13. 如图，在△ABC中，∠B＝65°，∠C＝28°，分别以点A和点C为圆心，大于 画弧，两弧相交于点M，N，作直线MN，连接AD，则∠BAD的度数为 ．
14. 如图，在△ABC中，AD是BC边上的高，BE是AC边上的高，且AD、BE的交于点F，若BF＝AC，CD=6，BD＝8，则线段AF的长度为 ．
15. 如图，在△ABC中，E是AC的中点，AD，CF，BE交于一点G，BC＝3DC，S△GEC＝3，S△GBD＝8，则△ABC的面积是 ．
三、解答题
-
16. 计算：(1)、|﹣2|+（﹣2）2+（3.14﹣π）0﹣（ ）﹣1 ．(2)、（﹣2x）3÷x﹣（﹣x）2 ．17. 先化简，再求值：[（x﹣2y）（x+2y）﹣x（x﹣2y）]÷（2y），其中x＝1，y＝﹣2．18. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
(1)、在图中画出与△ABC关于直线l成轴对称的A1B1C1；(2)、△A1B1C1的面积是；(3)、利用网格线在直线上求作一点P，使得PA+PC最小，请在直线l上标出点P位置．19. 在一个口袋中只装有4个白球和6个红球，它们除颜色外完全相同.(1)、事件“从口袋中随机摸出一个球是绿球”发生的概率是；(2)、事件“从口袋中随机摸出一个球是红球”发生的概率是；(3)、现从口袋中取走若干个红球，并放入相同数量的白球，充分摇匀后，要使从口袋中随机摸出一个球是白球的概率是 ，求取走了多少个红球？20. 小明骑单车上学，当他骑了一段路时，想起要买某本书，买到书后继续去学校．以下是他本次上学所用的时间与离家距离的关系示意图．根据图中提供的信息回答下列问题：
(1)、小明家到学校的路程是米．(2)、本次上学途中，小明一共行驶了米．一共用了分钟．(3)、在整个上学的途中最快的速度是米/分．(4)、小明当出发分钟离家1200米．21. 填空：（将下面的推理过程及依据补充完整）已知：△ABC的高AD所在直线与高BE所在直线相交于点F，过点F作FG BC，交直线AB于点G．如图，且∠ABC＝45°．
求证：①△BDF≌△ADC；②FG+DC＝AD；
①证明：∵AD，BE为高
∴∠ADB＝∠BEC＝90°
∵∠ABC＝45°
∴∠BAD＝∠ ▲ ＝45°
∴AD＝ ▲ ；
∵∠BEC＝90°
∴∠CBE+∠C＝90°（ ）
又∵∠DAC+∠C＝90°
∴∠CBE＝∠DAC（ ）
在△FDB和△CDA中，
∵∠FDB＝∠CDA＝90°，
AD＝BD
∠CBE＝∠DAC
∴△FDB≌△CDA（ ）
②∵△FDB≌△CDA，
∴DF＝DC（ ）
∵GF BC
∴∠AGF＝∠ABC＝45°，（ ）
∴∠AGF＝∠ ▲ ，
∴FA＝FG；
∴FG+DC＝FA+DF＝AD．
22. 如图，AD BC，∠BAD的平分线交BC于点G．∠BCD＝90°．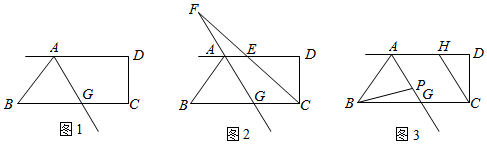
(1)、试说明：∠BAG＝∠BGA：(2)、如图2，∠BCD的平分线交AD于点E交射线GA于点F，①写出∠AFC，∠BAG的数量关系，并说明理由．
②若∠ABG＝55°，则∠AFC＝ ▲ ．
(3)、如图3，线段AG上有点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，则 的值是 ．