青海省西宁市大通回族土族自治县2020-2021学年高一下学期数学期末联考试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 不等式 的解集为( )A、 B、 C、 D、2. 有下列事件:
①在标准大气压下,水加热到 时会沸腾;
②实数的绝对值不小于零;
③某彩票中奖的概率为 ,则买100000张这种彩票一定能中奖.
其中必然事件是( )
A、② B、③ C、①②③ D、②③3. 在数列 中, ,则此数列最大项的值是A、103 B、 C、 D、1084. 已知一个三角形的三边长分别是2,3,4,如图是用秦九韶算法设计的一个求此三角形面积算法程序框图,则图中所缺的内容是( )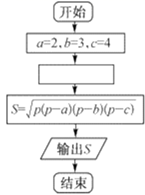 A、 B、 C、 D、5. 在 中,角 , , 所对的边分别为 , , ,有下列关系式:
A、 B、 C、 D、5. 在 中,角 , , 所对的边分别为 , , ,有下列关系式:① ;② ;③ .
其中一定成立的个数为( )
A、0 B、1 C、2 D、36. 将编号为001,002,003,…,500的500个产品,按编号从小到大的顺序均匀的分成若干组,采用系统抽样的方法抽取样本.若第一组抽取的编号是007,第二组抽取的编号是032,则样本中最大的编号应该是( )A、475 B、482 C、487 D、4927. 若 , 满足约束条件 ,则 的最小值为( )A、-3 B、3 C、-4 D、-18. 设数列 满足 ,且前 项和为 ,则 的值为( )A、 B、 C、 D、9. 下列说法不正确的是( )A、一个人打靶时连续射击两次,事件“至少有一次中靶”与事件“两次都不中靶”互斥 B、掷一枚均匀的硬币,如果连续抛掷1000次,那么第999次出现正面向上的概率是 C、若样本数据 , ,…, 的标准差为8,则数据 , ,…, 的标准差为16 D、取一根3米长的绳子,拉直后在任意位置剪断,那么剪得的两段的长都不小于1米的概率是10. 部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是:取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.如图所示,图1中有0个白色三角形,图2中有1个白色三角形,图3中有4个白色三角形,…,依此类推,可以判断图4中白色小三角形的个数为( ) A、10 B、12 C、13 D、1411. 如图,把 长的棒斜靠在石堤旁,棒的一端在离堤足 的地面上,另一端在沿堤向上 的地方,棒的上端恰好可以与堤的顶端平齐,则该石堤的高( ,结果保留两位小数)为( )
A、10 B、12 C、13 D、1411. 如图,把 长的棒斜靠在石堤旁,棒的一端在离堤足 的地面上,另一端在沿堤向上 的地方,棒的上端恰好可以与堤的顶端平齐,则该石堤的高( ,结果保留两位小数)为( )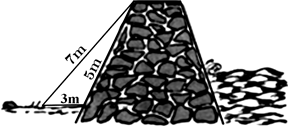 A、4.22m B、4.30m C、4.33m D、4.40m12. 有面积相等的四个游戏盘,如果投针落在阴影部分可中奖.小强希望中奖,那么他应选择的游戏盘为( )A、
A、4.22m B、4.30m C、4.33m D、4.40m12. 有面积相等的四个游戏盘,如果投针落在阴影部分可中奖.小强希望中奖,那么他应选择的游戏盘为( )A、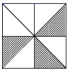 B、
B、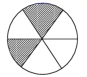 C、
C、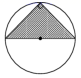 D、
D、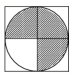
二、填空题
-
13. 已知正数 满足 ,则 的最小值为 .14. 如图,小明在山脚 测得山顶 的仰角为45°,在山脚 测得山顶 的仰角为30°,测得 , , 是钝角,已知山脚 和 , 在同一水平面上,则山的高度 为 .
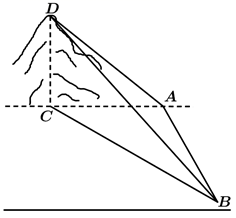 15. “关注夕阳、爱老敬老”——某协会从2015年开始每年向敬老院捐赠物资和现金.下表记录了第 年(2015年是第一年)与捐赠的现金 (万元)的对应数据,由此表中的数据得到了 关于 的线性回归方程为 ,则预测2021年捐赠的现金大约是万元.
15. “关注夕阳、爱老敬老”——某协会从2015年开始每年向敬老院捐赠物资和现金.下表记录了第 年(2015年是第一年)与捐赠的现金 (万元)的对应数据,由此表中的数据得到了 关于 的线性回归方程为 ,则预测2021年捐赠的现金大约是万元.3
4
5
6
2.5
3
4
4.5
16. 已知在 中,角 , , 的对边分别为 , , , , ,则 面积的最大值是 .三、解答题
-
17. 根据下列条件,求相应的未知数.(1)、在等差数列 中, , ,前 项和 ,求公差 及项数 ;(2)、在等比数列 中 , ,求 和公比 .18. 投掷一颗骰子2次,求投出的点数之和为10的概率.19. 某企业投资两个新型项目,投资新型项目 的投资额 (单位:十万元)与纯利润 (单位:万元)的关系式为 ,投资新型项目 的投资额 (单位:十万元)与纯利润 (单位:万元)的散点图如图所示.
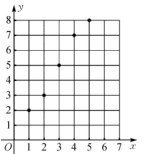 (1)、求 关于 的线性回归方程;(2)、若该企业有一笔50万元的资金用于投资 , 两个项目中的一个,为了收益最大化,应投资哪个项目?
(1)、求 关于 的线性回归方程;(2)、若该企业有一笔50万元的资金用于投资 , 两个项目中的一个,为了收益最大化,应投资哪个项目?附:回归直线 的斜率和截距的最小二乘估计分别为 , .
20. 已知 是公差为2的等差数列,且 , 是公比为3的等比数列,且 .(1)、求数列 , 的通项公式;(2)、令 ,求数列 的前 项和 .21. 新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从高中三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查. 已知该校高一年级共有学生660人,高三年级共有540人,抽取的样本中高二年级有50人. 下表是根据抽样调查情况得到的高二学生日睡眠时间(单位: )的频率分布表.分组
频数
频率
5
0.10
7
0.14
12
0.24
0.20
8
0.16
合计
50
1
(1)、求该校高二学生的总数;(2)、求频率分布表中实数 的值(3)、已知日睡眠时间在区间 内的5名高二学生中,有2名女生,3名男生,若从中任选3人进行面谈,求选中的3人恰好为两男一女的概率.22. 在 中角 , , 的对边分别为 , , , ,角 的平分线交 于点 , .(1)、求角 的大小.(2)、证明: .