辽宁省五校联考2020-2021学年高一下学期数学期末考试试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 已知zi+1=2i,则|z|=( )A、 B、 C、1 D、22. 点 是角 的终边上一点,则 ( )A、 B、 C、 D、3. 已知 为一条直线, 、 为两个不同的平面,则下列说法正确的是( )A、若 , ,则 B、若 , ,则 C、若 , ,则 D、若 , ,则4. 在 中,已知 为 上一点,且满足 ,则 ( )A、 B、 C、 D、5. 如图是一个近似扇形的鱼塘,其中 , 长为 .为方便投放饲料,欲在如图位置修建简易廊桥 ,其中 , .已知 时, ,则廊桥 的长度大约为( )
 A、 B、 C、 D、6. 在 中,已知 ,D是 边上一点,如图, ,则 ( )
A、 B、 C、 D、6. 在 中,已知 ,D是 边上一点,如图, ,则 ( ) A、 B、 C、2 D、37. 在轴截面顶角为直角的圆锥内,作一内接圆柱,若圆柱的表面积等于圆锥的侧面积,则圆锥的底面半径与圆柱的底面半径之比为( )A、 B、2 C、 D、48. 已知函数 是定义域为 的奇函数, ,且当 时, ,则下列结论正确的是( ).A、 B、 C、 D、
A、 B、 C、2 D、37. 在轴截面顶角为直角的圆锥内,作一内接圆柱,若圆柱的表面积等于圆锥的侧面积,则圆锥的底面半径与圆柱的底面半径之比为( )A、 B、2 C、 D、48. 已知函数 是定义域为 的奇函数, ,且当 时, ,则下列结论正确的是( ).A、 B、 C、 D、二、多选题
-
9. 已知向量 , ,则( )A、 B、向量 在向量 上的投影数量为 C、 与 的夹角余弦值为 D、若 ,则10. 已知函数 的部分图象如图所示,则下列说法正确的是( )
 A、 B、函数f(x)在 上单调递减 C、函数g(x)= cos2x的图象可由函数f(x)的图象向左平移 个单位得到 D、函数f(x)的图象关于( ,0)中心对称11. 在 中,角 , , 所对的边分别为 , , ,若 ,且 的面积为 ,则角 不可能是( )A、 B、 C、 D、12. 在菱形 中, , ,将菱形 沿对角线 折成大小为 的二面角 ,若折成的四面体 内接于球 ,则下列说法正确的是( ).A、四面体 的体积的最大值是 B、 的取值范围是 C、四面体 的表面积的最大值是 D、当 时,球 的体积为
A、 B、函数f(x)在 上单调递减 C、函数g(x)= cos2x的图象可由函数f(x)的图象向左平移 个单位得到 D、函数f(x)的图象关于( ,0)中心对称11. 在 中,角 , , 所对的边分别为 , , ,若 ,且 的面积为 ,则角 不可能是( )A、 B、 C、 D、12. 在菱形 中, , ,将菱形 沿对角线 折成大小为 的二面角 ,若折成的四面体 内接于球 ,则下列说法正确的是( ).A、四面体 的体积的最大值是 B、 的取值范围是 C、四面体 的表面积的最大值是 D、当 时,球 的体积为三、填空题
-
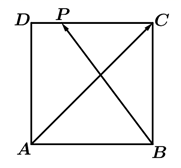
13. 设 是虚数单位,复数 为纯虚数,则实数 .14. 如图,正方形 的边长为2, 是线段 上的动点(含端点),则 的取值范围是 .
 15. 已知 的内角 , , 所对的边分别为 , , ,且 , ,则 .16. 柏拉图多面体,是指严格对称,结构等价的正多面体.由于太完美,因此数量很少,只有正四、六、八、十二、二十面体五种.如果用边数不同的正多边形来构造接近圆球、比较完美的多面体,那么数量会多一些,用两种或两种以上的正多边形构建的凸多面体虽不是正多面体但有些类似,这样的多面体叫做半正多面体.古希腊数学家物理学家阿基米德对这些正多面体进行研究并发现了13种半正多面体(后人称为“阿基米德多面体”).现在正四面体上将四个角各截去一角,形成最简单的阿基米德家族种的一个,又名截角四面体.设原正四面体的棱长为6,则所得的截角四面体的表面积为 , 该截角四面体的体积为 .
15. 已知 的内角 , , 所对的边分别为 , , ,且 , ,则 .16. 柏拉图多面体,是指严格对称,结构等价的正多面体.由于太完美,因此数量很少,只有正四、六、八、十二、二十面体五种.如果用边数不同的正多边形来构造接近圆球、比较完美的多面体,那么数量会多一些,用两种或两种以上的正多边形构建的凸多面体虽不是正多面体但有些类似,这样的多面体叫做半正多面体.古希腊数学家物理学家阿基米德对这些正多面体进行研究并发现了13种半正多面体(后人称为“阿基米德多面体”).现在正四面体上将四个角各截去一角,形成最简单的阿基米德家族种的一个,又名截角四面体.设原正四面体的棱长为6,则所得的截角四面体的表面积为 , 该截角四面体的体积为 .
四、解答题
-
17. 已知复数 , ( ,i是虚数单位).(1)、若 在复平面内对应的点落在第一象限,求实数a的取值范围;(2)、若虚数 是实系数一元二次方程 的根,求实数m的值.18. 已知非零向量 , 满足 ,且 .(1)、求 与 的夹角;(2)、若 ,求 .19. 在①2asinC=ctanA;②2acosB=2c﹣b;③ ;这三个条件中任选一个,补充在下面问题中,并作答.
在 中,内角A,B,C所对的边分别是a,b,c,已知____.
(1)、求A的值;(2)、若 面积为 ,周长为5,求a的值.20. 如图,在多面体 中,四边形 和 均为直角梯形, , ,且 , . (1)、求证: 平面 ,(2)、求点 到平面 的距离.
(1)、求证: 平面 ,(2)、求点 到平面 的距离.
