河南省焦作市普通高中2021-2022学年高一下学期(新高二)数学定位考试试卷
试卷更新日期:2021-08-02 类型:期末考试
一、单选题
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. ( )A、 B、 C、 D、3. 已知 ,则坐标原点 到直线 的距离小于 的概率为( )A、 B、 C、 D、4. 已知 , , ,则( )A、 B、 C、 D、5. 一个几何体的三视图如图所示,其中俯视图是圆的一部分,则该几何体的体积为( )
 A、 B、 C、 D、6. 某健康研究机构调查了100位居民的日平均睡眠时间(单位:时),统计数据制成频率分布直方图,如图所示,则估计这100位居民的日平均睡眠时间的中位数约为( )
A、 B、 C、 D、6. 某健康研究机构调查了100位居民的日平均睡眠时间(单位:时),统计数据制成频率分布直方图,如图所示,则估计这100位居民的日平均睡眠时间的中位数约为( ) A、6.7 B、6.8 C、6.9 D、77. 已知 ,且 , ,则 ( )A、1 B、7 C、1或7 D、2或68. 执行如图所示的程序框图,则输出的 ( )
A、6.7 B、6.8 C、6.9 D、77. 已知 ,且 , ,则 ( )A、1 B、7 C、1或7 D、2或68. 执行如图所示的程序框图,则输出的 ( )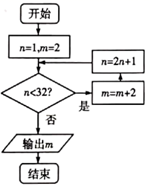 A、10 B、12 C、14 D、169. 如图所示, 是 内任意一点, 的对角线交于点 ,则 ( )
A、10 B、12 C、14 D、169. 如图所示, 是 内任意一点, 的对角线交于点 ,则 ( ) A、 B、 C、 D、10. 在四棱锥 中,底面 为平行四边形, 是 的中点,若在棱 上存在一点 ,使得 平面 ,则 ( )A、3 B、2 C、 D、111. 已知函数 在区间 上单调递减,则实数 的取值范围是( )A、 B、 C、 D、12. 如图所示, 、 为函数 的图象与正六边形的两个公共点(点 在 轴上),正六边形与 轴的一个交点为 , 的图象与 轴的交点为 ,其中正六边形关于坐标轴对称,且边长为 ,则下列结论中正确的个数为( )
A、 B、 C、 D、10. 在四棱锥 中,底面 为平行四边形, 是 的中点,若在棱 上存在一点 ,使得 平面 ,则 ( )A、3 B、2 C、 D、111. 已知函数 在区间 上单调递减,则实数 的取值范围是( )A、 B、 C、 D、12. 如图所示, 、 为函数 的图象与正六边形的两个公共点(点 在 轴上),正六边形与 轴的一个交点为 , 的图象与 轴的交点为 ,其中正六边形关于坐标轴对称,且边长为 ,则下列结论中正确的个数为( )①函数 的最小正周期为 ;②函数 的图象关于直线 对称;
③函数 的单调增区间为 , ;④ .
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 已知直线 : 与直线 : 平行,则 .14. 某单位年龄(单位:岁)在 的员工有40人,年龄在 的员工有60人,年龄在 的员工有20人.现准备用分层抽样的方法从这些员工中选拔18人代表单位参加技术比武活动,则选拔出的员工中,年龄小于50岁的员工人数为 .15. 某汽车制造厂生产一款新的汽车,今年前5个月的产量如下:
月份
1
2
3
4
5
汽车产量 (千辆)
2
5
7
8
若根据表中提供的数据,求出 关于 的线性回归方程为 ,那么表中 的值为 .
16. 如图所示,在平面四边形 中, , , , 与 交于点 ,若 , ( 为常数),则 .
三、解答题
-
17. 已知函数 且 是奇函数.(1)、求 的值;(2)、令函数 ,若关于 的方程 在 上有解,求实数 的取值范围.18. 已知向量 , , ,且 .(1)、求实数 的值;(2)、求 与 夹角的余弦值.19. 为了回馈消费者,某商场准备在假期举行优惠活动,据统计,消费者在该商场的消费金额都不超过800元,活动策划人员准备了两种优惠方案.
方案一:消费金额满300元减50元,满600元减120元,只取最高优惠,不重复减免;
方案二:消费金额满400元享受8折优惠.
活动策划人员从电脑中存储的最近的消费记录中随机抽取了100位消费者的消费金额(单位:元),整理得到如下频数分布表:
消费金额(元)
频数
8
14
22
20
12
10
8
6
(1)、分别估计两种方案下消费者参与优惠活动的概率;(2)、在消费金额的频数分布表中取每组中间值作为代表,从全部消费者享受的优惠平均值角度分析哪种方案的优惠力度更大.