浙江省宁波市镇海区七校2020-2021学年七年级下学期数学期末联考试卷

试卷更新日期：2021-07-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列选项中能由下图平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 端午节放假后，赵老师从七年级650名学生中随机抽查了其中50名学生的数学作业，发现有5名学生的作业不合格，下面判断正确的是（）

A、赵老师采用全面调查方式 B、个体是每名学生 C、样本容量是650 D、该七年级学生约有65名学生的作业不合格

查看试题解析
3. N95型口罩可阻隔直径为0.0000003米的飞沫，用科学记数法可将数0.0000003表示为（）

A、 $30 \times 10^{- 8}$ B、 $3 \times 10^{- 7}$ C、 $0.3 \times 10^{- 6}$ D、 $3 \times 10^{- 6}$

查看试题解析
4. 下列方程是二元一次方程的是（）

A、y＝x B、x＋ $\frac{1}{y}$ ＝2 C、xy＝6 D、x﹣y＝z﹣5

查看试题解析
5. 若 $(x + 1) (x^{2} - 5 a x + a)$ 的乘积中不含 $x^{2}$ 项，则 $a$ 的值为（）

A、5 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、-5

查看试题解析
6. 下列各式中，能用完全平方公式分解因式的是（）

A、 $4 x^{2} - 1$ B、 $4 x^{2} + 4 x - 1$ C、 $x^{2} - x y + y^{2}$ D、 $x^{2} - x + \frac{1}{4}$

查看试题解析
7. 能使分式 $\frac{4 x + 7}{2 x - 3}$ 值为整数的整数x有（）个．

A、1 B、2 C、3 D、.4

查看试题解析
8. 如图，一辆超市购物车放置在水平地面上，其侧面四边形ABCD与地面某条水平线l在同一平面内，且AB∥l，若∠A=93°，∠D=111°，则直线CD与l所夹锐角的度数为（）

A、15° B、18° C、21° D、24°

查看试题解析
9. 某煤厂原计划x天生产120吨煤，实际每天比原计划多生产3吨，因此提前2天完成生产任务，则根据题意，得方程（）

A、 $\frac{120}{x - 2}$ ＝ $\frac{120}{x}$ ﹣3 B、 $\frac{120}{x}$ ＝ $\frac{120}{x + 2}$ ﹣3 C、 $\frac{120}{x}$ ＝ $\frac{120}{x - 2}$ ﹣3 D、 $\frac{120}{x + 2}$ ＝ $\frac{120}{x}$ ﹣3

查看试题解析
10. 将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内（相同纸片之间不重叠），其中AB＝a.小明发现：通过边长的平移和转化，阴影部分⑤的周长与正方形①的边长有关，那么阴影部分⑥与阴影部分⑤的周长之差与正方形（）（填编号）的边长有关.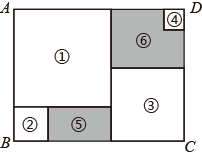

A、① B、② C、③ D、④

查看试题解析

二、填空题

11. 计算 $- 3 a \cdot (2 b)$ ＝．

查看试题解析
12. 若分式 $\frac{x - 3}{x + 2}$ 有意义，则x的取值范围是.

查看试题解析
13. 若二次三项式x²﹣kx＋16是一个完全平方式，则k的值是.

查看试题解析
14. 统计得到的一组数据有80个，其中最大值为139，最小值为49，取组距为10，可分成组.

查看试题解析
15. 已知实数a²＋b²＝7，a＋b＝3，则（a﹣2）（b﹣2）＝.

查看试题解析
16.
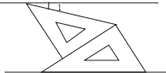
如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是．

查看试题解析
17. 若关于x的方程 $\frac{3}{x} + \frac{6}{x - 1} = \frac{m x + m}{x^{2} - x}$ 无解，则 $m =$ 。

查看试题解析
18. 将一张长为12.6cm，宽为acm的长方形纸片按图折叠出一个正方形并剪下，称为第一次操作；将余下的长方形纸片再次折叠出一个正方形并剪下，称为第二次操作…如此操作下去，若每一次剪下后的长方形纸片只能折出一个正方形，当第五次操作后，剩下图形的长与宽之比为2：1，则a的值为.

查看试题解析

三、解答题

19.

(1)、计算：
① ${(- 3)}^{2} + {(\frac{1}{2})}^{- 3} - 2019^{0}$ ；

② ${(2 m - 3)}^{2} - (m + 1) (m - 1) - 3 m (m - 4)$ ；

(2)、分解因式：
①4a⁴﹣36a²；

② $\frac{1}{3}$ x²﹣2xy＋3y²

查看试题解析
20. 先化简再求值： $\frac{x^{2} - 4}{x^{2} + 4 x + 4}$ ÷（ $\frac{2 x - 4}{x + 2}$ ﹣x＋2），其中x可在﹣2，0，3三个数中任选一个合适的数.

查看试题解析
21. “中国梦”是中华民族每一个人的梦，也是每一个中小学生的梦，各中小学开展经典诵读活动，无疑是“中国梦”教育这一宏大乐章里的响亮音符，学校在经典诵读活动中，对全校学生用A、B、C、D四个等级进行评价，现从中抽取若干个学生进行调查，绘制出了两幅不完整的统计图，请你根据图中信息解答下列问题：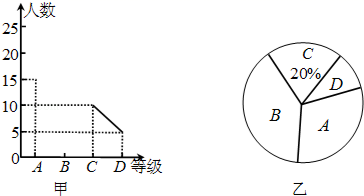

(1)、共抽取了多少个学生进行调查？

(2)、将图甲中的折线统计图补充完整.

(3)、求出图乙中B等级所占圆心角的度数.

查看试题解析
22. 阅读下列材料：对于多项式x²＋x﹣2，如果我们把x＝1代入此多项式，发现x²＋x﹣2的值为0，这时可以确定多项式中有因式（x﹣1）；同理，可以确定多项式中有另一个因式（x＋2），于是我们可以得到：x²＋x﹣2＝（x﹣1）（x＋2）.又如：对于多项式2x²﹣3x﹣2，发现当x＝2时，2x²﹣3x﹣2的值为0，则多项式2x²﹣3x﹣2有一个因式（x﹣2），我们可以设2x²﹣3x﹣2＝（x﹣2）（mx＋n），解得m＝2，n＝1，于是我们可以得到：2x²﹣3x﹣2＝（x﹣2）（2x＋1）.
请你根据以上材料，解答以下问题：

(1)、当x＝时，多项式8x²﹣x﹣7的值为0，所以多项式8x²﹣x﹣7有因式，从而因式分解8x²﹣x﹣7＝；

(2)、以上这种因式分解的方法叫试根法，常用来分解一些比较复杂的多项式，请你尝试用试根法分解多项式：
①3x²＋11x＋10；

②x³﹣21x＋20

查看试题解析
23. 目前，新型冠状病毒在我国虽可控可防，但不可松懈.某校欲购置规格分别为 $300 m l$ 和 $500 m l$ 的甲、乙两种免洗手消毒液若干瓶.已知购买2瓶甲和1瓶乙免洗手消毒液需要55元，购买3瓶甲和4瓶乙免洗手消毒液需要145元.

(1)、求甲、乙两种免洗手消毒液的单价.

(2)、该校在校师生共1000人，平均每人每天都需使用10mL的免洗手消毒液，若校方采购甲、乙两种免洗手消毒液共花费5000元，则这批消毒液可使用多少天?

(3)、为节约成本，该校购买散装免洗手消毒液进行分装.现需将9.6L的免洗手消毒液全部装入最大容量分别为 $300 m l$ 和 $500 m l$ 的两种空瓶中(每瓶均装满)，若分装时平均每瓶需损耗 $20 m l$ ，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量.

查看试题解析
24. 已知直线AB∥CD，

(1)、如图1，直接写出∠BME、∠E、∠END的数量关系为；

(2)、如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；

(3)、如图3，∠ABM= $\frac{1}{n}$ ∠MBE，∠CDN= $\frac{1}{n}$ ∠NDE，直线MB、ND交于点F，则 $\frac{∠ F}{∠ E}$ =.

查看试题解析