浙江省宁波市鄞州区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下面调查中，适合全面调查的是（）

A、我市初中生的身高情况 B、乘坐地铁的安全检查 C、东钱湖景区全年的游客流量 D、某品牌水笔笔芯的使用寿命

查看试题解析
2. 古语有云：“水滴石穿”，若水珠不断滴在一块石头上，经过40年，石头上会形成一个深为 $0.0000048 cm$ 的小洞.数0.0000048用科学记数法表示为（）

A、 $4.8 \times 10^{5}$ B、 $4.8 \times 10^{- 6}$ C、 $4.8 \times 10^{- 7}$ D、 $48 \times 10^{- 7}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{5} - a^{2} = a^{3}$ B、 $a^{10} \div a^{2} = a^{5}$ C、 ${(a + 3)}^{2} = a^{2} + 9$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
4. 下列等式从左到右的变形，属于因式分解是（）

A、 $a (4 - y^{2}) = 4 a - a y^{2}$ B、 $x^{2} + 3 x - 1 = x (x + 3) - 1$ C、 $4 x^{2} - 12 x y + 9 y^{2} = {(2 x - 3 y)}^{2}$ D、 $x^{2} + y^{2} = {(x + y)}^{2} - 2 x y$

查看试题解析
5. 要使分式 $\frac{1}{x - 4}$ 有意义，x的取值范围满足（）

A、 $x \neq 4$ B、 $x = 4$ C、 $x > 4$ D、 $x < 4$

查看试题解析
6. 如图， $△ A B C$ 沿直线m向右平移 $2 cm$ ，得到 $△ D E F$ ，下列说法错误的是（）

A、 $A C // D F$ B、 $A B = D E$ C、 $C F = 2 cm$ D、 $D E = 2 cm$

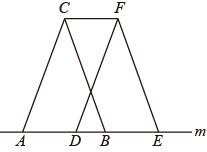查看试题解析
7. 如图，直线a、b被直线l所截，且 $a // b$ ，若 $∠ 1 = 60 °$ ，则 $∠ 2$ 的度数是（）

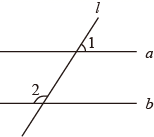A、140° B、120° C、60° D、30°

查看试题解析
8. 《九章算术》中记录的一道题译为白话文是：把一份文件用慢马送到900里外的城市，需要的时间比规定时间多1天，如果用快马送，所需的时间比规定时间少3天，已知快马的速度是慢马的2倍，求规定的时间.设规定时间为x天，则可列方程为（）

A、 $\frac{900}{x + 1} \times 2 = \frac{900}{x - 3}$ B、 $\frac{900}{x + 1} = \frac{900^{2}}{x - 3} \times 2$ C、 $\frac{900}{x - 1} \times 2 = \frac{900}{x + 3}$ D、 $\frac{900}{x + 1} = \frac{900}{x + 3} \times 2$

查看试题解析
9. 若关于x，y的二元一次方程组 ${\begin{array}{l} x + 2 y = 6 k \\ x - y = 3 k \end{array}$ 的解，也是二元一次方程 $2 x + y = 3$ 的解，则k的值为（）

A、 $- 3$ B、3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
10. 如图，正方形ABCD和长方形DEFG的面积相等，且四边形AEFH也为正方形.欧几里得在《几何原本》中利用该图得到了：AH²=AB×BH.设AB=a，BH=b.若ab=45，则图中阴影部分的周长为（）

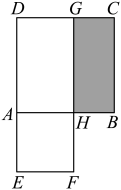A、25 B、26 C、28 D、30

查看试题解析

二、填空题

11. 计算：2^﹣¹= ．

查看试题解析
12. 因式分解： $a^{2} - 2 a =$ .

查看试题解析
13. 将方程4x+3y=6变形成用y的代数式表示x，则x= ．

查看试题解析
14. 将50个数据分成3组，其中第1组与第3组的频率之和是0.7，则第2组的频数是.

查看试题解析
15. 已知3a-b=0，则分式 $\frac{a + b}{b}$ 的值为

查看试题解析
16. 将一副三角板按如图摆放，已知直线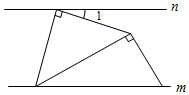 $m // n$ ，则 $∠ 1$ 的度数为.

查看试题解析
17. 若关于x的分式方程 $\frac{2 x + 1}{x - 3} = 1 - \frac{a}{3 - x}$ 有增根，则a的值为.

查看试题解析
18. 若一个整数能表示成 $a^{2} + b^{2}$ （a、b为整数）的形式，则称这个数为“完美数”，例如：因为 $5 = 2^{2} + 1$ ，所以5是一个完美数.已知 $M = x^{2} + 4 y^{2} + 4 x - 12 y + k$ （x、y是整数，k是常数），要使M为“完美数”，则k的值为.

查看试题解析

三、解答题

19. 因式分解：

(1)、 $a^{2} - 4 b^{2}$

(2)、 $- x^{2} + 6 x y - 9 y^{2}$

查看试题解析
20. 先化简，后求值：

(1)、 $x (4 x + 2) - (2 x - 1) (2 x + 1)$ ，其中 $x = - 3$

(2)、 $\frac{a - 1}{a^{2} - 4} \div (1 - \frac{3}{a + 2})$ 先化简，再选择一个合适的数作为 $a$ 的值代入求值.

查看试题解析
21. 解下列方程（组）：

(1)、 ${\begin{array}{l} 2 x + y = 3 \\ 4 x - 3 y = 11 \end{array}$

(2)、 $\frac{x}{x - 3} - 4 = \frac{3}{3 - x}$

查看试题解析
22. 乐善好施、扶贫帮困是中华民族的传统美德，在建党100周年之际，某校举行了一次爱心捐款活动.为了解捐款情况，小亮抽取了部分同学的捐款数额，并将统计结果绘制成如下统计图.
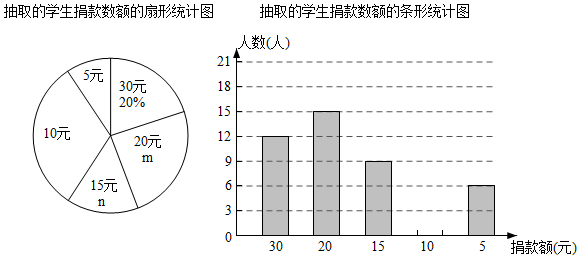
请根据图中信息回答问题：

(1)、求m、n的值.

(2)、补全条形统计图.

(3)、在扇形统计图中，表示5元的扇形的圆心角是多少度？

(4)、该校共有1200名学生，试估计全校捐款额不少于15元的学生人数.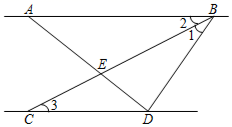

查看试题解析
23. 如图，已知 $B C$ 平分 $∠ A B D$ 交 $A D$ 于点E， $∠ 1 = ∠ 3$ .

(1)、证明： $A B // C D$

(2)、若 $A D ⊥ B D$ 于点D， $∠ C D A = 34 °$ ，求 $∠ 3$ 的度数.

查看试题解析
24. 目前，新型冠状病毒在我国虽可控可防，但不可松懈某校欲购置规格分别为 $300 ml$ 和 $500 ml$ 的甲、乙两种免洗手消毒液若干瓶，已知购买1瓶甲和1瓶乙免洗手消毒液需要32元，购5瓶甲和3瓶乙免洗手消毒液需要120元.

(1)、求甲、乙两种免洗手消毒液的单价.

(2)、该校在校师生共1000人，平均每人每天都需使用 $10 ml$ 的免洗手消毒液，若校方采购甲、乙两免洗手消毒液共花费4000元，则这批消毒液可使用多少天？

(3)、为节约成本，该校购买散装免洗手消毒液进行分装，现需将 $9.6 L$ 的免洗手消毒液全部装入最大容量分别为 $300 ml$ 和 $500 ml$ 的两种空瓶中（每瓶均装满），若分装时平均每瓶需损耗 $20 ml$ ，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量.

查看试题解析