浙江省宁波市北仑区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-07-30 类型:期末考试
一、单选题
-
1. 是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )A、 B、 C、 D、2. 若分式 的值为0,则 的值为( )A、-5 B、5 C、-5和5 D、无法确定3. 下列调查中,适合用抽样调查的是( )A、防疫期间对进入校园的人员进行体温检测 B、对乘坐高铁的乘客进行安检 C、调查一批防疫口罩的质量情况 D、对新研发导弹的零部件进行检查4. 下列运算正确的是( )A、 B、 C、 D、5. 如图, , , 被直线 所截,若 ,则 ( )
 A、50° B、60° C、70° D、80°6. 整式n2﹣1与n2+n的公因式是( )A、n B、n2 C、n+1 D、n﹣17. 明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问都多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )A、 B、 C、 D、8. 若 , .则 的值为( )A、 B、4 C、 D、29. 若 ,则使 最接近 的正整数 是( )A、3 B、4 C、5 D、610. 如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A、50° B、60° C、70° D、80°6. 整式n2﹣1与n2+n的公因式是( )A、n B、n2 C、n+1 D、n﹣17. 明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问都多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )A、 B、 C、 D、8. 若 , .则 的值为( )A、 B、4 C、 D、29. 若 ,则使 最接近 的正整数 是( )A、3 B、4 C、5 D、610. 如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( ) A、①② B、②③ C、①③ D、①②③
A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 要使分式 有意义,则 x 的取值范围是.12. 分解因式: .13. 如图,直线 被 所截,下列条件:① ;② ;③ ,其中能判断 的一个条件是.
 14. 某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有人.
14. 某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有人. 15. 小慧去花店买鲜花,若买6支玫瑰和4支百合,则她所带的钱还剩下11元;若买4支玫瑰和6支百合,则她所带的钱还缺5元.若只买10支玫瑰,则她所带的钱还剩下元.16. 在一副三角尺中∠BPA=45°,∠CPD=60°,∠B=∠C=90°,将它们按如图所示摆放在量角器上,边PD与量角器的0°刻度线重合,边AP与量角器的180°刻度线重合.将三角尺PCD绕点P以每秒3°的速度逆时针旋转,同时三角尺ABP绕点P以每秒2°的速度顺时针旋转,当三角尺PCD的PC边与180°刻度线重合时两块三角尺都停止运动,则当运动时间t =秒时,两块三角尺有一组边平行.
15. 小慧去花店买鲜花,若买6支玫瑰和4支百合,则她所带的钱还剩下11元;若买4支玫瑰和6支百合,则她所带的钱还缺5元.若只买10支玫瑰,则她所带的钱还剩下元.16. 在一副三角尺中∠BPA=45°,∠CPD=60°,∠B=∠C=90°,将它们按如图所示摆放在量角器上,边PD与量角器的0°刻度线重合,边AP与量角器的180°刻度线重合.将三角尺PCD绕点P以每秒3°的速度逆时针旋转,同时三角尺ABP绕点P以每秒2°的速度顺时针旋转,当三角尺PCD的PC边与180°刻度线重合时两块三角尺都停止运动,则当运动时间t =秒时,两块三角尺有一组边平行.

三、解答题
-
17. 计算:(1)、 ;(2)、先化简,后求值: ,其中 .18. 解方程:(1)、 ;(2)、 .19. 教育部颁发的《中小学教育惩戒规则(试行)》并从2021年3月1日起实行,某校随机抽取该校部分家长,按四个类别: 表示“非常支持”, 表示“支持”, 表示“不关心”, 表示“不支持”,调查他们对该规则态度的情况,将结果绘制成如下两幅不完整的统计图,
根据图中提供的信息,解决下列问题:
 (1)、这次共抽取了名家长进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是.(2)、将条形统计图补充完整;(3)、该学校共有2000名学生家长,估计该学校家长表示“支持”的( 类, 类的和)人数大约有多少人?20. 如图,点 在直线 上, , 与∠1互余, 是 上一点,连接 .
(1)、这次共抽取了名家长进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是.(2)、将条形统计图补充完整;(3)、该学校共有2000名学生家长,估计该学校家长表示“支持”的( 类, 类的和)人数大约有多少人?20. 如图,点 在直线 上, , 与∠1互余, 是 上一点,连接 . (1)、 是否平行于 ,请说明理由;(2)、若 平分 , ,求∠1的度数.21. 某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.
(1)、 是否平行于 ,请说明理由;(2)、若 平分 , ,求∠1的度数.21. 某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.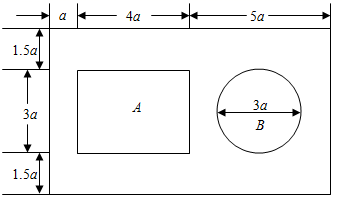 (1)、活动场所和花草的面积各是多少;(2)、整座健身馆的面积是成年人活动场所面积的多少倍.22. 甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款80000元,乙公司共捐款160000元,下面是甲、乙两公司员工的一段对话:
(1)、活动场所和花草的面积各是多少;(2)、整座健身馆的面积是成年人活动场所面积的多少倍.22. 甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款80000元,乙公司共捐款160000元,下面是甲、乙两公司员工的一段对话: (1)、甲、乙两公司各有多少人?(2)、现甲、乙两公司共同使用这笔捐款购买 、 两种防疫物资, 种防疫物资每箱15000元, 种防疫物资每箱12000元.若购买 防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注 、 两种防疫物资均需购买,并按整箱配送).23. 若 满足 ,求 的值.
(1)、甲、乙两公司各有多少人?(2)、现甲、乙两公司共同使用这笔捐款购买 、 两种防疫物资, 种防疫物资每箱15000元, 种防疫物资每箱12000元.若购买 防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注 、 两种防疫物资均需购买,并按整箱配送).23. 若 满足 ,求 的值.解:设 , ,
则 , ,
∴ .
请仿照上面的方法求解下面问题:
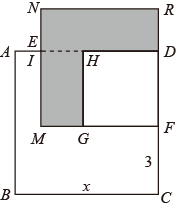 (1)、若 满足 ,求 的值;(2)、已知正方形 的边长为 , , 分别是 , 上的点,且 , ,长方形 的面积是35,分别以 , 为边作正方形 和正方形 ,求阴影部分的面积.24. 已知 ,点 在直线 , 之间,连接 , ,如图1,易得 .(1)、若 ,请在如图1中画出 的角平分线 , 的角平分线 , , 两线交于点 ,利用上述结论,求 的度数;
(1)、若 满足 ,求 的值;(2)、已知正方形 的边长为 , , 分别是 , 上的点,且 , ,长方形 的面积是35,分别以 , 为边作正方形 和正方形 ,求阴影部分的面积.24. 已知 ,点 在直线 , 之间,连接 , ,如图1,易得 .(1)、若 ,请在如图1中画出 的角平分线 , 的角平分线 , , 两线交于点 ,利用上述结论,求 的度数;

 (2)、若 平分 ,将线段 沿 平移至 .
(2)、若 平分 ,将线段 沿 平移至 .①如图2,若 , 平分 ,求 的度数;
②如图3,若 平分 ,请写出 与 的数量关系,并说明理由.