江苏省扬州市仪征市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、a³•a²=a⁶ B、a⁸÷a²=a⁴ C、（a³）²=a⁶ D、a+2a²=3a²

查看试题解析
2. 已知一个多边形的内角和是540°，则这个多边形是（）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
3. 如果a<b，下列各式中正确的是（）

A、ac²<bc² B、 $\frac{1}{a} > \frac{1}{b}$ C、 $\frac{a}{4} > \frac{b}{4}$ D、-3a>-3b

查看试题解析
4. 如图，直线AB∥CD，则下列结论正确的是（）

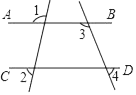A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°

查看试题解析
5. 如图，为了估计池塘两岸A、B间的距离，小明在池塘的一侧选一个点P，测得PA＝14m，PB＝10m，则AB间的距离不可能是（）

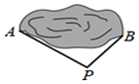A、5m B、15m C、20m D、24m

查看试题解析
6. 一个人沿北偏东60°方向从A点走到B点，再从B点沿南偏东15°方向走到C点，最后从C点向西恰好回到A点，那么∠ACB等于（）

A、45° B、75° C、90° D、105°

查看试题解析
7. 已知关于x、y的方程组 ${\begin{matrix} a x + 3 y = 10 \\ b x + 2 y = 6 \end{matrix}$ 的解是 ${\begin{matrix} x = 2 \\ y = 2 \end{matrix}$ ，则关于m、n方程组 ${\begin{matrix} a (m + n) + 3 (m - n) = 10 \\ b (m + n) + 2 (m - n) = 6 \end{matrix}$ 的解为（）

A、 ${\begin{array}{l} m = 2 \\ n = 0 \end{array}$ B、 ${\begin{array}{l} m = 2 \\ n = 2 \end{array}$ C、 ${\begin{array}{l} m = 8 \\ n = 2 \end{array}$ D、 ${\begin{array}{l} m = 1 \\ n = 1 \end{array}$

查看试题解析
8. 如图，在△ABC中，∠A＝78°，∠EBD＝∠EDB，DF平分∠EDC，则∠BDF的度数为（）

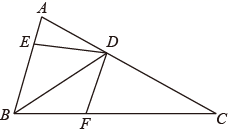A、35° B、39° C、40° D、45°

查看试题解析

二、填空题

9. 环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．如果1微米=0.000001米，那么数据0.0000025用科学记数法可以表示为．

查看试题解析
10. 已知 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是二元一次方程 $m x + 2 y = 1$ 的解，则m的值为.

查看试题解析
11. 已知a^m＝10，b^m＝2，则（ab）^m＝.

查看试题解析
12. 命题“对顶角相等”的逆命题是

查看试题解析
13. 如图，将△ABE向右平移3cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是cm.

查看试题解析
14. 如图，AD是△ABC的外角∠CAE的平分线，∠B＝40°，∠DAE＝55°，则∠ACB的度数是.

查看试题解析
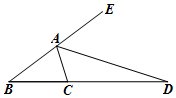15. 当三角形中一个内角是另一个内角的 $3$ 倍时，我们称此三角形为“梦想三角形”．如果一个“梦想三角形”有一个角为 $108 °$ ，那么这个“梦想三角形”的最小内角的度数为．

查看试题解析
16. 如图，大长方形由2个完全一样的大正方形、2个完全一样的小正方形和5个完全一样的小长方形拼成.若这个大长方形的周长为48cm，四个正方形的面积之和为68cm² ，则其中一个小长方形的面积是cm².

查看试题解析
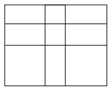17. 已知x=3是关于x的方程kx+b=0（k≠0，b＞0）的解，则关于x的不等式k（x-4）+b＞0的解集是.

查看试题解析
18. 某段高速公路全长200千米，交警部门在高速公路上距离入口3千米处设立了限速标志牌，并在以后每隔5千米处都设置一块限速标志牌；此外，交警部门还在距离入口10千米处设置了摄像头，并在以后每隔18千米处都设置一个摄像头（如图），则在此段高速公路上，离入口千米处刚好同时设置有标志牌和摄像头.

查看试题解析

三、解答题

19. 计算：

(1)、（ $\frac{1}{3}$ ）^﹣1+（﹣3）⁰﹣（﹣2）；

(2)、（﹣3a³）²+2a²•a⁴﹣a⁸÷a².

查看试题解析
20. 分解因式：

(1)、4x²﹣12xy+9y²；

(2)、4a²﹣16.

查看试题解析
21. 解方程组或不等式组：

(1)、 ${\begin{matrix} 3 x + y = 5 \\ x - 2 y = 4 \end{matrix}$ ；

(2)、 ${\begin{matrix} 5 x - 2 > 3 (x - 2) \\ \frac{1}{2} x - 5 \leq 1 - \frac{3}{2} x \end{matrix}$ .

查看试题解析
22. 先化简，再求值：（x-1）²-2（x+3）（x-3）+x（x-4），其中x=3.

查看试题解析
23. 已知关于x，y的方程组 ${\begin{matrix} 2 x + y = m + 7 \\ x + 2 y = 8 - m \end{matrix}$ （m是常数）.

(1)、若此方程组的解满足x≥0，y＞0，求m的取值范围；

(2)、在（1）的条件下，化简：|m+2|+|m﹣3|.

查看试题解析
24. 已知：如图，CD⊥AB，FG⊥AB，垂足分别为D、G，点E在AC上，且∠1＝∠2.

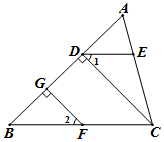(1)、求证：DE $//$ BC；

(2)、如果∠B＝46°，且∠A比∠ACB小10°，求∠DEC的度数.

查看试题解析
25. 王老师在水果店用54元买了苹果和橘子共8千克，已知苹果每千克8元，橘子每千克6元.

(1)、根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
甲： ${\begin{matrix} x + y = () \\ 8 x + 6 y = () \end{matrix}$ ；乙： ${\begin{matrix} x + y = () \\ \frac{x}{8} + \frac{y}{6} = () \end{matrix}$

根据甲、乙两名同学所列的方程组，请你分别指出未知数x、y表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：

甲：x表示， y表示；

乙：x表示， y表示.

(2)、求王老师买苹果和橘子各花了多少元钱？（写出完整的解答过程）

查看试题解析
26. 下面是某同学对多项式（x²﹣4x+2）（x²﹣4x+6）+4进行因式分解的过程.
解：设x²﹣4x＝y，

原式＝（y+2）（y+6）+4（第一步）＝y²+8y+16（第二步）＝（y+4）²（第三步）＝（x²﹣4x+4）²（第四步）

(1)、该同学第二步到第三步运用了因式分解的_______.

A、提取公因式； B、平方差公式； C、两数和的完全平方公式； D、两数差的完全平方公式.

(2)、该同学因式分解的结果是否彻底？.（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果 .

(3)、请你模仿以上方法尝试对多项式（x²+2x）（x²+2x+2）+1进行因式分解.

查看试题解析
27. 对非负数x“四舍五入”到个位的值记为〈x〉，即当n为非负整数时，若n﹣0.5≤x＜n+0.5，则〈x〉＝n.反之，当n为非负整数时，若〈x〉＝n，则n﹣0.5≤x＜n+0.5.如〈1.34〉＝1，〈4.86〉＝5.

(1)、〈π〉＝；

(2)、若〈0.5x﹣1〉＝7，则实数x的取值范围是；

(3)、若关于x的不等式组 ${\begin{matrix} \frac{2 x - 1}{3} \geq - 1 \\ x - 〈 a 〉 < 0 \end{matrix}$ 的整数解恰有4个，求a的取值范围；

(4)、满足〈x〉＝ $\frac{6}{5}$ x的所有非负数x的值为 .

查看试题解析
28. 已知：DE $//$ PQ，点A在直线DE上，点B、C都在PQ上（点B在点C的左侧），连接AB，AC，AB平分∠CAD.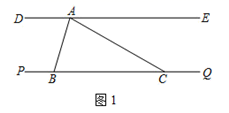

(1)、如图1，求证：∠ABC＝∠BAC；

(2)、如图2，点K为AB上一点，连接CK，若CK⊥AB，判断∠EAC与∠ACK之间的数量关系，并说明理由；

(3)、在（2）的条件下，在直线DE上取一点F，连接FK，使得∠AKF＝30°.若∠DAB＝∠AFK+∠KCB，求∠ACB的度数.（要求：在备用图中画出图形后，再计算）

查看试题解析