江苏省扬州市江都区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，计算结果为 $m^{8}$ 的是（）

A、 $m^{2} \cdot m^{4}$ B、 $m^{4} + m^{4}$ C、 $m^{16} \div m^{2}$ D、 ${(m^{2})}^{4}$

查看试题解析
2. 如图，一把长方形直尺沿直线断开并错位，点 E，D，B，F 在同一条直线上．若∠EDA=123°，则∠CBD 的度数是（　　）

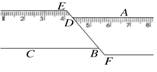A、47° B、57° C、67° D、123°

查看试题解析
3. 不等式组 ${\begin{cases} 3 x - 1 \geq 2 \\ 8 - 4 x > 0 \end{cases}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
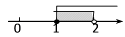4. 已知x²＋2mx＋9是完全平方式，则m的值为（）

A、±3 B、3 C、±6 D、6

查看试题解析
5. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．”诗中后两句的意思是：如果每一间客房住7人，那么有7人无房住；如果每一间客房住9人，那么就空出一间客房．设该店有客房x间、房客y人，下列方程组中正确的是（）

A、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x - 1) = y \end{matrix}$ B、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x + 1) = y \end{matrix}$ C、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x - 1) = y \end{matrix}$ D、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x + 1) = y \end{matrix}$

查看试题解析
6. 若 $x = 3$ 是关于x的不等式 $x > 2 (x - a)$ 的一个解，则a的取值范围是（）

A、 $a < \frac{3}{2}$ B、 $a > \frac{3}{2}$ C、 $a \leq \frac{3}{2}$ D、 $a \geq \frac{3}{2}$

查看试题解析
7. 如图， $A D // B C$ ， $A C$ 平分 $∠ B C D$ ， $A E$ 是 $∠ D A B$ 的平分线，若 $∠ C A E = 20 °$ ，则 $∠ D$ 与 $∠ B$ 的差是（）

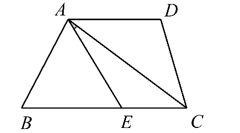A、20° B、30° C、40° D、60°

查看试题解析
8. 对有理数a，b定义运算： $a ★ b = m a + n b$ ，其中m，n是常数.如果 $3 ★ 4 = 2$ ， $5 ★ 8 > 2$ ，那么n的取值范围是（）

A、 $n > - 1$ B、 $n < - 1$ C、 $n > 2$ D、 $n < 2$

查看试题解析

二、填空题

9. 自然界中的数学不胜枚举，蜜蜂是“天才的数学家兼设计师”，蜜蜂蜂房是严格的六角柱状体，蜂房的巢壁厚0.000073米，是令人惊叹的神奇天然建筑物.数据0.000073用科学记数法表示为.

查看试题解析
10. 命题：“任意两个负数之和是负数”的逆命题是命题.（填“真”或“假”）.

查看试题解析
11. 已知 $a^{x} = 3$ ， $a^{y} = 5$ ，则 $a^{3 x - 2 y}$ 的值为.

查看试题解析
12. 一个多边形内角和与外角和共1620°，则它是边形.

查看试题解析
13. 已知 ${(a + b)}^{2} = 3$ ， ${(a - b)}^{2} = 5$ ，则 $a b =$ .

查看试题解析
14. 已知 $x^{2} + x - 1 = 0$ ，则代数式 $x (x + 3) + (x + 2) (x - 3)$ 的值为.

查看试题解析
15. 将一副直角三角板如图放置， $∠ A = 30 °$ ， $∠ F = 45 °$ .若边 $A B$ 经过点D，则 $∠ E D B =$ °.

查看试题解析
16. 在一个三角形中，如果一个内角是另一个内角的2倍，那么这个三角形称为理想三角形；如果一个内角是另一个内角的3倍，那么这个三角形称为梦想三角形.若一个三角形既是理想三角形，也是梦想三角形，写出这个三角形的三个内角的度数（只写出一组）.

查看试题解析
17. 如图， $△ A B C$ 沿 $E F$ 折叠使点A落在点 $A^{'}$ 处， $B P$ 、 $C P$ 分别是 $∠ A B D$ 、 $∠ A C D$ 平分线，若 $∠ P = 30 °$ ， $∠ A^{'} E B = 20 °$ ，则 $∠ A^{'} F C =$ °.

查看试题解析
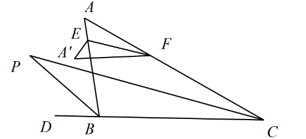18. 无论实数a取何值，关于x，y的二元一次方程 $(2 a + 1) x + (a - 1) y + 2 + a = 0$ 都有一个相同的解，则这个相同的解是.

查看试题解析

三、解答题

19. 计算：

(1)、 $- 2^{3} + {(π - 3.14)}^{0} - {(- \frac{1}{2})}^{- 1}$

(2)、 $a^{3} \cdot a^{5} + {(- a^{2})}^{4} - 3 a^{8}$

查看试题解析
20. 因式分解：

(1)、 $2 x^{3} y + 4 x^{2} y^{2} + 2 x y^{3}$

(2)、 $4 a^{2} (a - b) + (b - a)$

查看试题解析
21. 解方程组或不等式组：

(1)、 ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$

(2)、 ${\begin{array}{l} 5 x + 2 > 3 (x - 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$

查看试题解析
22. 如图， $∠ B A P + ∠ A P D = 180 °$ ， $∠ 1 = ∠ 2$ ，证明： $∠ E = ∠ F$ .完成下面推理过程.

证明：∵ $∵ ∠ B A P + ∠ A P D = 180 °$ （已知），

$∴ A B // C D$ （）.

∴_▲（两直线平行，内错角相等）.

$∵ ∠ 1 = ∠ 2$ （已知），

$∴ ∠ B A P - ∠ 1 = ∠ A P C - ∠ 2$ （），

即 $∠ E A P = ∠ F P A$ .

∴_▲_（内错角相等，两直线平行）.

$∴ ∠ E = ∠ F$ （两直线平行，内错角相等）.

查看试题解析
23. 如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点叫格点，请利用格点画图.

(1)、将 $△ A B C$ 向左平移4格，再向上平移1格，请在图中画出平移后的△A'B'C'；

(2)、 $△ A^{'} B^{'} C^{'}$ 的面积为；

(3)、利用网格在图中画出 $△ A^{'} B^{'} C^{'}$ 的中线 $B^{'} D$ ，高线 $B^{'} E$ ；

(4)、在图中能使 $S_{△ P A C} = S_{△ B A C}$ 的格点P的个数有个（点P异于B）.

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A = ∠ B C D$ ， $C D ⊥ A B$ 于点D， $B E$ 平分 $∠ A B C$ 交 $C D$ 、 $C A$ 于点F、E.

(1)、求 $∠ A C B$ 的度数；

(2)、说明： $∠ C E F = ∠ C F E$ .

(3)、若 $A C = 3 C E$ 、 $A B = 4 B D$ ， $△ A B C$ 、 $△ C E F$ 、 $△ B D F$ 的面积分别表示为 $S_{△ A B C}$ 、 $S_{△ C E F}$ 、 $S_{△ B D F}$ ，且 $S_{△ A B C} = 36$ ，则 $S_{△ C E F} - S_{△ B D F} =$ （仅填结果）.

查看试题解析
25. 已知关于a、b的方程组 ${\begin{array}{l} a - b = 1 + 3 m \\ a + b = - 7 - m \end{array}$ 中，a为负数，b为非正数.

(1)、求m的取值范围；

(2)、化简： $| m - 3 | + | m + 2 |$ ；

(3)、在m的取值范围内，当m为何整数值时，不等式 $2 m x - 3 > 2 m - 3 x$ 的解集为 $x < 1$ .

查看试题解析
26. 疫情无情，人间有爱.为扎实做好复工复课工作，教育局准备租借甲、乙两种型号的车为全市各中小学配送防疫物资.已知2辆甲型车和1辆乙型车载满物资一次可运走10吨；用1辆甲型车和2辆乙型车载满物资一次可运走11吨.

(1)、1辆甲型车和1辆乙型车都载满物资一次可分别运送多少吨？

(2)、教育局现有防疫物资37吨需要配送，计划同时租用甲、乙两种型号车共10辆，一次运完，请你帮教育局设计租车方案；

(3)、若1辆甲型车需租金100元/次，1辆乙型车需租金120元/次.请选出费用最少的租车方案，并求出最少租车费用.

查看试题解析
27. 阅读并解决问题：对于二次三项式 $x^{2} + 4 x - 12$ ，因不能直接运用完全平方公式，此时，我们可以在 $x^{2} + 4 x - 12$ 中先加上一项4，使它与 $x^{2} + 4 x$ 的和成为一个完全平方式，再减去4，整个式子的值不变，于是有： $x^{2} + 4 x - 12 = (x^{2} + 4 x + 4) - 4 - 12 = {(x + 2)}^{2} - 4^{2} = (x + 6) (x - 2)$ .像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”.

(1)、利用“配方法”分解因式： $x^{2} - 6 x + 5$ .

(2)、同时运用多项式的配方法能确定一些多项式的最大值或最小值.因为不论x取何值， ${(x + 2)}^{2} \geq 0$ ，所以当 $x = - 2$ 时，多项式 $x^{2} + 4 x - 12$ 有最小值为-16.
试确定：多项式 $- x^{2} + 2 x + 16$ 有最值（填大或小）为.

(3)、已知x是实数，试比较 $x^{2} - 4 x + 5$ 与 $- x^{2} + 4 x - 4$ 的大小，说明理由.

查看试题解析
28. 直线m与直线n相交于C，点A是直线m上一点，点B是直线n上一点， $∠ A B C$ 的平分线 $B P$ 与 $∠ D A B$ 的平分线 $A E$ 的反向延长线相交于点P.
\

(1)、如图1，若 $∠ A C B = 90 °$ ，则 $∠ P =$ ；若 $∠ A C B = α$ ，则 $∠ P =$ （结果用含 $α$ 的代数式表示）；

(2)、如图2，点F是直线n上一点，若点B在点C左侧，点F在点C右侧时，连接 $A F$ ， $∠ C A F$ 与 $∠ A F C$ 的平分线相交于点Q.
①随着点B、F的运动， $∠ A P B + ∠ A Q F$ 的值是否变化？若发生变化，请说明理由；若不发生变化，试求出其值；

②延长 $A Q$ 交直线n于点G，作 $Q H // C F$ 交 $A F$ 于点H，则 $\frac{∠ A G C - ∠ H Q F}{∠ A C B} =$ .

查看试题解析