江苏省苏州市吴中区、吴江、相城区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组值中，哪组是二元一次方程2x﹣y=5的解（）

A、 ${\begin{array}{l} x = - 2 \\ y = 6 \end{array}$ B、 ${\begin{matrix} x = 4 \\ y = 3 \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 4 \end{matrix}$ D、 ${\begin{matrix} x = 6 \\ y = 2 \end{matrix}$

查看试题解析
2. 有下列长度的三条线段，能组成三角形的是（）

A、2cm，3cm，4cm B、1cm，4cm，2cm C、1cm，2cm，3cm D、6cm，2cm，3cm

查看试题解析
3. 下列计算正确的是（）

A、 ${(2 a)}^{2} = 2 a^{2}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{2} + a^{3} = a^{5}$ D、 $a^{2} \cdot a^{3} = a^{5}$

查看试题解析
4. 如图，点E在BC的延长线上，则下列条件中，能判定 $A D / / B C$ 的是（）

A、 $∠ B = ∠ D C E$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ D + ∠ DAB = 180^{°}$

查看试题解析
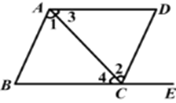5. 下列命题中，真命题的是（）

A、内错角相等 B、三角形的一个外角等于两个内角的和 C、若 $a > b > 0$ ，则 $| a | > | b |$ D、若 $2 x = - 1$ ，则 $x = - 2$

查看试题解析
6. 如图，△ABC≌△DEF，∠A=63°，∠B=70°，则∠F的度数为（）

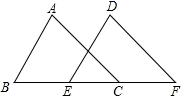A、47° B、43° C、45° D、40°

查看试题解析
7. 已知 $x = 2$ 是方程 $\frac{x + a}{3} - 3 = x - 1$ 的解，那么关于 $x$ 的不等式 $(2 - \frac{a}{2}) x < 4$ 解集是（）

A、 $x > \frac{4}{3}$ B、 $x > - \frac{4}{3}$ C、 $x < - \frac{4}{3}$ D、 $x < \frac{4}{3}$

查看试题解析
8. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．”诗中后两句的意思是：如果每一间客房住7人，那么有7人无房住；如果每一间客房住9人，那么就空出一间客房．设该店有客房x间、房客y人，下列方程组中正确的是（）

A、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x - 1) = y \end{matrix}$ B、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x + 1) = y \end{matrix}$ C、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x - 1) = y \end{matrix}$ D、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x + 1) = y \end{matrix}$

查看试题解析
9. 如图， $A B C D$ 为一长条形纸带， $A B // C D$ ，将 $A B C D$ 沿 $E F$ 折叠， $A$ 、 $D$ 两点分别与 $A^{'}$ 、 $D^{'}$ 对应，若 $∠ 1 = ∠ 2$ ，则 $∠ A E F$ 的度数为（）

A、60° B、65° C、72° D、75°

查看试题解析
10. 如图，任意画一个 $∠ B A C = 60 °$ 的 $△ A B C$ ，再分别作 $△ A B C$ 的两条角平分线 $B E$ 和 $C D$ ， $B E$ 和 $C D$ 相交于点 $P$ ，连接 $A P$ ，有以下结论：① $∠ B P C = 120 °$ ；② $S_{△ ABP} ： S_{△ ACP} = A B ： A C$ ；③ $P D = P E$ ；④ $A D = A E$ ；⑤ $B D + C E = B C$ .其中正确的结论为（）

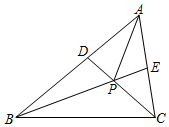A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. “蛟龙”号在海底深处的沙岩中，捕捉到一中世界上最小的神秘生物，它们的最小身长只有0.0000002米，比已知的最小细菌还要小，将0.0000002用科学记数法表示为.

查看试题解析
12. 计算 $2 x^{3} y \cdot 3 x^{2}$ 的结果是.

查看试题解析
13. 已知一个多边形的内角和是720°，则这个多边形是边形.

查看试题解析
14. 已知 $x^{m} = 6$ ， $x^{n} = 3$ ，则 $x^{2 m - n}$ 的值为．

查看试题解析
15. 已知a²﹣4b²=12，且a﹣2b=﹣3，则a+2b= ．

查看试题解析
16.
如图所示，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为

查看试题解析
17. 已知关于 $x$ 的不等式组 ${\begin{array}{l} x - a \leq 2 \\ x + 3 > 4 \end{array}$ 有且仅有3个整数解，则 $a$ 的取值范围是.

查看试题解析
18. 如图，直线 $P Q$ 经过 $R t △ A B C$ 的直角顶点 $C ， △ A B C$ 的边上有两个动点 $D ， E$ ，点 $D$ 以 $1 c m / s$ 的速度从点 $A$ 出发沿 $A C - C B$ 移动到点 $B$ ，点 $E$ 以 $3 c m / s$ 的速度从点 $B$ 出发，沿 $B C - C A$ 移动到点 $A$ ，两动点中有一个点到达终点后另一个点继续移动到终点过点 $D ， E$ 分别作 $D M ⊥ P Q ，$ $E N ⊥ P Q$ ，垂足分别为点 $M ， N$ .若 $A C = 6 c m ， B C = 8 c m$ ，设运动时间为 $t$ ，则当 $t =$ $s$ 时，以点 $D ， M ， C$ 为顶点的三角形与以点 $E ， N ， C$ 为顶点的三角形全等.

查看试题解析

三、解答题

19. 计算：

(1)、 $2^{2} - {(n - 1)}^{0} + 3^{- 1} \times (- 6)$ ；

(2)、 ${(- 2 x^{2})}^{2} + x^{3} \cdot x - x^{5} \div x$ .

查看试题解析
20. 因式分解：

(1)、 $8 - 2 a^{2}$ ；

(2)、 $(x - 1) (x - 3) + 1$ .

查看试题解析
21. 先化简，再求值： ${(x - y)}^{2} - (2 x + y) (2 x - y) + 3 x (x + y)$ ，其中 $| x + 3 | + {(y - 2)}^{2} = 0.$

查看试题解析
22.

(1)、解方程组： ${\begin{matrix} x - y = - 1 \\ 2 x + 3 y = 8 \end{matrix}$

(2)、解不等式： $\frac{2 x + 1}{4} \leq \frac{x - 1}{3}$ ，并把解集在数轴上表示出来，同时写出它的最大整数解.

查看试题解析
23. 如图，方格纸中每个小正方形的边长都为1，在方格纸内将 $△ A B C$ 经过平移后得到 $△ A^{'} B^{'} C^{'}$ ，图中标出了点 $B$ 的对应点 $B^{'}$ .根据下列条件，利用网格点和三角尺画图，并完成以下问题：

(1)、补全 $△ A^{'} B^{'} C^{'}$ ；

(2)、请在 $A C$ 边上找一点 $D$ ，使得线段 $B D$ 平分 $△ A B C$ 的面积，在图上作出线段 $B D$ ；

(3)、利用格点在图中画出 $A C$ 边上的高线 $B E$ .

(4)、点 $M$ 为方格纸上的格点（异于点 $D$ ），若 $△ M B C$ 和 $△ D C B$ 全等，则图中这样的格点 $M$ 共有个.

查看试题解析
24. 如图， $△ A B C$ 中， $D$ 为 $B C$ 上一点， $∠ C = ∠ B A D$ ， $△ A B C$ 的角平分线 $B E$ 交 $A D$ 于点 $F$ .

(1)、求证： $∠ A E F = ∠ A F E$ ；

(2)、 $G$ 为 $B C$ 上一点，当 $F E$ 平分 $∠ A F G$ 且 $∠ C = 30 °$ 时，求 $∠ C G F$ 的度数.

查看试题解析

25. 为庆祝建党100周年，学校党支部号召广大党员积极开展“学知识、获积分、赢奖品!”活动，该校准备到苏宁电器超市采购奖品，发现该超市销售

A

、

B

两种型号的电风扇，

A

型号每台进价为190元、

B

型号每台进价为160元，下表是近两周的销售情况：

销售时段	销售数量		销售额
销售时段	$A$ 种型号	$B$ 种型号	销售额
第一周	3台	3台	1320元
第二周	2台	6台	1680元

（进价、售价均保持不变，利润=销售收入-进货成本）

(1)、求

A

、

B

两种型号的电风扇的销售单价：

(2)、若超市准备再采购40台这两种型号的电风扇，且

A

型号电风扇采购数量不超过

B

型号数量的2倍，当这40台电风扇全部出售给学校且利润不低于1850元，求超市共有哪些采购方案?

查看试题解析

26. 对于未知数为 $x$ ， $y$ 的二元一次方程组，如果方程组的解 $x$ ， $y$ 满足 $| x - y | = 1$ ，我们就说方程组的解 $x$ 与 $y$ 具有“邻好关系”.

(1)、方程组 ${\begin{matrix} x + 2 y = 7 \\ x = y + 1 \end{matrix}$ 的解 $x$ 与 $y$ 是否具有“邻好关系”?说明你的理由：

(2)、若方程组 ${\begin{matrix} 4 x - y = 6 \\ 2 x + y = 4 m \end{matrix}$ 的解 $x$ 与 $y$ 具有“邻好关系”，求 $m$ 的值：

(3)、未知数为 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + a y = 7 \\ 2 y - x = 5 \end{array}$ ，其中 $a$ 与 $x$ 、 $y$ 都是正整数，该方程组的解 $x$ 与 $y$ 是否具有“邻好关系”?如果具有，请求出 $a$ 的值及方程组的解：如果不具有，请说明理由.

查看试题解析
27. 如图1， $△ A B C$ 中， $∠ A B C = ∠ A C B$ .点 $D$ 、 $E$ 、 $F$ 分别是 $A B$ 、 $B C$ 、 $A C$ 边上的点， $B E = C F$ .

(1)、若 $∠ D E F = ∠ A B C$ ，求证： $D E = E F$ ；

(2)、若 $∠ A + 2 ∠ D E F = 180 °$ ， $B C = 9$ ， $E C = 2 B E$ ，求 $B D$ 的长：

(3)、把（1）中的条件和结论反过来，即：若 $D E = E F$ ，则 $∠ D E F = ∠ A B C$ ；这个命题是否成立?若成立，请证明：若不成立，请说明理由.

查看试题解析
28. 阅读：若 $x$ 满足 $(60 - x) (x - 40) = 30$ ，求 ${(60 - x)}^{2} + {(x - 40)}^{2}$ 的值，
解：设 $(60 - x) = a$ ， $(x - 40) = b$ ，则 $(60 - x) (x - 40) = a b =$ ______， $a + b = (60 - x) + (x - 40) =$ ______，所以 ${(60 - x)}^{2} + {(x - 40)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b =$ ______.

请仿照上例解决下面的问题：

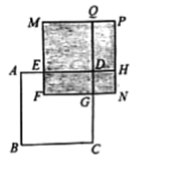(1)、补全题目中横线处：

(2)、已知 $(30 - x) (x - 20) = - 10$ ，求 ${(30 - x)}^{2} + {(x - 20)}^{2}$ 的值；

(3)、若 $x$ 满足 ${(2023 - x)}^{2} + {(2022 - x)}^{2} = 2021$ ，求 $(2023 - x) (x - 2022)$ 的值；

(4)、如图，正方形 $A B C D$ 的边长为 $x$ ， $A E = 10$ ， $C G = 25$ ，长方形 $E F G D$ 的面积是400，四边形 $N G D H$ 和 $M E D Q$ 都是正方形， $P Q D H$ 是长方形，求图中阴影部分的面积（结果必须是一个具体数值）.

查看试题解析