江苏省南京市江宁区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-07-30 类型:期末考试
一、单选题
-
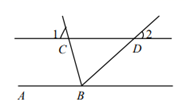
1. 代数式a3•a2化简后的结果是( )A、a B、a5 C、a6 D、a92. 氢原子的半径约为0.00000000005m,用科学记数法表示0.00000000005是( )A、5×10-9 B、0.5×10-10 C、5×10-11 D、5×10-123. 若a>b,则下列不等式不成立的是( )A、a+3>b+3 B、3a>3b C、 D、-3a>-3b4. 如图,AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的度数是( )
 A、65° B、60° C、55° D、50°5. 已知M=3x2-x+3,N=2x2+3x-1,则M、N的大小关系是( )A、M≥N B、M>N C、M≤N D、M<N6. 如图,△ABC的中线AD、BE相交于点F.若△ABF的面积是4,则四边形DCEF的面积是( )
A、65° B、60° C、55° D、50°5. 已知M=3x2-x+3,N=2x2+3x-1,则M、N的大小关系是( )A、M≥N B、M>N C、M≤N D、M<N6. 如图,△ABC的中线AD、BE相交于点F.若△ABF的面积是4,则四边形DCEF的面积是( )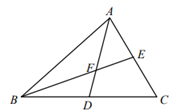 A、3.5 B、4 C、4.5 D、5
A、3.5 B、4 C、4.5 D、5二、填空题
-
7. 计算:(-2)0=;2-1=.8. “两直线平行,内错角相等”的逆命题是 .9. 分解因式: =.
10. 把方程2x+y=3改写成用含x的式子表示y的形式,得y= .11. 已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为.
12. 如图,直线a、b被直线c所截,∠1=50°.当∠2=°时,a∥b.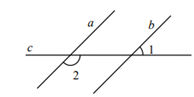 13. 关于x,y的方程组 的解满足x-y=6,则m=.14. 如图,点D在AB上,点E在AC上,BE、CD相交于点O,∠A=40°,∠C=30°,∠BOD=100°.则∠B=°.
13. 关于x,y的方程组 的解满足x-y=6,则m=.14. 如图,点D在AB上,点E在AC上,BE、CD相交于点O,∠A=40°,∠C=30°,∠BOD=100°.则∠B=°.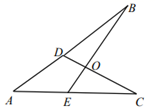 15. 如图,∠A+∠B+∠C+∠D+∠E+∠F=°.
15. 如图,∠A+∠B+∠C+∠D+∠E+∠F=°.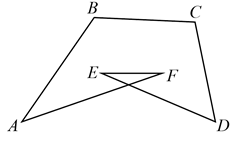 16. 若关于x的一元一次不等式组 仅有2个整数解,则m的取值范围是.
16. 若关于x的一元一次不等式组 仅有2个整数解,则m的取值范围是.三、解答题
-
17. 计算(1)、(2a2)3÷(a2)2;(2)、(a+b)(a-3b).18. 分解因式(1)、2a(x-y)+b(y-x);(2)、4a2-16a+16.19. 先化简,再求值:(a+2b)(a-2b)+(a-2b)2 , 其中,a= ,b=1.20. 解方程组21. 解不等式组 请结合题意,完成本题的解答.(1)、解不等式①,得 .(2)、解不等式③,得.(3)、把不等式①、②和③的解集在数轴上表示出来.
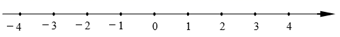 (4)、从图中可以找出三个不等式解集的公共部分,得不等式组的解集.22. 画图并填空:
(4)、从图中可以找出三个不等式解集的公共部分,得不等式组的解集.22. 画图并填空:如图,方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移,使点C移到点C'的位置.
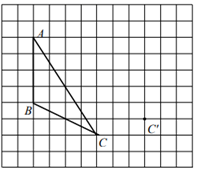 (1)、请画出△A'B'C';(2)、连接AA'、BB',则这两条线段的关系是;(3)、在方格纸中,画出△ABC的中线BD和高CE;(4)、线段AB在平移过程中扫过区域的面积为.23. 如图,GF∥CD,∠1=∠2.求证:∠CED+∠ACB=180°.
(1)、请画出△A'B'C';(2)、连接AA'、BB',则这两条线段的关系是;(3)、在方格纸中,画出△ABC的中线BD和高CE;(4)、线段AB在平移过程中扫过区域的面积为.23. 如图,GF∥CD,∠1=∠2.求证:∠CED+∠ACB=180°.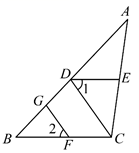 24. 为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买7个足球和5个篮球的费用相同;购买40个足球和20个篮球共需3400元.(1)、求每个足球和篮球各多少元?(2)、如果学校计划购买足球和篮球共80个,总费用不超过4800元,那么最多能买多少个篮球?25. 如图,∠1,∠2,∠3,∠4是四边形ABCD的四个外角.
24. 为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买7个足球和5个篮球的费用相同;购买40个足球和20个篮球共需3400元.(1)、求每个足球和篮球各多少元?(2)、如果学校计划购买足球和篮球共80个,总费用不超过4800元,那么最多能买多少个篮球?25. 如图,∠1,∠2,∠3,∠4是四边形ABCD的四个外角.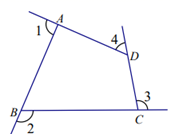
用两种方法证明∠1+∠2+∠3+∠4=360°.
26. 两条直线相交所形成的较小的角称为这两条直线的夹角.如:直线m、n相交,其夹角为60°,特别的,如果m⊥n,那么其夹角为90°. (1)、如图①,MN∥PQ,含45°的直角三角形ABC的三边和两条平行线有4个交点D、E、F、G,若AB和PQ的夹角为65°,求∠CFQ与∠CEN的度数.
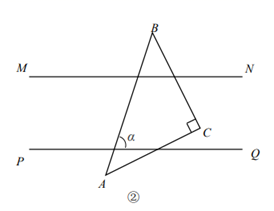
(1)、如图①,MN∥PQ,含45°的直角三角形ABC的三边和两条平行线有4个交点D、E、F、G,若AB和PQ的夹角为65°,求∠CFQ与∠CEN的度数. (2)、如图②,MN∥PQ,将一块含45°的直角三角板ABC任意摆放在两条平行线上(三角板足够大),使三角板的三边和两条平行线始终有4个交点.设斜边AB所在直线与MN(或PQ)的夹角为α(0°<α≤90°),直接写出4个交点处的夹角之和.(结果可以用含α的代数式表示)
(2)、如图②,MN∥PQ,将一块含45°的直角三角板ABC任意摆放在两条平行线上(三角板足够大),使三角板的三边和两条平行线始终有4个交点.设斜边AB所在直线与MN(或PQ)的夹角为α(0°<α≤90°),直接写出4个交点处的夹角之和.(结果可以用含α的代数式表示)