湖南省娄底市娄星区2020-2021学年七年级下学期数学期末考试试卷
试卷更新日期:2021-07-30 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、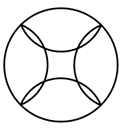 D、
D、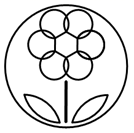 2. 方程组 的解是( )A、 B、 C、 D、3. 多项式 中,各项的公因式是( )A、 B、 C、 D、4. 下列各式中,计算正确的是( )A、 B、 C、 D、5. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八盈三;人出七,不足四.问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱.问人数、物价各是多少?设合伙人数为 人,物价为 钱,则下列方程组正确的是( )A、 B、 C、 D、6. 下列因式分解正确的是( )A、 B、 C、 D、7. 如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( )
2. 方程组 的解是( )A、 B、 C、 D、3. 多项式 中,各项的公因式是( )A、 B、 C、 D、4. 下列各式中,计算正确的是( )A、 B、 C、 D、5. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八盈三;人出七,不足四.问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又会差4钱.问人数、物价各是多少?设合伙人数为 人,物价为 钱,则下列方程组正确的是( )A、 B、 C、 D、6. 下列因式分解正确的是( )A、 B、 C、 D、7. 如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( ) A、① B、② C、③ D、④8. 如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是( )
A、① B、② C、③ D、④8. 如图,已知AC⊥BC,CD⊥AB,垂足分别是C,D,其中AC=6,BC=8,AB=10,CD=4.8,那么点B到AC的距离是( )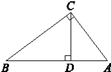 A、6 B、8 C、10 D、4.89. 在今年的体育考试中,某校甲、乙、丙三个班级的平均分相等,方差分别为: , , ,则这三个班学生的体育考试成绩最整齐的是( )A、甲班 B、乙班 C、丙班 D、不能确定10. 若 是一个完全平方式,则常数k的值为A、6 B、 C、 D、无法确定11. 给出下列说法:
A、6 B、8 C、10 D、4.89. 在今年的体育考试中,某校甲、乙、丙三个班级的平均分相等,方差分别为: , , ,则这三个班学生的体育考试成绩最整齐的是( )A、甲班 B、乙班 C、丙班 D、不能确定10. 若 是一个完全平方式,则常数k的值为A、6 B、 C、 D、无法确定11. 给出下列说法:( 1 )两条直线被第三条直线所截,同位角相等;
( 2 )不相等的两个角不是同位角;
( 3 )平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
( 4 )从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离;
其中正确的说法有( )
A、0个 B、1个 C、2个 D、3个12. 甲、乙两农户各有两块地,如图所示,今年,这两个农户决定共同投资搞饲养业.为此,他们准备将这4块土地换成一块地,那块地的宽为(a+b)米,为了使所换土地的面积与原来4块地的总面积相等,交换之后的土地的长应该是( )米. A、a+b B、b+c C、a+c D、a+b+c
A、a+b B、b+c C、a+c D、a+b+c二、填空题
-
13. 因式分解: =14. 若 ,则 .15. 已知 a+b=5,ab=1 , 则 .16. 一组数据:6、3、4、x、7,它们的平均数是5,则这组数据的中位数是。17. 如图AO⊥BO, , 平分 ,则 的度数为 .
 18. 如图,直线a∥b , 点A , B位于直线a上,点C , D位于直线b上,且AB:CD=1:2,如果△ABC的面积为10,那么△BCD的面积为 .
18. 如图,直线a∥b , 点A , B位于直线a上,点C , D位于直线b上,且AB:CD=1:2,如果△ABC的面积为10,那么△BCD的面积为 .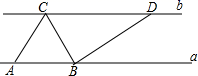
三、解答题
-
19. 解下列方程组:(1)、 ;(2)、 .20. 分解因式(1)、 ;(2)、 .21. 求代数式的值(1)、先化简,再求值: ,其中 .(2)、已知 可以分解为一次因式 和 ,求 的值.22. 如图在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.

(1)请作出△OAB关于直线CD对称的△O1A1B1;
(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.23. 如图, 于点F, 于点E,若 ,则 .完成下面的说理过程.
解: ,理由如下:
因为 , (已知),
所以 .
所以_▲_//_▲_ ( ).
因此 ( ).
又因为 (已知),
且 ( ) (平角的意义),
所以 ( )
因此 _▲_(等量代换).
所以 ( ).
24. 为了迎接建党100周年,某班组织了“我和我的祖国”演讲比赛,甲、乙两队各有五人参加比赛,得分如下(10分制)甲队
8
10
8
6
8
乙队
7
9
5
10
9
(1)、甲队成绩的众数是分,乙队成绩的中位数是分.(2)、计算乙队成绩的平均数和方差.(3)、已知甲队成绩的方差是1.6,则成绩比较稳定的是哪个队,并说明理由.25. 在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.求每次购买的酒精和消毒液分别是多少瓶?26. (问题情境):如图 // , , ,求 的度数.小明的思路是:过 作 // ,通过平行线性质来求 .
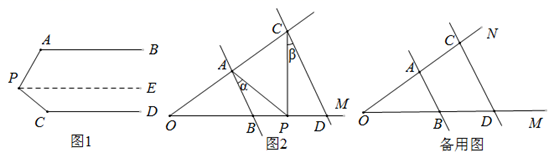 (1)、按小明的思路,求 的度数;(2)、(问题迁移):如图2,AB//CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;(3)、(问题应用):在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
(1)、按小明的思路,求 的度数;(2)、(问题迁移):如图2,AB//CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;(3)、(问题应用):在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.