福建省龙岩市五县市区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-30 类型：期末考试

进入出卷网下载

一、单选题

1. 点P(2，－3)所在的象限是( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列调查中，适合用普查的是（）

A、新冠疫情期间检测地铁乘客的体温 B、调查全中国中学生的近视率 C、调查某品牌电视机的使用寿命 D、调查长江中现有鱼的种类

查看试题解析
3. 若 $a > b$ ，则下列不等式中一定成立的是（）

A、 $a + c > b + c$ B、 $c - a > c - b$ C、 $a c^{2} > b c^{2}$ D、 $\frac{a}{c} > \frac{b}{c}$

查看试题解析
4. 已知点P（8−2m，m+1）在 $x$ 轴上，则点 $P$ 的坐标为（）

A、（0，7） B、（0，5） C、（10，0） D、（6，0）

查看试题解析
5. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
6. 如图，直线 $A B / / C D$ ，直线 $E F$ 分别交 $A B 、 C D$ 于 $E 、 F$ 两点， $E G$ 平分 $∠ A E F$ ，若 $∠ 1 = 35 °$ ，则 $∠ 2$ 的等于（）

A、 $35 °$ B、 $55 °$ C、 $68 °$ D、 $70 °$

查看试题解析
7. 定义：对于实数 $a$ ，符号 $[a]$ 表示不大于 $a$ 的最大整数.例如：[3.2]=3，[2]=2，[-2.3]=-3.如果 $[\frac{x - 1}{2}] = 2$ ，则 $x$ 的取值范围是（）

A、 $5 \leq x \leq 7$ B、 $5 < x \leq 7$ C、 $5 < x < 7$ D、 $5 \leq x < 7$

查看试题解析
8. 若不等式组 ${\begin{array}{l} x \geq a + 1 \\ x < 3 \end{array}$ 恰有3个整数解，则 $a$ 的取值范围是（）

A、 $a \leq 1$ B、 $- 2 < a \leq - 1$ C、 $a < - 1$ D、 $- 2 \leq a < - 1$

查看试题解析
9. 如图，已知 $A F / / C D ， ∠ B A F = ∠ E A F$ ，则 $\frac{∠ A E C + ∠ A B F}{∠ E C D}$ 的值（）

A、不确定 B、等于1 C、等于2 D、大于2

查看试题解析

二、填空题

10. 为了解某县近40000名八年级学生的体重情况，随机抽取其中800名学生的体重进行调查，则此次调查的样本容量是.

查看试题解析
11. 已知 $△ A B C$ 的边 $A B = 4 cm$ ，将 $△ A B C$ 沿着 $A B$ 方向平移得到 $△ A^{'} B^{'} C^{'}$ ，已知 $A' B = lcm$ ，则 $C C' =$ $cm$ .

查看试题解析
12. 方程组 ${\begin{array}{l} 4 x + 5 y = 2 \\ 2 x - 3 y = - 10 \end{array}$ 的解为.

查看试题解析
13. 若关于 $x ， y$ 的方程组 ${\begin{array}{l} x - y = 3 \\ x + a y = 0 \end{array}$ 的解也是方程 $x + y = 1$ 的解，则 $a$ 的值为.

查看试题解析
14. 设 $a$ 是 $2 + \sqrt{6}$ 的整数部分， $b$ 是 $2 - \sqrt{6}$ 的小数部分，则 $a + b =$ .

查看试题解析
15. 如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“ $\to$ ”方向排行，如（0，1），（0，2），（1，2），（1，3），（0，3），（-1，3），......根据这个规律探索可得，第40个点的坐标为.

查看试题解析

三、解答题

16. 计算： $\sqrt[3]{- 8} + \sqrt{36} - \sqrt{3} + | 1 - \sqrt{3} |$ .

查看试题解析
17. 解方程组： ${\begin{array}{l} \frac{x}{2} + \frac{y}{3} = 2 \\ 4 (x - y - 1) = 3 (1 - y) - 2 \end{array}$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} \frac{x + 3}{3} - 3 \geq x - 1 \\ 1 - 2 (x - 1) < 8 - x \end{array}$ ，并求出该不等式组的所有整数解的和.

查看试题解析
19. 完成下面的证明，如图， $A D / / B E$ ， $∠ 1 = ∠ 2$ ，求证： $∠ A = ∠ E$ .

证明：∵ $A D / / B E$ （已知），

∴ $∠ A =$ _▲_（   ）

∵ $∠ 1 = ∠ 2$ （已知），

∴ $D E / /$ _▲（   ）.

∴ $∠ E =$ _▲_（   ）.

∴ $∠ A = ∠ E$ （等量代换）.

查看试题解析
20. 如图直角三角形ABC中， $∠ B = 30^{\circ}$ ， $C E$ 平分 $∠ A C B$ ， $∠ E A D = 2 ∠ C A F$ ，求证： $C E / / F D$ .

查看试题解析
21. 为加强中学生身体素质，某中学积极开展体育活动，现抽取若干名学生进行最喜爱的运动项目的问卷调查，整理、绘制成如下不完整的统计图（图①、图②），请根据统计图提供的信息，回答下列问题：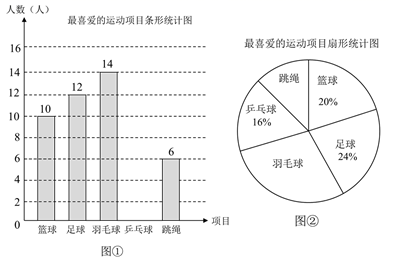

(1)、求抽取的学生人数.

(2)、补全条形统计图.

(3)、若该校共有学生1500名，请你估计喜欢羽毛球的学生人数.

查看试题解析
22. 如图，已知 $A B$ ∥ $C D$ ， $∠ A = ∠ C$ ，线段 $A D$ 上从左到右依次有两点 $E ， F$ （不与 $A ， D$ 重合）.

(1)、求证： $A D$ ∥ $B C$ ；

(2)、比较 $∠ 1$ 、 $∠ 2$ 、 $∠ 3$ 的大小，并说明理由；

(3)、若 $∠ A = ∠ E B F = \frac{1}{2} ∠ A B E ， ∠ C B D = 3 ∠ F B D$ ，求 $∠ E B D$ 的度数.

查看试题解析

23. 某县2021以来受持续干旱影响，河道来水偏少，已严重影响生产和生活用水，自来水厂推行阶梯水价，引导人们节约用水，调整后的用水价格如下：

每月用水量（吨）	单价（元/吨）
不超过20的部分	1.5
超过20不超过30的部分	2
超过30的部分	3

(1)、小明家5月份的用水量为23吨，小明家5月份的水费是多少？

(2)、小明家1月份水费的均价为1.75元/吨，求小明家1月份的用水量？

(3)、小明家3、4两个月的总用水量为56吨（4月份用水较少），3、4两个月的水费合计93元，请问小明家3、4月份的用水量分别是多少？

查看试题解析

24. 如图，在平面直角坐标系中，O为坐标原点，点 $A (a ， b) 、 B (c ， 0)$ ，其中 $a ， b ， c$ 满足 $| a - 2 | + {(b - 3)}^{2} + \sqrt{c + 4} = 0$ ，D为直线AB与 $y$ 轴的交点，C为线段AB上一点，其纵坐标为 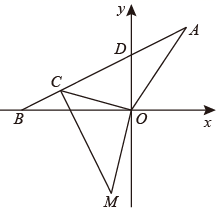$t$ .

(1)、求 $a ， b ， c$ 的值；

(2)、当 $t$ 为何值时， $△ BOC$ 和 $△ AOD$ 面积的相等；

(3)、若点C坐标为（-2，1），点M（m，-3）在第三象限内，满足 $S_{△ MOC} \geq 5$ ，求m的取值范围.
（注： $S_{△ MOC}$ 表示 $△ MOC$ 的面积）

查看试题解析