云南省文山州2021年中考数学模拟试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 2021年4月11日,国家卫健委通报:截至4月10日24时,全国累计报告接种新冠疫苗16447.1万剂次,将16447.1用科学记数法表示为( )A、 B、 C、 D、2. 根据图中三视图可知该几何体是( )
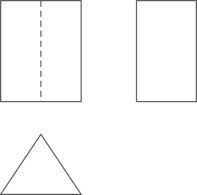 A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在 中,若 ,则 ( )
A、三棱锥 B、三棱柱 C、四棱锥 D、四棱柱3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在 中,若 ,则 ( ) A、4 B、8 C、9 D、125. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨6. 某超市正在热销一种商品,其标价为每件12元,打8折销售后每件可获利2元,该商品每件的进价为( )A、7.6元 B、7.7元 C、7.8元 D、7.9元7. 在平面直角坐标系中,一次函数 的图象是( )A、
A、4 B、8 C、9 D、125. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨6. 某超市正在热销一种商品,其标价为每件12元,打8折销售后每件可获利2元,该商品每件的进价为( )A、7.6元 B、7.7元 C、7.8元 D、7.9元7. 在平面直角坐标系中,一次函数 的图象是( )A、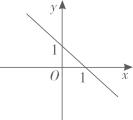 B、
B、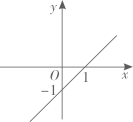 C、
C、 D、
D、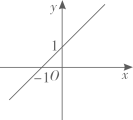 8. 若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为( )A、 B、 C、 或 D、 或
8. 若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为( )A、 B、 C、 或 D、 或二、填空题
-
9. 因式分解: =.10. 正五边形的外角和等于 ◦.
11. 若代数式 有意义,则实数x的取值范围是 .12. 已知点(2,﹣2)在反比例函数y= 的图象上,则这个反比例函数的表达式是 .13. 如图,直线a、b被直线c所截, , ,那么 . 14. 如图,在平面直角坐标系中,点 在x轴正半轴上,点 在直线 上,若 的坐标为 ,且 均为等边三角形,则线段 的长度为 .
14. 如图,在平面直角坐标系中,点 在x轴正半轴上,点 在直线 上,若 的坐标为 ,且 均为等边三角形,则线段 的长度为 .
三、解答题
-
15. 计算: .16. 如图, 、 .求证: .
 17. 某农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如图的统计图1和图2.请根据相关信息,解答下列问题:
17. 某农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如图的统计图1和图2.请根据相关信息,解答下列问题: (1)、求本次抽取的麦苗株数和图1中m的值,并补全条形统计图.(2)、求这组数据的平均数、众数和中位数.18. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
(1)、求本次抽取的麦苗株数和图1中m的值,并补全条形统计图.(2)、求这组数据的平均数、众数和中位数.18. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.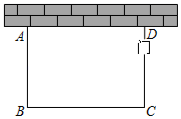 19. 有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
19. 有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.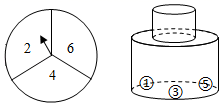 (1)、请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;(2)、若得到的两数字之和是3的倍数,则小杰赢;若得到的两数字之和是7的倍数,则小玉赢,此游戏公平吗?为什么?20. 如图,已知AB是 的直径,直线BC与 相切于点B,过点A作AD//OC交 于点D,连接CD.
(1)、请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;(2)、若得到的两数字之和是3的倍数,则小杰赢;若得到的两数字之和是7的倍数,则小玉赢,此游戏公平吗?为什么?20. 如图,已知AB是 的直径,直线BC与 相切于点B,过点A作AD//OC交 于点D,连接CD.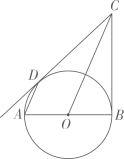 (1)、求证:CD是 的切线.(2)、若 ,直径 ,求线段BC的长.21. 如图,在矩形 中, 为对角线 的中点,过点 作直线分别与矩形的边 , 交于 , 两点,连接 , .
(1)、求证:CD是 的切线.(2)、若 ,直径 ,求线段BC的长.21. 如图,在矩形 中, 为对角线 的中点,过点 作直线分别与矩形的边 , 交于 , 两点,连接 , .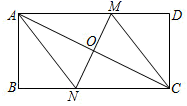 (1)、求证:四边形 为平行四边形;(2)、若 , ,且 ,求 的长22. 某县进行创建卫生城市申报工作,制作洗手台的盛水容器如图1所示.科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为H(单位: ),如果在离水面竖直距离为h(单位: )的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位: )与h的关系式为 .应用思考:现用高度为 的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离 处开一个小孔.
(1)、求证:四边形 为平行四边形;(2)、若 , ,且 ,求 的长22. 某县进行创建卫生城市申报工作,制作洗手台的盛水容器如图1所示.科学原理:如图2,始终盛满水的圆柱体水桶水面离地面的高度为H(单位: ),如果在离水面竖直距离为h(单位: )的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位: )与h的关系式为 .应用思考:现用高度为 的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离 处开一个小孔.
 (1)、写出 与h的关系式.(2)、求当h为何值时,射程s有最大值,最大射程是多少?23. 如图, 是等边三角形, ,动点P从点A出发,以 的速度沿 向点B匀速运动,过点P作 ,交折线 于点Q,以 为边作等边三角形 ,使点A,D在 异侧.设点P的运动时间为 , 与 重叠部分图形的面积为 .
(1)、写出 与h的关系式.(2)、求当h为何值时,射程s有最大值,最大射程是多少?23. 如图, 是等边三角形, ,动点P从点A出发,以 的速度沿 向点B匀速运动,过点P作 ,交折线 于点Q,以 为边作等边三角形 ,使点A,D在 异侧.设点P的运动时间为 , 与 重叠部分图形的面积为 .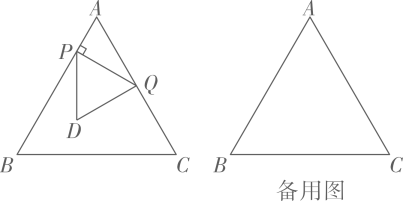 (1)、 的长为 (用含 的代数式表示).(2)、当点D落在边 上时,求x的值.(3)、求y关于x的函数解析式,并写出自变量x的取值范围.
(1)、 的长为 (用含 的代数式表示).(2)、当点D落在边 上时,求x的值.(3)、求y关于x的函数解析式,并写出自变量x的取值范围.