上海市浦东新区第四教育署2021年中考数学5月试卷

试卷更新日期：2021-07-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列正整数中，属于素数的是（　　）

A、2 B、4 C、6 D、8

查看试题解析
2. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{9}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{18}$

查看试题解析
3. 若直线y=kx+b经过一、二、四象限，则直线y=bx+k不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 某班在统计全班33人的体重时，算出中位数与平均数都是54千克，但后来发现在计算时，将其中一名学生的体重50千克错写成了5千克，经重新计算后，正确的中位数为a千克，正确的平均数为b千克，那么（　　）

A、a＜b B、a＝b C、a＞b D、无法判断

查看试题解析
5. 正六边形的半径与边心距之比为（）

A、1： $\sqrt{3}$ B、 $\sqrt{3}$ ：1 C、 $\sqrt{3}$ ：2 D、2： $\sqrt{3}$

查看试题解析
6. 下列命题中正确的个数是（）
① 过三点可以确定一个圆；② 直角三角形的两条直角边长分别是5和12，那么它的外接圆半径为6.5； ③ 如果两个半径为2厘米和3厘米的圆相切，那么圆心距为5厘米；④ 三角形的重心到三角形三边的距离相等．

A、1个； B、2个； C、3个； D、4个．

查看试题解析

二、填空题

7. 计算：a•（3a）²＝．

查看试题解析
8. 化简： $\frac{1}{a} - \frac{1}{3 a} =$ ．

查看试题解析
9. 已知关于x的方程x²-3x+m=0（m为常数）有两个相等的实数根，那么m =

查看试题解析
10. 如果将抛物线y＝2x²向左平移3个单位，那么所得新抛物线的表达式为．

查看试题解析
11. 不透明的袋中装有8个小球，这些小球除了有红白两种颜色外其它都一样，其中2个小球为红色，6个小球为白色，随机地从袋中摸取一个小球是红球的概率为．

查看试题解析

12. 秋季新学期开学时，某中学对六年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了不完整的图表（如表所示），图表中c= ．

分数段	频数	频率
60≤x＜70	6	a
70≤x＜80	20	0.4
80≤x＜90	15	b
90≤x≤100	c	0.18

查看试题解析

13. 已知反比例函数y＝ $\frac{k}{x}$ 的图象经过点（2，﹣1），则k＝．

查看试题解析
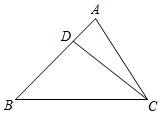
14. 如图，在△ABC中，点D在边AB上，AB＝4AD，设 $\vec{AB} = \vec{a}$ ， $\vec{AC} = \vec{b}$ ，那么向量 $\vec{DC}$ 用向量 $\vec{a}$ 、 $\vec{b}$ 表示为．

查看试题解析
15. 已知点C在线段AB上，且0＜AC＜ $\frac{1}{2}$ AB．如果⊙C经过点A，那么点B与⊙C的位置关系是．

查看试题解析
16. 如图，点M、N分别在∠AOB的边OA、OB上，将∠AOB沿直线MN翻折，设点O落在点P处，如果当OM=4，ON=3时，点O、P的距离为4，那么折痕MN的长为．

查看试题解析
17. 如果一个四边形有且只有三个顶点在圆上，那么称这个四边形是该圆的“联络四边形”，已知圆的半径长为 $5$ ，这个圆的一个联络四边形是边长为 $2 \sqrt{5}$ 的菱形，那么这个菱形不在圆上的顶点与圆心的距离是．

查看试题解析
18. 如图，点M的坐标为（3，2），点P从原点O出发，以每秒1个单位的速度沿y轴向上移动，同时过点P的直线l也随之上下平移，且直线l与直线y＝﹣x平行，如果点M关于直线l的对称点落在坐标轴上，如果点P的移动时间为t秒，那么t的值可以是．

查看试题解析

三、解答题

19. 计算：（ $\sqrt{2020}$ ﹣1）⁰＋|1﹣ $\sqrt{3}$ |＋（ $\frac{1}{3}$ ）^﹣1＋ $8^{\frac{1}{3}}$ ．

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 (x - 2) \leq 8 - (x + 6) \\ \frac{x + 1}{2} < \frac{2 x - 1}{3} + 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
21. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4，点D在边BC上，且BD＝3CD，DE⊥AB，垂足为点E，联结CE．

(1)、求线段AE的长；

(2)、求∠ACE的余切值．

查看试题解析
22. 疫情期间，甲厂欲购买某种无纺布生产口罩，A、B两家无纺布公司各自给出了该种无纺布的销售方案.
A公司方案：无纺布的价格y（万元）与其重量x（吨）是如图所示的函数关系；

B公司方案：无纺布不超过30吨时，每吨收费2万元；超过30吨时，超过的部分每吨收费1.9万元.

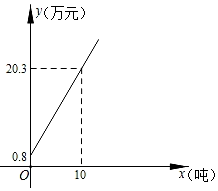(1)、求如图所示的y与x的函数解析式；（不要求写出定义域）

(2)、如果甲厂所需购买的无纺布是40吨，试通过计算说明选择哪家公司费用较少.

查看试题解析
23. 如图，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于点E，F是AB的中点，联结AE、EF，且AE⊥BE．

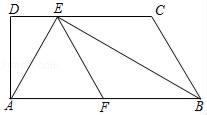
求证：

(1)、四边形BCEF是菱形；

(2)、BE•AE=2AD•BC．

查看试题解析
24. 在平面直角坐标系xOy中，我们把以抛物线 $y = x^{2}$ 上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”．

如图，已知某条“子抛物线”的二次项系数为 $\frac{3}{2}$ ，且与y轴交于点C ．设点A的横坐标为m（m＞0），过点A作y轴的垂线交y轴于点B ．

(1)、当m=1时，求这条“子抛物线”的解析式；

(2)、用含m的代数式表示∠ACB的余切值；

(3)、如果∠OAC=135°，求m的值．

查看试题解析
25. 如图，已知 $△ A B C$ 中， $A B = 8$ ， $B C = 10$ ， $A C = 12$ ，D是AC边上一点，且 $A B^{2} = A D \cdot A C$ ，联结BD，点E、F分别是BC、AC上两点（点E不与B、C重合）， $∠ A E F = ∠ C$ ，AE与BD相交于点G．

(1)、求证：BD平分 $∠ A B C$ ；

(2)、设 $B E = x$ ， $C F = y$ ，求 $y$ 与 $x$ 之间的函数关系式；

(3)、联结FG，当 $△ G E F$ 是等腰三角形时，求BE的长度．

查看试题解析