山东省枣庄市市中区2021年中考数学一模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. a的相反数为-3,则a等于( )A、-3 B、3 C、 D、2. 据央视网消息,全国广大共产党员积极响应党中央号召,踊跃捐款,表达对新冠肺炎疫情防控工作的支持,据统计,截至2020年3月26日,全国已有7901万多名党员自愿捐款,共捐款82.6亿元,82.6亿用科学记数法可表示为( )A、 B、 C、 D、3. 下列各运算中,计算正确的是( )A、 B、 C、 D、4. 已知一次函数y =(2m+1)x+m-3的图像不经过第二象限,则m的取值范围( )A、m>- B、m<3 C、- <m<3 D、- <m≤35. 如图,将直尺与含30°角的三角尺叠放在一起,若∠1=40°,则∠2的大小是( )
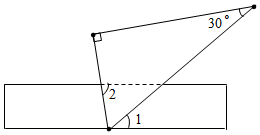 A、40° B、60° C、70° D、80°6. 如图, 中, ,则 的度数为( )
A、40° B、60° C、70° D、80°6. 如图, 中, ,则 的度数为( )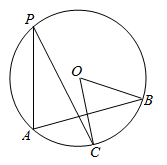 A、 B、 C、 D、7. 如图,Rt△ABC中,∠C=90°,∠B=30°,∠BAC的平分线AD交BC于点D , CD ,则BD的长是( )
A、 B、 C、 D、7. 如图,Rt△ABC中,∠C=90°,∠B=30°,∠BAC的平分线AD交BC于点D , CD ,则BD的长是( ) A、2 B、2 C、3 D、38. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )
A、2 B、2 C、3 D、38. 如图,点B在反比例函数 ( )的图象上,点C在反比例函数 ( )的图象上,且 轴, ,垂足为点C , 交y轴于点A , 则 的面积为 ( )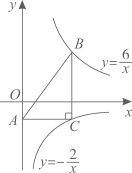 A、3 B、4 C、5 D、69. 如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )
A、3 B、4 C、5 D、69. 如图,△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( ) A、50° B、70° C、110° D、120°10. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
A、50° B、70° C、110° D、120°10. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( ) A、 B、 C、 D、11. 在平面直角坐标系 中,对于横、纵坐标相等的点称为“好点”.下列函数的图象中不存在“好点”的是( )A、 B、 C、 D、12. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
A、 B、 C、 D、11. 在平面直角坐标系 中,对于横、纵坐标相等的点称为“好点”.下列函数的图象中不存在“好点”的是( )A、 B、 C、 D、12. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:①ac<0;
②4a﹣2b+c>0;
③当x>2时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的结论有( )
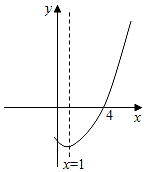 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
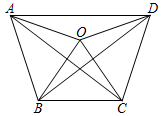
13. 因式分解: .14. 关于 的一元二次方程 有实数根,则实数 的取值范围是.15. 匈牙利著名数学家爱尔特希(P. Erdos,1913-1996)曾提出:在平面内有n个点,其中每三个点都能构成等腰三角形,人们将具有这样性质的n个点构成的点集称为爱尔特希点集.如图,是由五个点A、B、C、D、O构成的爱尔特希点集(它们为正五边形的任意四个顶点及正五边形的中心构成),则 的度数是.
 16. 如图是某商场营业大厅自动扶梯示意图.自动扶梯 的倾斜角为 ,在自动扶梯下方地面 处测得扶梯顶端 的仰角为 , 、 之间的距离为4 . 则自动扶梯的垂直高度 = .(结果保留根号)
16. 如图是某商场营业大厅自动扶梯示意图.自动扶梯 的倾斜角为 ,在自动扶梯下方地面 处测得扶梯顶端 的仰角为 , 、 之间的距离为4 . 则自动扶梯的垂直高度 = .(结果保留根号)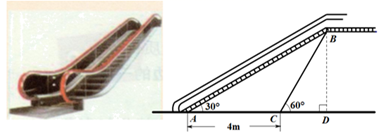 17. 如图,菱形 的边长为4, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 两点,直线 交 于点 ,连接 ,则 的长为.
17. 如图,菱形 的边长为4, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 两点,直线 交 于点 ,连接 ,则 的长为. 18. 如图,在△ABC中,CA=CB , ∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF , 点C恰在弧EF上,则图中阴影部分的面积为 .
18. 如图,在△ABC中,CA=CB , ∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF , 点C恰在弧EF上,则图中阴影部分的面积为 .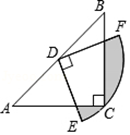
三、解答题
-
19. 化简式子 (x ),从0、1、2中取一个合适的数作为x的值代入求值.20. 在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全同学共通过多少次电话呢?我们可以用下面的方式来解决问题.用点 分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:
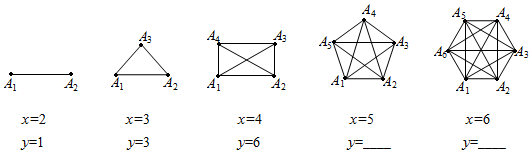 (1)、填写上图中第四个图中y的值为 , 第五个图中y的值为.(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当 时,对应的 .(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?21. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图:
(1)、填写上图中第四个图中y的值为 , 第五个图中y的值为.(2)、通过探索发现,通电话次数y与该班级人数x之间的关系式为 , 当 时,对应的 .(3)、若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?21. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图: (1)、本次随机调查的学生人数为人;(2)、补全条形统计图;(3)、若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;(4)、七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.22. 如图,在平面直角坐标系中,一次函数 的图象与x轴,y轴的交点分别为点A,点B,与反比例函数 的图象交于C,D两点, 轴于点E,连接 , .
(1)、本次随机调查的学生人数为人;(2)、补全条形统计图;(3)、若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;(4)、七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.22. 如图,在平面直角坐标系中,一次函数 的图象与x轴,y轴的交点分别为点A,点B,与反比例函数 的图象交于C,D两点, 轴于点E,连接 , .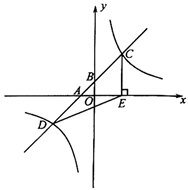 (1)、求反比例函数的解析式;(2)、求 的面积.23. 如图,已知边长为10的正方形 是 边上一动点(与 不重合),连结 是 延长线上的点,过点E作 的垂线交 的角平分线于点F,若 .
(1)、求反比例函数的解析式;(2)、求 的面积.23. 如图,已知边长为10的正方形 是 边上一动点(与 不重合),连结 是 延长线上的点,过点E作 的垂线交 的角平分线于点F,若 . (1)、求证: ;(2)、若 ,求 的面积;(3)、请直接写出 为何值时, 的面积最大.24. 如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D , 过D作BC的垂线,垂足为E .
(1)、求证: ;(2)、若 ,求 的面积;(3)、请直接写出 为何值时, 的面积最大.24. 如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D , 过D作BC的垂线,垂足为E .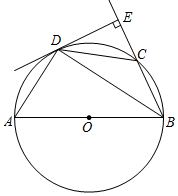 (1)、求证:DE与⊙O相切;(2)、若AB=5,BE=4,求BD的长;25. 如图,抛物线y=x2+bx+c与x轴交于A(一1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
(1)、求证:DE与⊙O相切;(2)、若AB=5,BE=4,求BD的长;25. 如图,抛物线y=x2+bx+c与x轴交于A(一1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).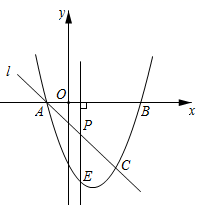 (1)、求抛物线的解析式.(2)、点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.(3)、点F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
(1)、求抛物线的解析式.(2)、点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.(3)、点F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.