山东省烟台市福山区2021年中考数学4月模拟试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 下列实数中,分数是( )A、π B、 C、 D、-1.22. 下列窗花图案中,是轴对称图形不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、
3. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、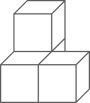 B、
B、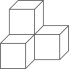 C、
C、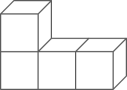 D、
D、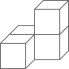 4. 若关于x的分式方程 有增根,则a的值为( )A、−3 B、3 C、2 D、5. 小亮要计算一组数据80,82,74,86,79的方差 ,在计算平均数的过程中,将这组数据中的每一个数都减去80,得到一组新数据0,2,-6,6,-1,记这组新数据的方差为 ,则 与 的大小关系为( )A、 B、 C、 D、无法确定6. 关于x的一元二次方程 的一个根是0,则 的值是( )A、−3或1 B、1 C、−3 D、7. 如图,AB是⊙O的弦,作OC⊥OA交⊙O的切线BC于点C , 交AB于点D . 已知∠OAB=20°,则∠OCB的度数为( )
4. 若关于x的分式方程 有增根,则a的值为( )A、−3 B、3 C、2 D、5. 小亮要计算一组数据80,82,74,86,79的方差 ,在计算平均数的过程中,将这组数据中的每一个数都减去80,得到一组新数据0,2,-6,6,-1,记这组新数据的方差为 ,则 与 的大小关系为( )A、 B、 C、 D、无法确定6. 关于x的一元二次方程 的一个根是0,则 的值是( )A、−3或1 B、1 C、−3 D、7. 如图,AB是⊙O的弦,作OC⊥OA交⊙O的切线BC于点C , 交AB于点D . 已知∠OAB=20°,则∠OCB的度数为( ) A、20° B、30° C、40° D、50°8. 如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:①作线段 ,分别以 , 为圆心,以 长为半径作弧,两弧的交点为 ;②以 为圆心,仍以 长为半径作弧交 的延长线于点 ;③连接 , .下列结论错误的是( )
A、20° B、30° C、40° D、50°8. 如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:①作线段 ,分别以 , 为圆心,以 长为半径作弧,两弧的交点为 ;②以 为圆心,仍以 长为半径作弧交 的延长线于点 ;③连接 , .下列结论错误的是( )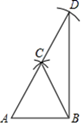 A、 B、点 是 的外心 C、 D、9.
A、 B、点 是 的外心 C、 D、9.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数是( )
 A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣210. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )
A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣210. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )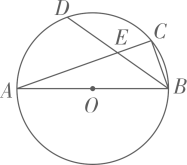 A、 B、 C、 D、11. 如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿 的方向运动,到达点C时停止,设运动时间为x(秒), ,则y关于x的函数的图象大致为( )
A、 B、 C、 D、11. 如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿 的方向运动,到达点C时停止,设运动时间为x(秒), ,则y关于x的函数的图象大致为( ) A、
A、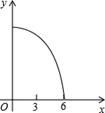 B、
B、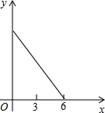 C、
C、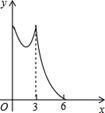 D、
D、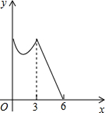
二、填空题
-
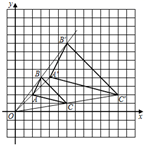
12. =13. 若等式y= 成立,则x的取值范围是 .14. 截至2021年3月29日,全国各地累计报告接种新冠病毒疫苗11096.2万剂次,则11096.2万用科学记数法表示为 .15. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,若点A(2,2),B(3,4),C(6,1),B'(6,8),则△A'B'C'的面积为 .
 16. 如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径 与线段AD、A′D围成的阴影部分面积是.
16. 如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径 与线段AD、A′D围成的阴影部分面积是.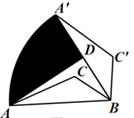 17. 如图,矩形 的顶点A、C分别在x轴、y轴上, ,将 绕点O顺时针旋转,点B落在y轴上的点D处,得到 , 交 于点G,若反比例函数 的图象经过点G,则k的值为.
17. 如图,矩形 的顶点A、C分别在x轴、y轴上, ,将 绕点O顺时针旋转,点B落在y轴上的点D处,得到 , 交 于点G,若反比例函数 的图象经过点G,则k的值为.
三、解答题
-
18. 先化简,再求值: ,其中19. 2021年3月29日,卫建委发布了《新冠疫苗接种指南》,某中学为了解九年级学生对新冠疫苗知识的了解情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类﹣﹣非常了解;B类﹣﹣比较了解;C类﹣﹣般了解;D类﹣﹣不了解.现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
 (1)、本次共调查了 ▲ 名学生;补全条形统计图;(2)、D类所对应扇形的圆心角的大小为;若该校九年级学生共有1000名,根据以上抽样结果,估计该校九年级学生对新冠疫苗知识非常了解的约有名.(3)、已知调查的该班第一组学生中有2名男生1名女生,老师随机从该组中选取2名学生进一步了解其家庭成员接种情况.请用树状图或列表求所选2名学生恰为一男生一女生的概率.20. 鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为 ,无人机沿水平线 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段 的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中 米.
(1)、本次共调查了 ▲ 名学生;补全条形统计图;(2)、D类所对应扇形的圆心角的大小为;若该校九年级学生共有1000名,根据以上抽样结果,估计该校九年级学生对新冠疫苗知识非常了解的约有名.(3)、已知调查的该班第一组学生中有2名男生1名女生,老师随机从该组中选取2名学生进一步了解其家庭成员接种情况.请用树状图或列表求所选2名学生恰为一男生一女生的概率.20. 鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为 ,无人机沿水平线 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段 的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中 米. (1)、求无人机的飞行高度 ;(结果保留根号)(2)、求河流的宽度 .(结果精确到1米,参考数据: )21. 某电商积极响应市政府号召,在线销售甲、乙、丙三种农产品.已知 乙产品的售价比 甲产品的售价多5元, 丙产品的售价是 甲产品售价的3倍,用270元购买丙产品的数量是用60元购买乙产品数量的3倍.(1)、求甲、乙、丙三种农产品每千克的售价分别是多少元?(2)、电商推出如下销售方案:甲、乙、丙三种农产品搭配销售共 ,其中乙产品的数量是丙产品数量的2倍,且甲、丙两种产品数量之和不超过乙产品数量的3倍.请你帮忙计算,按此方案购买 农产品最少要花费多少元?22. 如图,在Rt△ 中, , 平分∠ , 交 于点 ,△ 的外接圆⊙ 与边 相交于点 ,过点 作 的垂线交 于 ,交 于 ,交⊙ 于点 ,连接 .
(1)、求无人机的飞行高度 ;(结果保留根号)(2)、求河流的宽度 .(结果精确到1米,参考数据: )21. 某电商积极响应市政府号召,在线销售甲、乙、丙三种农产品.已知 乙产品的售价比 甲产品的售价多5元, 丙产品的售价是 甲产品售价的3倍,用270元购买丙产品的数量是用60元购买乙产品数量的3倍.(1)、求甲、乙、丙三种农产品每千克的售价分别是多少元?(2)、电商推出如下销售方案:甲、乙、丙三种农产品搭配销售共 ,其中乙产品的数量是丙产品数量的2倍,且甲、丙两种产品数量之和不超过乙产品数量的3倍.请你帮忙计算,按此方案购买 农产品最少要花费多少元?22. 如图,在Rt△ 中, , 平分∠ , 交 于点 ,△ 的外接圆⊙ 与边 相交于点 ,过点 作 的垂线交 于 ,交 于 ,交⊙ 于点 ,连接 . (1)、求证:BC是⊙O的切线;(2)、若sin∠G= ,AB=16,求⊙O的直径.23. 在△ABC中,∠BAC=90°,AB=AC , 点D在边BC上,DE⊥DA且DE=DA , AE交边BC于点F , 连接CE .
(1)、求证:BC是⊙O的切线;(2)、若sin∠G= ,AB=16,求⊙O的直径.23. 在△ABC中,∠BAC=90°,AB=AC , 点D在边BC上,DE⊥DA且DE=DA , AE交边BC于点F , 连接CE .
(特例发现)
(1)、如图1,当AD=AF时,①求证:BD=CF;
②推断:∠ACE= ▲ °;
(2)、(探究证明)如图2,当AD≠AF时,请探究∠ACE的度数是否为定值,并说明理由.
24. 如图1,抛物线 与 轴交于 , 两点,与 轴交于点 .直线 经过抛物线上两点 , .已知点 , 的横坐标分别为 , 且满足 ,直线 的表达式为 . (1)、求 的值及抛物线的表达式;(2)、设点 是直线 上一动点,问:点 在什么位置上时, 的周长最小?求出点 的坐标及 周长的最小值;(3)、如图2, 是线段 上的一个动点,过点 作垂直于 轴的直线与直线 和抛物线分别交于点 , .若点 是直线 上一个动点,当点 恰好是线段 的中点时,在坐标平面内是否存在点 ,使以点 , , , 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求 的值及抛物线的表达式;(2)、设点 是直线 上一动点,问:点 在什么位置上时, 的周长最小?求出点 的坐标及 周长的最小值;(3)、如图2, 是线段 上的一个动点,过点 作垂直于 轴的直线与直线 和抛物线分别交于点 , .若点 是直线 上一个动点,当点 恰好是线段 的中点时,在坐标平面内是否存在点 ,使以点 , , , 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.