山东省济南市章丘区2021年中考数学一模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 2021的倒数是( )A、 2021 B、-2021 C、 D、2. 数据720000用科学记数法表示为( )A、0.72×104 B、7.2×105 C、72×105 D、7.2×1063. 下面计算正确的是( )A、a3•a3=2a3 B、2a2+a2=3a4 C、a9÷a3=a3 D、(﹣3a2)3=﹣27a64. 如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
 A、80° B、85° C、90° D、95°5. 为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表:
A、80° B、85° C、90° D、95°5. 为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表:锻炼时间(时)
3
4
5
6
7
人数(人)
6
13
14
5
2
这40名居民一周体育锻炼时间的众数和中位数是( )
A、14,5 B、14,6 C、5,5 D、5,66. 如图,OA交⊙O于点B , AD切⊙O于点D , 点C在⊙O上.若∠A=40°,则∠C为( ) A、20° B、25° C、30° D、35°7. 一个不透明的盒子中装有1个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为( )A、 B、 C、 D、8. 化简 得( )A、 B、 C、 D、9. 如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按逆时针方向旋转90°后,得到△A'B'C′,则点A′的坐标是( )
A、20° B、25° C、30° D、35°7. 一个不透明的盒子中装有1个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为( )A、 B、 C、 D、8. 化简 得( )A、 B、 C、 D、9. 如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按逆时针方向旋转90°后,得到△A'B'C′,则点A′的坐标是( ) A、(5,1) B、(5,﹣1) C、(﹣1,5) D、(1,﹣5)10. 已知二次函数y=ax2+bx+c的图象如图所示,则在同一直角坐标系中,一次函数y=ax+b和反比例函数 的图象大致是( )
A、(5,1) B、(5,﹣1) C、(﹣1,5) D、(1,﹣5)10. 已知二次函数y=ax2+bx+c的图象如图所示,则在同一直角坐标系中,一次函数y=ax+b和反比例函数 的图象大致是( )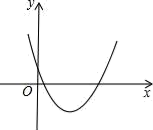 A、
A、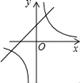 B、
B、 C、
C、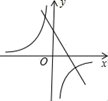 D、
D、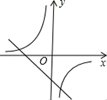 11. 保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的 同一水平线的 处,测得 米,沿坡度 的斜坡 走到 点,测得塔顶 仰角为37°,再沿水平方向走20米到 处,测得塔顶 的仰角为22°,则塔高 为( )米.(结果精确到十分位)( , , , , , )
11. 保利观澜旁边有一望江公园,公园里有一文峰塔,工程人员在与塔底中心的 同一水平线的 处,测得 米,沿坡度 的斜坡 走到 点,测得塔顶 仰角为37°,再沿水平方向走20米到 处,测得塔顶 的仰角为22°,则塔高 为( )米.(结果精确到十分位)( , , , , , ) A、18.3米 B、19.3米 C、20米 D、21.2米12. 已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )
A、18.3米 B、19.3米 C、20米 D、21.2米12. 已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )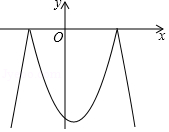 A、﹣ <m<3 B、﹣ <m<2 C、﹣2<m<3 D、﹣6<m<﹣2
A、﹣ <m<3 B、﹣ <m<2 C、﹣2<m<3 D、﹣6<m<﹣2二、填空题
-
13. 分解因式:x3﹣25x=.14. 若x,y满足方程组 则 的值为.15. 一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是.16. 如图,已知扇形的圆心角为 ,半径为1,那么该扇形的弧长为 . (结果保留 )
 17. 如图,一辆汽车和一辆摩托车分别从A , B两地去同一城市C , 它们离A地的路程随时间变化的图象如图所示,则两车相遇时距离C地还有千米.
17. 如图,一辆汽车和一辆摩托车分别从A , B两地去同一城市C , 它们离A地的路程随时间变化的图象如图所示,则两车相遇时距离C地还有千米. 18. 如图,在正方形ABCD中, ,P为平面内任意一点, ,连接PD , 将线段PD绕着点D顺时针旋转 ,得到线段DQ , 连接CQ , 则 的最小值为 .
18. 如图,在正方形ABCD中, ,P为平面内任意一点, ,连接PD , 将线段PD绕着点D顺时针旋转 ,得到线段DQ , 连接CQ , 则 的最小值为 .
三、解答题
-
19. 计算: .20. 解不等式组: ,并写出它的所有整数解.21. 如图,AB∥CD , E、F分别为AB、CD上的点,且EC∥BF , 连接AD , 分别与EC、BF相交于点G、H , 若AB=CD , 求证:AG=DH .
 22. 2020年疫情期间,某校为学生提供四种在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了解学生的需求,对学生进行了“你最喜欢哪种在线学习方式的调查,调查结果制成两幅不完整统计图如图,根据图中信息回答问题:
22. 2020年疫情期间,某校为学生提供四种在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了解学生的需求,对学生进行了“你最喜欢哪种在线学习方式的调查,调查结果制成两幅不完整统计图如图,根据图中信息回答问题: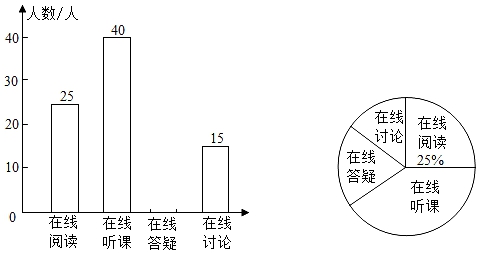 (1)、本次调查人数有人,在线答疑所在扇形的圆心角度数是;(2)、补全条形统计图;(3)、甲、乙两位同学都参加了在线学习,请用画树状图或列表的方法求出两名同学喜欢同一种在线学习方式的概率.23. 已知在Rt△ABC中,∠C=90°;以斜边AB上的一点O为圆心作圆O,与AC、BC分别相切与点D、E.
(1)、本次调查人数有人,在线答疑所在扇形的圆心角度数是;(2)、补全条形统计图;(3)、甲、乙两位同学都参加了在线学习,请用画树状图或列表的方法求出两名同学喜欢同一种在线学习方式的概率.23. 已知在Rt△ABC中,∠C=90°;以斜边AB上的一点O为圆心作圆O,与AC、BC分别相切与点D、E.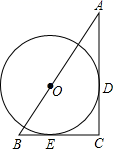 (1)、求证:CD=CE;(2)、若AC=8,AB=10;求AD的长.24. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?25. 如图1,在平面直角坐标系中,直线AB与反比例函数 的图象交于点A (1,3)和点B (3, n),与x轴交于点C,与y轴交于点D.
(1)、求证:CD=CE;(2)、若AC=8,AB=10;求AD的长.24. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?25. 如图1,在平面直角坐标系中,直线AB与反比例函数 的图象交于点A (1,3)和点B (3, n),与x轴交于点C,与y轴交于点D.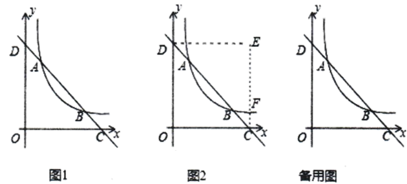 (1)、求反比例函数的表达式及n的值;(2)、将△OCD沿直线AB翻折,点O落在第一象限内的点E处, EC与反比例函数的图象交于点F.
(1)、求反比例函数的表达式及n的值;(2)、将△OCD沿直线AB翻折,点O落在第一象限内的点E处, EC与反比例函数的图象交于点F.①请求出点F的坐标;
②在x轴上是否存在点P,使得△DPF是以DF为斜边的直角三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
26. 如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.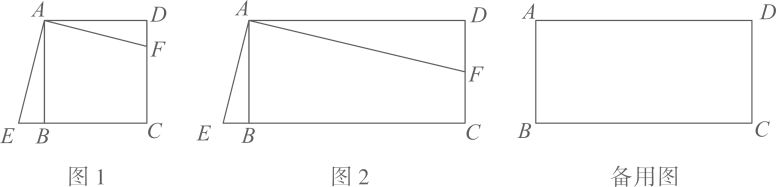 (1)、如图1,若k=1,则AF与AE之间的数量关系是;(2)、如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)(3)、若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.27. 如图,已知抛物线 与 轴相交于 , ,与 轴相交于点 ,直线 ,垂足为 .
(1)、如图1,若k=1,则AF与AE之间的数量关系是;(2)、如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)(3)、若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.27. 如图,已知抛物线 与 轴相交于 , ,与 轴相交于点 ,直线 ,垂足为 . (1)、求该抛物线的表达式:(2)、若直线 与该抛物线的另一个交点为 ,求点 的坐标;(3)、设动点 在该抛物线上,当 时,求 的值.
(1)、求该抛物线的表达式:(2)、若直线 与该抛物线的另一个交点为 ,求点 的坐标;(3)、设动点 在该抛物线上,当 时,求 的值.