辽宁省抚顺市新抚区2021年中考数学五模试卷

试卷更新日期：2021-07-28 类型：中考模拟

进入出卷网下载

一、单选题

1. －5的绝对值等于（）

A、－5 B、5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、﹣x²﹣3x＝﹣4x B、2x×4x³＝8x⁴ C、（﹣a²b）³＝a⁶b³ D、a²b÷（﹣ab²）＝﹣ab

查看试题解析
4. 如图所示的几何体，它的左视图正确的是（）

A、 B、 C、 D、

查看试题解析
5. 商场经理调查了本商场某品牌女鞋一个月内不同尺码的销售量，如表：

尺码/码

36

37

38

39

40

数量/双

15

28

13

9

5

商场经理最关注这组数据的（）

A、众数 B、平均数 C、中位数 D、方差

查看试题解析
6. 如图，若AB∥DE ， ∠B＝135°，∠D＝30°，则∠C的度数为（）

A、70° B、75° C、80° D、85°

查看试题解析
7. 如图所示，阴影是两个相同菱形的重合部分，一个小球随机的在图案上滚动，最后停留在阴影部分的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{7}$ C、 $\frac{1}{8}$ D、 $\frac{1}{9}$

查看试题解析
8. 下列命题正确的是（）

A、一组邻边相等的四边形是菱形 B、对角线互相平分的四边形是菱形 C、对角线互相垂直的四边形是菱形 D、四条边都相等的四边形是菱形

查看试题解析
9. 不等式组 ${\begin{matrix} - 2 x + 5 \geq 3 \\ \frac{x - 1}{2} < \frac{x}{3} \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在△ABC中，AC＝BC ， ∠ACB＝90°，S_△ABC＝4cm² ．正方形CDEF的顶点D ， F分别在AC ， BC边上，设CD＝CF＝x ， △ABC与正方形CDEF重叠部分的面积为y ，则下列图象中能表示y与x之间的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 新型冠状病毒颗粒的平均直径约为 $0.000012 c m$ ，数据 $0.000012$ 用科学记数法表示为．

查看试题解析
12. 计算： ${(- \frac{1}{2})}^{- 1} - \sqrt[3]{- 8} =$ ．

查看试题解析
13. 如图，已知直线AB和CD相交于O点，∠COE是直角，OF平分∠AOE ， ∠COF=34°，则∠BOD的度数为．

查看试题解析
14. 关于x的一元二次方程 $(m - 1) x^{2} - 2 x + 1 = 0$ 有实数根，则m的取值范围是．

查看试题解析
15. 八年级某同学5次数学小测验的成绩分别为90分，85分，95分，90分，85分，则该同学这5次成绩的平均分是．

查看试题解析
16. 如图，在矩形ABCD中，AB＝2AD＝6，点P为AB边上一点，且AP≤3，连接DP ，将△ADP沿DP折叠，点A落在点M处，连接CM，BM ，当 $△ B C M$ 为等腰三角形时，AP的长为．

查看试题解析
17. 如图，直线 $y = \frac{1}{2} x - 1$ 与x轴交于点B ，与y轴交于点C ，与双曲线 $y = \frac{k}{x}$ 在第一象限的分支交于点A ，且AB=BC ，则k 等于．

查看试题解析
18. 如图，在△ABC中，AB＞AC ， AE平分∠BAC ， BD⊥AE于D ， CE⊥AE于E ， F为BC的中点，给出结论：①FD∥AC；②FE＝FD；③AB﹣AC＝ $\sqrt{2}$ DE；④∠BAC+∠DFE＝180°．其中正确结论的题号是．

查看试题解析

三、解答题

19. 先化简，再求值： $(\frac{2 x^{2} + 2 x}{x^{2} - 1} - \frac{x^{2} - x}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1}$ ，其中 $x = 1 + \sqrt{2}$ .

查看试题解析
20. 随着经济的快速发展，环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况，随机调查了部分学生，调查结果分为“非常了解”“了解”“了解较少”“不了解”四类，并将调查结果绘制成下面两幅统计图.

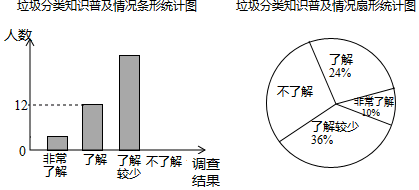(1)、求：本次被调查的学生有多少名？补全条形统计图.

(2)、估计该校1200名学生中“非常了解”与“了解”的人数和是多少.

(3)、被调查的“非常了解”的学生中有2名男生，其余为女生，从中随机抽取2人在全校做垃圾分类知识交流，请利用画树状图或列表的方法，求恰好抽到一男一女的概率.

查看试题解析
21. 平高集团有限公司准备生产甲、乙两种开关，共8万件，销往东南亚国家和地区。已知2件甲种开关与3件乙种开关销售额相同；3件甲种开关比2件乙种开关的销售额多1500元。

(1)、甲种开关与乙种开关的销售单价各为多少元?

(2)、若甲、乙两种开关的销售总收入不低于5400万元，则至少销售甲种开关多少万件？

查看试题解析
22. 如图，AC与⊙O相切，切点为C ，点B在CO的延长线上，BD⊥AO ，垂足为D ， ∠ABD=∠BOD．

(1)、求证：AB为⊙O的切线；

(2)、若BC=4，AC=3，求BD的长．

查看试题解析
23. 如图，一艘轮船位于灯塔P的北偏东75°方向，距离灯塔60海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处．这时，B处距离灯塔P有多远（结果取整数）？（参考数据 $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 某驻村扶贫小组实施产业扶贫，帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克，规定销售单价不低于成本，又不高于成本的两倍.经过市场调查发现，某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示：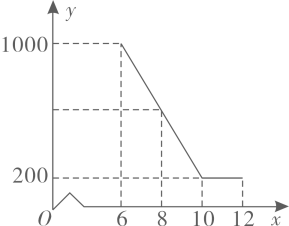

(1)、求y与x的函数解析式(也称关系式)；

(2)、求这一天销售西瓜获得的利润的最大值.

查看试题解析
25. 如图，P为正方形ABCD对角线BD所在直线上的动点，连接CP ，将CP绕点C逆时针旋转90°得线段CQ ，连接DQ ， DQ与直线AC相交于点M ， AC与BD相交于点O ．

(1)、求证：PD=2OM；

(2)、当P在直线BD上运动时，探究线段OP ， OM ， CM的数量关系，直接写出探究结论；

(3)、若AB=4，DQ=6，直接写出AM的长．

查看试题解析
26. 如图，直线 $y = - \frac{\sqrt{3}}{3} x + 3$ 与x轴交于点A ，与y轴交于点B ，抛物线 $y = - \frac{1}{3} x^{2} + b x + c$ 经过点A ， B两点，与x轴负半轴交于点C．

(1)、求抛物线的解析式；

(2)、点P在抛物线上，∠PBA=15°，求点P的横坐标；

(3)、点M在射线AB上，点N在射线AC上，∠BNM=30°，D在坐标平面内，当以B ， D ， M ， N为顶点的四边形为菱形时，直接写出点D的坐标．

查看试题解析

尺码/码	36	37	38	39	40
数量/双	15	28	13	9	5