辽宁省抚顺市2021年中考数学四模试卷

试卷更新日期：2021-07-28 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{2}{3}$ 的相反数是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $- \frac{3}{2}$

查看试题解析
2. 计算 $x^{6} \div x^{2} (x \neq 0)$ 的结果是（）

A、 $x^{3}$ B、 $x^{- 3}$ C、 $x^{4}$ D、 $x^{- 4}$

查看试题解析
3. 在下列几何体中，主视图是矩形的是（）

A、 B、 C、 D、

查看试题解析
4. 我国珠港澳大桥闻名世界，它东起香港国际机场附近的香港口岸人工岛，向西横跨南海伶仃洋水域接珠海和澳门人工岛，止于珠海洪湾立交，工程项目总投资1269亿元．用科学记数法表示1269亿正确的是（）

A、 $1.269 \times 10^{3}$ B、 $1.269 \times 10^{4}$ C、 $1.269 \times 10^{11}$ D、 $1.269 \times 10^{12}$

查看试题解析
5. 已知点 $A (x_{1} ， m)$ ， $B (x_{2} ， n)$ 都在反比例函数 $y = - \frac{2}{x}$ 图象上，且 $0 < x_{1} < x_{2}$ 则m，n的大小关系是（）

A、 $m > n$ B、 $m = n$ C、 $m \leq n$ D、 $m < n$

查看试题解析
6. 如图，在 $▱ A B C D$ 中，将 $△ A D C$ 沿AC折叠后，点D恰好落在DC的延长线上的点E处．若 $∠ B = 60 °$ ， $A B = 3$ ，则 $△ A D E$ 的周长为（）

A、12 B、15 C、18 D、21

查看试题解析
7. 如图，在4×4的正方形网格中，若将 $△ A B C$ 绕着点A逆时针旋转得到 $△ A B^{'} C^{'}$ ，则 $\overset{⌢}{B B^{'}}$ 的长为（）

A、 $π$ B、 $\frac{π}{2}$ C、 $7 π$ D、 $6 π$

查看试题解析
8. 某商品原价为100元，第一次涨价40%，第二次在第一次的基础上又涨价10%，设平均每次增长的百分数为 $x$ ，那么 $x$ 应满足的方程是（）

A、 $x = \frac{40 % + 1096}{2}$ B、 $100 (1 + 40 %) (1 + 10 %) = {(1 + x)}^{2}$ C、 $(1 + 40 %) (1 + 10 %) = {(1 + x)}^{2}$ D、 $(100 + 40 %) (100 + 10 %) = 100 {(1 + x)}^{2}$

查看试题解析
9. 已知关于 $x$ 的分式方程 $\frac{x}{x - 1} - 2 = \frac{k}{x - 1}$ 的解为正数，则 $k$ 的取值范围为（）

A、 $- 2 < k < 0$ B、 $k > - 2$ 且 $k \neq - 1$ C、 $k > - 2$ D、 $k < 2$ 且 $k \neq 1$

查看试题解析
10. 如图，在矩形ABCD中， $AB = 4$ ， $BC = 6$ ，当直角三角板MPN的直角顶点P在BC边上移动时，直角边MP始终经过点A，设直角三角板的另一直角边PN与CD相交于点 $Q . BP = x$ ， $CQ = y$ ，那么y与x之间的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 函数y＝ $\frac{\sqrt{1 - x}}{x - 1}$ 的自变量x的取值范围是．

查看试题解析
12. 现有四张正面分别标有数字﹣1，1，2，3的不透明卡片，它们除数字外其余完全相同，将它们背而面朝上洗均匀，随机抽取一张，记下数字后放回，背面朝上洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为m ， n ，则点P（m ， n）在第二象限的概率为．

查看试题解析
13. 不等式组 ${\begin{array}{l} x - 3 < 0 \\ \frac{x + 4}{2} \geq 1 \end{array}$ 的解集为．

查看试题解析
14. 如果关于x的一元二次方程x²﹣4x+k=0有实数根，那么k的取值范围是.

查看试题解析
15. 如图，平面直角坐标系中，点A、B分别是x、y轴上的动点，以AB为边作边长为2的正方形ABCD，则OC的最大值为

查看试题解析
16. 双曲线y₁ ， y₂在第一象限的图象如图，已知y₁＝ $\frac{4}{x}$ ，过y₁上的任意一点A作x轴的平行线交y₂于点B，交y轴于点C，若S_△_AOB＝ $\frac{1}{2}$ ，则y₂的表达式是.

查看试题解析
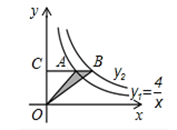17. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，BC＝6，点D是BC边上一动点（不与B、C重合），过点D作DE⊥BC交AB边于点E，将∠B沿直线DE翻折，点B落在射线BC上的点F处，当△AEF为直角三角形时，BD的长为．

查看试题解析
18. 如图，已知 $△ A B C$ 是等边三角形，点D，E分别在边BC，AC上，且 $C D = C E$ ，连接DE并延长至点F，使 $E F = A E$ ，连接AF，CF，连接E并延长交CF于点G．下列结论：
① $△ A B E ≌ △ A C F$ ；② $B C = D F$ ；③ $S_{△ A B C} = S_{△ A C F} + S_{△ D C F}$ ；④若 $B D = 2 D C$ ，则 $C F = 2 E C$ ．其中正确的结论是．（填写所有正确结论的序号）

查看试题解析

三、解答题

19. 先化简，再求值： $(x + 2 + \frac{3}{x - 2}) \div \frac{1 + 2 x + x^{2}}{x - 2}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
20. 为了遏制新型冠状病毒疫情的蔓延势头，各地教育部门在推迟各级学校开学时间的同时提出“停课不停学”的要求，各地学校也都开展了远程网络教学，某校为学生提供四类在线学习方式：在线阅读、在线听课、在线答疑在线讨论，为了了解学生的需求，该校通过网络对本校部分学生进行了“你对哪类在线学校方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图

(1)、本次调查的人数有多少人？

(2)、请补全条形图；

(3)、请求出“在线答疑”在扇形图中的圆心角度数；

(4)、小宁和小娟都参加了远程网络教学活动，请求出小宁和小娟选择同一种学习方式的概率．

查看试题解析
21. 为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两种玩具，其中A类玩具的进价比B玩具的进价每个多3元，经调查：用900元购进A类玩具的数量与用750元购进B类玩具的数量相同

(1)、求A、B两类玩具的进价分别是每个多少元？

(2)、该玩具店共购进了A、B两类玩具共100个，若玩具店将每个A类玩具定价为30元出售，每个B类玩具定价25元出售，且全部售出后所获得利润不少于1080元，则商店至少购进A类玩具多少个？

查看试题解析
22. 如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°.连接AO并延长，交⊙O于点D，连接BD.过点C作⊙O的切线，与BA的延长线相交于点E.

(1)、求证：AD∥EC；

(2)、若AB＝12，求线段EC的长.

查看试题解析
23. 因东坡文化远近闻名的遗爱湖公园，“国庆黄金周”期间，游人络绎不绝，现有一艘游船载着游客在遗爱湖中游览．当船在A处时，船上游客发现岸上 $P_{1}$ 处的临皋亭和 $P_{2}$ 处的遗爱亭都在东北方向；当游船向正东方向行驶 $600 m$ 到达B处时，游客发现遗爱亭在北偏西15°方向；当游船继续向正东方向行驶 $400 m$ 到达C处时，游客发现临皋亭在北偏西60°方向．

(1)、求A处到临皋亭P处的距离．

(2)、求临皋亭 $P_{1}$ 处与遗爱亭 $P_{2}$ 处之间的距离（计算结果保留根号）

查看试题解析
24. 超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件.根据市场调查发现，销售单价每增加2元，每天销售量会减少1件.设销售单价增加 $x$ 元，每天售出 $y$ 件.

(1)、请写出 $y$ 与 $x$ 之间的函数表达式；

(2)、当 $x$ 为多少时，超市每天销售这种玩具可获利润2250元？

(3)、设超市每天销售这种玩具可获利 $w$ 元，当 $x$ 为多少时 $w$ 最大，最大值是多少？

查看试题解析
25. 如图1，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 60 °$ ，D为BC边上一点（不与点B，C重合）．将线段AD绕点A逆时针旋转60°得到AE，连接EC，则：

(1)、① $∠ A C E$ 的度数是；
②线段AC，CD，CE之间的数量关系是．

(2)、如图2，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，请写出 $∠ A C E$ 的度数及线段AD，BD，CD之间的数量关系，并说明理由；

(3)、如图3，在 $R t △ D B C$ 中， $D B = 3$ ， $D C = 5$ ， $∠ B D C = 90 °$ ，若点 $A$ 满足 $A B = A C$ ， $∠ B A C = 90 °$ ，请直接写出线段AD的长度．

查看试题解析
26. 如图，抛物线y＝ $- \frac{1}{3} x^{2}$ +bx+c经过△ABC的三个顶点，其中点A（0，﹣1），点B（9，﹣10），AC∥x轴，点P是直线AC上方抛物线上的动点．

(1)、求抛物线的解析式；

(2)、过点P且与y轴平行的直线l与直线AB ， AC分别交于点E ， F ，当四边形AECP的面积最大时，求点P的坐标；

(3)、当点P为抛物线的顶点时，在直线AC上是否存在点Q ，使得以C ， P ， Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析