吉林省长春市绿园区2021年中考数学二模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 如图,数轴上被墨水遮盖的数可能是( )
 A、-3.2 B、-3 C、-2 D、-0.52. 中国高速路里程已突破120000公里,居世界第一位,将120000用科学记数法表示为( )A、0.12×106 B、1.2×105 C、12×104 D、120×1033. 下列图形中,不是正方体表面展开图的是( )A、
A、-3.2 B、-3 C、-2 D、-0.52. 中国高速路里程已突破120000公里,居世界第一位,将120000用科学记数法表示为( )A、0.12×106 B、1.2×105 C、12×104 D、120×1033. 下列图形中,不是正方体表面展开图的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知不等式组 ,其解集在数轴上表示正确的是( )A、
4. 已知不等式组 ,其解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,有一斜坡 的长 米,坡角 ,则斜坡 的铅垂高度 为( ).
5. 如图,有一斜坡 的长 米,坡角 ,则斜坡 的铅垂高度 为( ).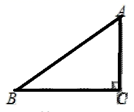 A、 B、 C、 D、6. 如图, 是 的直径, 是弦(点C不与点A , 点B重合,且点C与点D位于直径 两侧),若 ,则 等于( )
A、 B、 C、 D、6. 如图, 是 的直径, 是弦(点C不与点A , 点B重合,且点C与点D位于直径 两侧),若 ,则 等于( )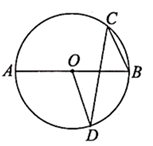 A、 B、 C、 D、7. 如图,在 中, 用直尺和圆规在边BC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )A、
A、 B、 C、 D、7. 如图,在 中, 用直尺和圆规在边BC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,矩形OABC的顶点A、C分别在x轴、y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转600得到线段OP,连接AP,反比例函数y= 过P、B两点,则k的值为( )
8. 如图,矩形OABC的顶点A、C分别在x轴、y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转600得到线段OP,连接AP,反比例函数y= 过P、B两点,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 笔记本的单价是x元,圆珠笔的单价是y元,买4本笔记本和2支圆珠笔共需元.10. 因式分解:2m2﹣2= .11. 若关于x的一元二次方程x2﹣4x+m﹣1=0有两个相等的实数根,则m的值为.12. 十二边形的内角和度数为.13. 如图,扇形 的圆心角是为 ,四边形 是边长为 的正方形,点 分别在 在弧 上,那么图中阴影部分的面积为 . (结果保留 )
 14. 在平面直角坐标系中,A点坐标为(﹣1,4),B点坐标为(5,4).已知抛物线y=x2﹣2x+c与线段AB有公共点,则c的取值范围是 .
14. 在平面直角坐标系中,A点坐标为(﹣1,4),B点坐标为(5,4).已知抛物线y=x2﹣2x+c与线段AB有公共点,则c的取值范围是 .三、解答题
-
15. 计算:|1 | (π﹣2021)0 .16. 五一期间,甲、乙两人在附近的景点游玩,甲从 两个景点中任意选择一个游玩,乙从 三个景点中任意选择一个游玩.(1)、乙恰好游玩 景点的概率为 .(2)、用列表或画树状图的方法列出甲、乙恰好游玩同一景点的所有等可能的结果.并求甲、乙恰好游玩同一景点的概率.17. 某公司打算购买一批相同数量的玻璃杯和保温杯,计划用2000元购买玻璃杯,用2800元购买保温杯.已知一个保温杯比一个玻璃杯贵10元,求一个玻璃杯的价格.18. 如图,网格中有一条线段 ,点 、 都在格点上,网格中的每个小正方形的边长为1.请在图①和图②中各画出一个格点 ,使 是直角三角形,且 ,并满足以下要求:
 (1)、在图①中画出的三角形的两条直角边的长度均为有理数(画出一个即可).(2)、在图②中画出的三角形的两条直角边的长度均为无理数(画出一个即可).(3)、满足(1)、(2)的 共有个.19. 如图,在 中,过点 作 于点 ,点 在边 上, ,连接 , .
(1)、在图①中画出的三角形的两条直角边的长度均为有理数(画出一个即可).(2)、在图②中画出的三角形的两条直角边的长度均为无理数(画出一个即可).(3)、满足(1)、(2)的 共有个.19. 如图,在 中,过点 作 于点 ,点 在边 上, ,连接 , . (1)、求证:四边形 是矩形;(2)、已知 , 是 的平分线,若 ,求 的长度.20. 某校为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)、求证:四边形 是矩形;(2)、已知 , 是 的平分线,若 ,求 的长度.20. 某校为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: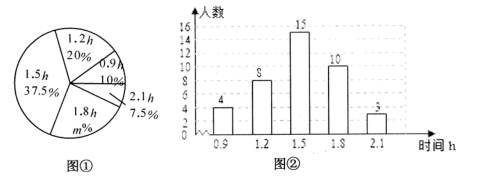 (1)、本次接受调查的初中学生人数为 , 图①中m的值为;(2)、求统计的这部分学生参加公益的时间数据的平均数、众数和中位数;(3)、根据统计的这部分学生周末参加公益时间的样本数据,若该校共有650名初中学生,估计该校在这个周末参加公益时间大于1h的学生人数.21. 甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发开往乙地,如图,线段 表示货车离甲地距离 (千米)与货车出发时间 (小时)之间的函数关系;折线 表示轿车离甲地距离 (千米)与货车出发时间 (小时)之间的函数关系,请根据图象解答下列问题:
(1)、本次接受调查的初中学生人数为 , 图①中m的值为;(2)、求统计的这部分学生参加公益的时间数据的平均数、众数和中位数;(3)、根据统计的这部分学生周末参加公益时间的样本数据,若该校共有650名初中学生,估计该校在这个周末参加公益时间大于1h的学生人数.21. 甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发开往乙地,如图,线段 表示货车离甲地距离 (千米)与货车出发时间 (小时)之间的函数关系;折线 表示轿车离甲地距离 (千米)与货车出发时间 (小时)之间的函数关系,请根据图象解答下列问题: (1)、货车的速度为千米 时;(2)、求线段 对应的函数关系式;(3)、在轿车行驶过程中,若两车的距离不超过20千米,直接写出 的取值范围.22. (教材呈现)下图是华师版九年级上册数学教材第103页的部分内容.
(1)、货车的速度为千米 时;(2)、求线段 对应的函数关系式;(3)、在轿车行驶过程中,若两车的距离不超过20千米,直接写出 的取值范围.22. (教材呈现)下图是华师版九年级上册数学教材第103页的部分内容.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证: .
证明:延长CD至点E,使DE=CD , 连结AE、BE .
 (1)、请根据教材提示,结合图①,写出完整的证明过程.
(1)、请根据教材提示,结合图①,写出完整的证明过程.
图①
(2)、(结论应用)如图,在四边形 中, , , , 是 的中点,连结 、 .则 的度数为°. (3)、在 中,已知 , , , 为边 的中点, 且与 的平分线交于点 ,则 的长为 .
(3)、在 中,已知 , , , 为边 的中点, 且与 的平分线交于点 ,则 的长为 . 23. 如图,在△ABC中,AB=25,AC=20,BC=15,CN⊥AB , 点P从点A出发,以每秒5个单位的速度沿AB向终点B匀速运动.当点P不与点A、B、N重合时,过点P作PQ⊥AC交AC于点Q , 以PQ、PN为邻边作平行四边形PQMN , 设平行四边形PQMN与△ ABC重叠部分面积为S(平方单位).点P的运动时间为t(秒).
23. 如图,在△ABC中,AB=25,AC=20,BC=15,CN⊥AB , 点P从点A出发,以每秒5个单位的速度沿AB向终点B匀速运动.当点P不与点A、B、N重合时,过点P作PQ⊥AC交AC于点Q , 以PQ、PN为邻边作平行四边形PQMN , 设平行四边形PQMN与△ ABC重叠部分面积为S(平方单位).点P的运动时间为t(秒). (1)、当点P在线段AN上时,tan∠PQM的值是;(2)、用含t的代数式表示线段PN的长度;(3)、当S 时,求t的值;(4)、当点M恰好落在△ABC的角平分线上时,直接写出t的值.24. 已知二次函数 .(1)、当 时,若点 在此二次函数的图象上,求b的值;(2)、若 ,求此二次函数的最大值;(3)、若点 恰好同时落在此二次函数的图象上,求a的值,并直接写出当函数值y随x的增大而增大时x的取值范围;(4)、 的三个顶点的坐标分别为 ,设 的最长边与此二次函数的图象交于点F , 过点F作y轴的垂线,与此函数图象的另一个交点为G , 过点F作x轴的垂线交x轴于点H , 若FG=FH , 直接写出a的值.
(1)、当点P在线段AN上时,tan∠PQM的值是;(2)、用含t的代数式表示线段PN的长度;(3)、当S 时,求t的值;(4)、当点M恰好落在△ABC的角平分线上时,直接写出t的值.24. 已知二次函数 .(1)、当 时,若点 在此二次函数的图象上,求b的值;(2)、若 ,求此二次函数的最大值;(3)、若点 恰好同时落在此二次函数的图象上,求a的值,并直接写出当函数值y随x的增大而增大时x的取值范围;(4)、 的三个顶点的坐标分别为 ,设 的最长边与此二次函数的图象交于点F , 过点F作y轴的垂线,与此函数图象的另一个交点为G , 过点F作x轴的垂线交x轴于点H , 若FG=FH , 直接写出a的值.