吉林省长春市朝阳区2021年中考数学二模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
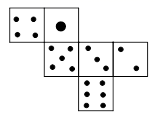
1. 若等式3□(-4)=-1成立,则“□”内的运算符号是( )A、+ B、- C、× D、÷2. 国家统计局1月18日公布,初步核算,2020我国国内生产总值(GDP)首次突破100万亿元,约为1 016 000亿元,其中1 016 000亿用科学记数法表示为( )A、 B、 C、 D、3. 一个正方体的六个面分别标有六个不同的点数,其展开图如下所示,则该正方体可能是( ).
 A、
A、 B、
B、 C、
C、 D、
D、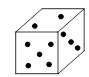 4. 下列运算正确的是( )A、 B、 C、 D、5. 设●、▲、■表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小的顺序排列为 ( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 设●、▲、■表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小的顺序排列为 ( ) A、■、●、▲ B、■、▲、● C、▲、●、■ D、▲、■、●6. 如图,过直径AB延长线上的点C作 的切线,切点为D.若 , ,则sinC的值( )
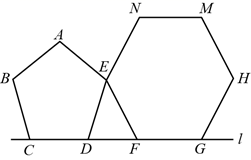
A、■、●、▲ B、■、▲、● C、▲、●、■ D、▲、■、●6. 如图,过直径AB延长线上的点C作 的切线,切点为D.若 , ,则sinC的值( ) A、 B、 C、 D、7. 如图,在 中, , , .按以下步骤作图:①分别以点B和点C为圆心、大于 的长为半径作圆弧,两弧相交于点M和点N;②作直线MN交AC于点D , 则CD的长为( )
A、 B、 C、 D、7. 如图,在 中, , , .按以下步骤作图:①分别以点B和点C为圆心、大于 的长为半径作圆弧,两弧相交于点M和点N;②作直线MN交AC于点D , 则CD的长为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A在函数 的图象上,连结OA , 过点A作AB平行于x轴,点B在点A的右侧,连结OB交该函数图象于点C , 连结AC . 若 ,且 的面积为 ,则k的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A在函数 的图象上,连结OA , 过点A作AB平行于x轴,点B在点A的右侧,连结OB交该函数图象于点C , 连结AC . 若 ,且 的面积为 ,则k的值为( ) A、4 B、6 C、8 D、9
A、4 B、6 C、8 D、9二、解答题
-
9. 计算: .10. 先化简,再求值: ,其中 .11. “航天知识竞赛”活动中,获得“小宇航员”称号的小明得到了A、B、C三枚纪念章.如图,A、B、C三枚纪念章正面上分别印有“嫦娥五号”、“天问一号”和“天宫一号”的图案.三枚纪念章除正面图案不同外,其余均相同,小明将这三枚纪念章背面朝上放在桌面上,然后从中随机选取一枚,记下图案并放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求小明两次抽到图案上至少有一张印有“嫦娥五号”图案的概率.
 12. 为迎接母亲节,某花店老板决定将玫瑰花每枝降价1元促销,降价后,30元可购买玫瑰花的数量是原来可购买玫瑰花数量的1.5倍.求降价后每枝玫瑰花的售价.13. 图①、图②、图③都是 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,在给定的网格中,只用无刻度的直尺,在图①、图②、图③中,按下列要求画图,只保留作图痕迹,不要求写出画法,所画的图形的顶点均在格点上.
12. 为迎接母亲节,某花店老板决定将玫瑰花每枝降价1元促销,降价后,30元可购买玫瑰花的数量是原来可购买玫瑰花数量的1.5倍.求降价后每枝玫瑰花的售价.13. 图①、图②、图③都是 的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,在给定的网格中,只用无刻度的直尺,在图①、图②、图③中,按下列要求画图,只保留作图痕迹,不要求写出画法,所画的图形的顶点均在格点上. (1)、在图①中画一个 ,使其面积为2.(2)、在图②中画一个 ,使其面积为4.(3)、在图③中画一个四边形ABEF , 使其面积为5.14. 某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
(1)、在图①中画一个 ,使其面积为2.(2)、在图②中画一个 ,使其面积为4.(3)、在图③中画一个四边形ABEF , 使其面积为5.14. 某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:次数
成绩
学生
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
169
165
168
169
172
173
169
167
乙
161
174
172
162
163
172
172
176
两名同学的8次跳高成绩数据分析如下表:
名称
成绩
学生
平均数
(单位:cm)
中位数
(单位:cm)
众数
(单位:cm)
方差
(单位:cm2)
甲
a
b
c
5.75
乙
169
172
172
31.25
根据图表信息回答下列问题:
(1)、求a、b、c的值.(2)、这两名同学中,的成绩更为稳定(填“甲”或“乙”).(3)、若预测跳高165cm就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择哪位同学参赛,并说明理由15. 如图,在△ABC中,∠ACB=90°,D是BC边上的一点,分别过点A、B作BD、AD的平行线交于点E,且 AB平分∠EAD. (1)、求证:四边形EADB是菱形;(2)、连接EC,当∠BAC=60°,BC= 时,求△ECB的面积.16. 甲同学骑共享单车保持匀速从家到公园,到达公园后休息了一会,以相同的速度原路骑共享单车返回家中,设甲同学距离家的路程为y(m),运动时间为x(min),y与x之间的函数图象如图所示.
(1)、求证:四边形EADB是菱形;(2)、连接EC,当∠BAC=60°,BC= 时,求△ECB的面积.16. 甲同学骑共享单车保持匀速从家到公园,到达公园后休息了一会,以相同的速度原路骑共享单车返回家中,设甲同学距离家的路程为y(m),运动时间为x(min),y与x之间的函数图象如图所示.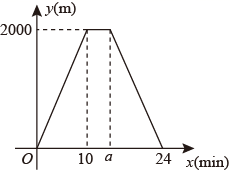 (1)、a= .(2)、在甲同学从公园返回家的过程中,求y与x之间的函数关系式.(3)、在甲同学从家出发的同时,乙同学以100m/min的速度从公园匀速步行去甲同学家学习,当乙同学与甲同学之间的路程为200m时,直接写出甲同学的运动时间.17. 如图
(1)、a= .(2)、在甲同学从公园返回家的过程中,求y与x之间的函数关系式.(3)、在甲同学从家出发的同时,乙同学以100m/min的速度从公园匀速步行去甲同学家学习,当乙同学与甲同学之间的路程为200m时,直接写出甲同学的运动时间.17. 如图 (1)、(问题原型)如图①,四边形ABDE、AGFC都是正方形, ,连结CE、BG . 求证: .(2)、(发现结论)如图②,设图①中的直线CE与直线BG交于点H . 求证: .(3)、(结论应用)将图①中的正方形AGFC绕着点A顺时针旋转角度 ,在整个旋转过程中,当点E、C、G三点在同一条直线上时,若 , ,借助图①,直接写出BG的长.18. 如图,在 中, , , ,D为边AB的中点.动点P从点A出发,以每秒2个单位长度的速度沿折线AC-CB向终点B运动.当点P不与点C重合时,连结PD , 以CP、PD为边作 .设点P的运动时间为t秒.
(1)、(问题原型)如图①,四边形ABDE、AGFC都是正方形, ,连结CE、BG . 求证: .(2)、(发现结论)如图②,设图①中的直线CE与直线BG交于点H . 求证: .(3)、(结论应用)将图①中的正方形AGFC绕着点A顺时针旋转角度 ,在整个旋转过程中,当点E、C、G三点在同一条直线上时,若 , ,借助图①,直接写出BG的长.18. 如图,在 中, , , ,D为边AB的中点.动点P从点A出发,以每秒2个单位长度的速度沿折线AC-CB向终点B运动.当点P不与点C重合时,连结PD , 以CP、PD为边作 .设点P的运动时间为t秒. (1)、C、D两点之间的距离为 .(2)、当点E落在边BC上时,求 的周长.(3)、当点P在边BC上运动时,若四边形CPDE是轴对称图形,求t的值.(4)、设 的对角线的交点为O , 点D关于对角线PE的对称点为 ,连结 ,当 时,直接写出t的值.19. 在平面直角坐标系中,抛物线 (m为常数).(1)、当点 在该抛物线上时,求m的值.(2)、将抛物线在 的部分图象沿y轴翻折得到新图象记为G , 当 时,图象G的函数值y先随x的增大而增大,后随x的增大而减小,求m的取值范围.(3)、当该抛物线在 的部分图象的最高点到 的距离为1时,求m的值.(4)、当 时,过点 作垂直于x轴的直线交该抛物线于点B , 在AB延长上取一点C , 使 ,将线段AB绕点A顺时针旋转 得到线段AE , 以AC、AE为邻边作矩形ACDE , 当该抛物线的顶点在矩形的边上时,直接写出该抛物线在该矩形内部(包含边界)图象所对应的函数的最大值与最小值的差.
(1)、C、D两点之间的距离为 .(2)、当点E落在边BC上时,求 的周长.(3)、当点P在边BC上运动时,若四边形CPDE是轴对称图形,求t的值.(4)、设 的对角线的交点为O , 点D关于对角线PE的对称点为 ,连结 ,当 时,直接写出t的值.19. 在平面直角坐标系中,抛物线 (m为常数).(1)、当点 在该抛物线上时,求m的值.(2)、将抛物线在 的部分图象沿y轴翻折得到新图象记为G , 当 时,图象G的函数值y先随x的增大而增大,后随x的增大而减小,求m的取值范围.(3)、当该抛物线在 的部分图象的最高点到 的距离为1时,求m的值.(4)、当 时,过点 作垂直于x轴的直线交该抛物线于点B , 在AB延长上取一点C , 使 ,将线段AB绕点A顺时针旋转 得到线段AE , 以AC、AE为邻边作矩形ACDE , 当该抛物线的顶点在矩形的边上时,直接写出该抛物线在该矩形内部(包含边界)图象所对应的函数的最大值与最小值的差.三、填空题