黑龙江省齐齐哈尔市建华区2021年中考数学三模试卷

试卷更新日期：2021-07-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果a与﹣2互为相反数，那么a等于（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列图片中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $2 a^{2} + a = 3 a^{3}$ B、 $2 a^{- 1} = \frac{1}{2 a}$ C、 ${(- a)}^{3} \times a^{2} = - a^{6}$ D、 $2 π^{0} = 2$

查看试题解析
4. 下列条件中能判断一个四边形是菱形的是（）

A、对角线互相平分且相等 B、对角线互相垂直且相等 C、对角线互相平分且垂直 D、对角线互相垂直且一条对角线平分一组对角

查看试题解析
5. 一张桌子上摆着若干个碟子，从三个方向上看所得的视图如图所示，则这张桌子上碟子的数量为（）

A、17 B、13 C、12 D、9

查看试题解析
6. 如图， $▱ A B C D$ 中， $∠ B = 60 °$ ， $A B = 4$ ， $B C = 5$ ，P是对角线AC上任一点（点P不与点A、C重合），且 $P E / / B C$ 交AB于E ，且 $P F / / C D$ 交AD于F ，则阴影部分的面积为（）

A、5 B、 $5 \sqrt{3}$ C、10 D、 $10 \sqrt{3}$

查看试题解析
7. 如图，蒙古包可以近似地看作是由圆锥和圆柱组成，若用毛毡搭建一个底面半径为5米，圆柱高3米，圆锥高2米的蒙古包，则需要毛毡的面积为（）

A、 $(30 + 5 \sqrt{29}) π$ 米² B、 $40 π$ 米² C、 $(30 + 5 \sqrt{21}) π$ 米² D、 $55 π$ 米²

查看试题解析
8. 货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x千米/小时，依题意列方程正确的是（）

A、 $\frac{25}{x} = \frac{35}{x - 20}$ B、 $\frac{25}{x - 20} = \frac{35}{x}$ C、 $\frac{25}{x} = \frac{35}{x + 20}$ D、 $\frac{25}{x + 20} = \frac{35}{x}$

查看试题解析
9. 如图，大三角形与小三角形是位似图形．若小三角形一个顶点的坐标为（m ， n），则大三角形中与之对应的顶点坐标为（）

A、（﹣2m ， ﹣2n） B、（2m ， 2n） C、（﹣2n ， ﹣2m） D、（2n ， 2m）

查看试题解析
10. 已知二次函数y＝Ax²＋Bx＋C（A≠0）的图象如图，则下列结论：
①A，B同号；②当x＝1和x＝3时，函数值相等；③4A＋B＝0；④当y＝－2时，x的值只能为0；⑤△﹤0其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. “杂交水稻之父”袁隆平院士一生致力于水稻研究，在2004年获颁世界粮食奖，被视为“亚洲英雄”，上世纪70年代，袁隆平在杂交水稻上取得突破，当时他研究出的杂交水稻相比其它品种年产量提高了20%，意味着每年可多养活7000万人口.7000万人用科学记数法表示为人．

查看试题解析
12. 如图，AD、 $A_{1} D_{1}$ 分别是锐角 $△ A B C$ 和 $△ A_{1} B_{1} C_{1}$ 中 $B C$ 、 $B_{1} C_{1}$ 边上的高，且 $A B = A_{1} B_{1}$ ， $A D = A_{1} D_{1}$ ，请你补充一个适当的条件：，使 $△ A B C ≌ △ A_{1} B_{1} C_{1}$ ．

查看试题解析
13. 一组数据-3，x，-2，3，1，6的中位数是1，则其方差为

查看试题解析
14. 关于x的方程 $\frac{2 x + a}{x - 1} = 1$ 的解是正数，则a的取值范围是．

查看试题解析
15. 有一张直角三角形的纸片ABC ，其中 $∠ A C B = 90 °$ ， $A B = 5$ ， $A C = 4$ ，点D为AC边上的一点，现沿过点D的直线折叠，使直角顶点C恰好落在斜边AB上的点E处，当 $△ A D E$ 是直角三角形时，CD的长为．

查看试题解析
16. 如图，反比例函数 $y = \frac{6}{x}$ 在第一象限的图象上有两点A、B ，它们的横坐标分别为1、3，直线AB与x轴交于点C ，则 $△ O A C$ 的面积为．

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $B C = 1$ ， $C D_{1}$ 为斜边AB上的中线，过点 $D_{1}$ 作 $D_{1} E_{1} ⊥ A C$ 于点 $E_{1}$ ，连接 $B E_{1}$ 交 $C D_{1}$ 于点 $D_{2}$ ；过点 $D_{2}$ 作 $D_{2} E_{2} ⊥ A C$ 于点 $E_{2}$ ，连接 $B E_{2}$ 交 $C D_{1}$ 于点 $D_{3}$ ；…依次作下去，可以得到点 $D_{4}$ 、点 $D_{5}$ 、…点 $D_{n}$ ，分别记 $△ B D_{1} E_{1}$ 、 $△ B D_{2} E_{2}$ 、 $△ B D_{3} E_{3}$ 、 $△ B D_{n} E_{n}$ 的面积为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 、… $S_{n}$ ，则第n个三角形 $△ B D_{n} E_{n}$ 的面积 $S_{n} =$ ．

查看试题解析

三、解答题

18.

(1)、计算： $- 2^{2} - | - \sqrt{12} | - {(\frac{1}{3})}^{- 1} + 2 \tan 60 °$ ；

(2)、分解因式： $4 a^{3} - \frac{a}{4}$

查看试题解析
19. 解方程： $(x + 2) (x - 1) = 2 x (x - 2) + 2$

查看试题解析
20. 学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了右边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：

(1)、该校学生报名总人数有多少人？

(2)、从表中可知选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？

(3)、将两个统计图补充完整．

查看试题解析
21. 如图，点O为矩形ABCD的对角线AC上一点，以OA为半径的⊙O交AD于点E ，交AC于点F ，且 $∠ A C B = ∠ D C E$ ．

(1)、求证：直线CE是⊙O的切线；

(2)、若 $\tan ∠ A C B = \frac{\sqrt{2}}{2}$ ， $B C = 4$ ，求⊙O的半径．

查看试题解析
22. 一队学生从学校出发去劳动基地，行进的路程与时间的函数图象如图所示，队伍走了0.8小时后，队伍中的通讯员按原路加快速度返回学校取材料．通讯员经过一段时间回到学校，取到材料后立即按返校时加快的速度追赶队伍，并比学生队伍早18分钟到达基地．如图，线段OD表示学生队伍距学校的路程y（千米）与时间x（小时）之间的函数关系，折线OABC表示通讯员距学校的路程y（千米）与时间x（小时）之间的函数关系，请你根据图象信息，解答下列问题：

(1)、图中的 $m =$ 千米， $a =$ 小时，点B的坐标为；

(2)、求通讯员距学校的路程y（千米）与时间x（小时）之间的函数关系式；

(3)、若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系，请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围．
答：．

查看试题解析
23. 综合与实践

(1)、动手、发现：数学活动课上，小明进行了下列操作：
“如图①，矩形纸片ABCD中，BD为对角线，将 $△ B C D$ 沿BD折叠，使点C落在点E处，BE交AD于点F”则线段 $B F =$ ， $△ A B F ≌ △$ ；

(2)、问题解决：在图①中，若 $A B = 6$ ， $B C = 8$ ，请你求出：线段AF的长及 $\tan ∠ A B F$ 的值；

(3)、再动手、延伸：小明在（2）的条件下，找到DE上的点G及BD上的点H ，将 $△ G D H$ 沿GH折叠，使点D落在点A处，GH交AD于点K（如图②），则 $G H =$ ， $\sin ∠ G A H =$ ．

查看试题解析
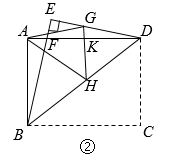24. 综合与探究
如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c (a > 0)$ 的图象的顶点为D点与x轴交于A、B两点，与y轴交于C点，A点在原点的左侧，B点的坐标为 $(3 ， 0)$ ， $O B = O C$ ， $\tan ∠ A C O = \frac{1}{3}$ ．

(1)、求这个二次函数的解析式；

(2)、若点 $G (2 ， y)$ 是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时， $△ A P G$ 的面积最大？求出此时P点的坐标和 $△ A P G$ 的最大面积；

(3)、经过C、D两点的直线，与x轴交于点E ．
①请你直接写出 $△ B C E$ 的面积；

②在该抛物线上是否存在这样的点F ，使以点A、点C、点E、点F为顶点的四边形为平行四边形？若存在，请直接写出点 F的坐标；若不存在，请说明理由．

查看试题解析