黑龙江省哈尔滨市道外区2021年中考数学一模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 16的算术平方根是( )A、4 B、8 C、±4 D、22. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 下列图形中,轴对称图形有( )
 A、0个 B、1个 C、2个 D、3个4. 如图中几何体的俯视图是( )
A、0个 B、1个 C、2个 D、3个4. 如图中几何体的俯视图是( ) A、
A、 B、
B、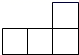 C、
C、 D、
D、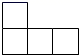 5. 方程 = 的解为( )A、1 B、﹣1 C、4 D、6. 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、y=(x-1)2+2 B、y=(x+1)2+2 C、y=(x-1)2-2 D、y=(x+1)2-27. 若双曲线y= 的图象在第一、三象限,则k的取值范围为( )A、k>0 B、k<0 C、k>1 D、k<18. 如图,P为⊙O外一点,PA、PB是⊙O 的切线,A , B为切点,点C为AB左侧⊙O上一点,若∠P=50°,则∠ACB的度数为( )
5. 方程 = 的解为( )A、1 B、﹣1 C、4 D、6. 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、y=(x-1)2+2 B、y=(x+1)2+2 C、y=(x-1)2-2 D、y=(x+1)2-27. 若双曲线y= 的图象在第一、三象限,则k的取值范围为( )A、k>0 B、k<0 C、k>1 D、k<18. 如图,P为⊙O外一点,PA、PB是⊙O 的切线,A , B为切点,点C为AB左侧⊙O上一点,若∠P=50°,则∠ACB的度数为( ) A、50° B、55° C、60° D、65°9. 如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD , 若 ,则∠ABE的度数为( )
A、50° B、55° C、60° D、65°9. 如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD , 若 ,则∠ABE的度数为( ) A、25° B、30° C、35° D、40°10. 如图,四边形ABCD是平行四边形,点E在CD边上,则下列结论错误的是( )
A、25° B、30° C、35° D、40°10. 如图,四边形ABCD是平行四边形,点E在CD边上,则下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 全国第十三届人民代表大会政府工作报告提出,在未来5年力争改造城镇老旧小区53000个,把53000这个数用科学记数法表示为 .12. 在函数y= 中,自变量x的取值范围是 .13. 计算 ﹣ = .14. 把多项式 分解因式的结果是.15. 不等式组 的解集是。16. 二次函数y=x2﹣2x+m的最小值为2,则m的值为 .17. 一个扇形的半径为3cm,面积为 ,则此扇形的圆心角为.18. 在一个不透明的袋子中有红、绿各两个小球,它们只有颜色上的区别.从袋子中随机摸出一个小球记下颜色后不放回.再随机摸一个.则两次都摸到红球概率为 .19. △ABC中,∠ACB=90°,CD是高,∠BEC=2∠ABC , 若AB=10,DE=1,则AD的长为 .20. 如图,四边形ABCD中,AB=AC=AD , 且∠ABD=2∠BDC , 若CE=2,DE=5,则BE的长为 .

三、解答题
-
21. 先化简,再求代数式(1﹣ )÷(x+1﹣ )的值,其中x=tan60°+4sin30°.22. 如图,在6×8的正方形网格中,每个小正方形的边长都为1,点A、B均在小正方形的顶点上.

⑴画一个以BC为底的等腰△ABC , 使点C在小正方形的顶点上;
⑵再在△ABC内画一个以AC为底的等腰△ACD , 使D在小正方形的顶点上,连接BD
23. 全国政协十三届四次会议共收到委员提案约6000件,先从中提取部分委员提案进行调查.根据收集数据,绘制两幅不完整的统计图.请你根据图中提供的信息 (1)、在这次调查中,一共抽多少件提案;(2)、通过计算,补全条形统计图;(3)、通过计算估计本次会议关于“政治文化建设”方面的提案有多少件.24. 如图,△ABC中,AB=AC , M为AD中点,过点A作AE∥BC交BM延长线于点E , 连接CE .
(1)、在这次调查中,一共抽多少件提案;(2)、通过计算,补全条形统计图;(3)、通过计算估计本次会议关于“政治文化建设”方面的提案有多少件.24. 如图,△ABC中,AB=AC , M为AD中点,过点A作AE∥BC交BM延长线于点E , 连接CE . (1)、求证:四边形ADCE为矩形;(2)、连接DE交AC于点G , 连接MG , 在不添加辅助线的条件下请直接写出面积等于△ABM面积一半的所有三角形.25. 某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.(1)、该商场购进这种彩灯的实际进价为多少元?(2)、该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?26. 如图,AB为⊙O的直径,弦CD交AB于点E , 且DE=OE
(1)、求证:四边形ADCE为矩形;(2)、连接DE交AC于点G , 连接MG , 在不添加辅助线的条件下请直接写出面积等于△ABM面积一半的所有三角形.25. 某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.(1)、该商场购进这种彩灯的实际进价为多少元?(2)、该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?26. 如图,AB为⊙O的直径,弦CD交AB于点E , 且DE=OE (1)、求证:∠BAC=3∠ACD;(2)、点F在弧BD上,且∠CDF= ∠AEC , 连接CF交AB于点G,求证:CF=CD;(3)、在(2)的条件下,若OG=4,FG=11,求⊙O的半径.27. 如图,抛物线y=a(x+2)(x﹣5)(a<0)交x轴于A、B两点(A左B右),且5OA=2OC .
(1)、求证:∠BAC=3∠ACD;(2)、点F在弧BD上,且∠CDF= ∠AEC , 连接CF交AB于点G,求证:CF=CD;(3)、在(2)的条件下,若OG=4,FG=11,求⊙O的半径.27. 如图,抛物线y=a(x+2)(x﹣5)(a<0)交x轴于A、B两点(A左B右),且5OA=2OC . (1)、求抛物线的解析式;(2)、P为第一象限抛物线上一点,连接PA交y轴于点D , 设点P的横坐标为m , △PCD的面积为S,求S与m的函数关系式;(3)、在(2)的条件下,连接BC交PA于点E , 交BC于点F , 若PE=PF , 求P点坐标.
(1)、求抛物线的解析式;(2)、P为第一象限抛物线上一点,连接PA交y轴于点D , 设点P的横坐标为m , △PCD的面积为S,求S与m的函数关系式;(3)、在(2)的条件下,连接BC交PA于点E , 交BC于点F , 若PE=PF , 求P点坐标.