黑龙江省哈尔滨市道外区2021年中考数学三模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 下列各数中,比-3小的数是( ).A、-3 B、2 C、0 D、-42. 下列计算中,结果正确的是( ).A、 B、 C、 D、3. 下列所给的交通标志中,是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 4. 如图所示,其俯视图是( ).
4. 如图所示,其俯视图是( ). A、
A、 B、
B、 C、
C、 D、
D、 5. 将抛物线y=2x2+1向左平移1个单位,再向下平移3个单位后所得到的抛物线为( )A、 B、 C、 D、6. 方程 = 的解为( )A、x=3 B、x=4 C、x=5 D、x=﹣57. 若正比例函数 与反比例函数 图象的一个交点的横坐标为-1,则 的值为( ).A、1 B、-1 C、2 D、-28. 如图, 、 为 的切线, 、 为切点,点 为弧 上一点,过点 作 的切线分别交 、 于 、 ,若 ,则 的周长等于( ).
5. 将抛物线y=2x2+1向左平移1个单位,再向下平移3个单位后所得到的抛物线为( )A、 B、 C、 D、6. 方程 = 的解为( )A、x=3 B、x=4 C、x=5 D、x=﹣57. 若正比例函数 与反比例函数 图象的一个交点的横坐标为-1,则 的值为( ).A、1 B、-1 C、2 D、-28. 如图, 、 为 的切线, 、 为切点,点 为弧 上一点,过点 作 的切线分别交 、 于 、 ,若 ,则 的周长等于( ).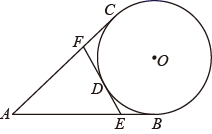 A、6 B、12 C、9 D、189. 如图,将矩形纸片 沿着 折叠,使 、 分别落在 、 处,若 ,则 的度数为( ).
A、6 B、12 C、9 D、189. 如图,将矩形纸片 沿着 折叠,使 、 分别落在 、 处,若 ,则 的度数为( ).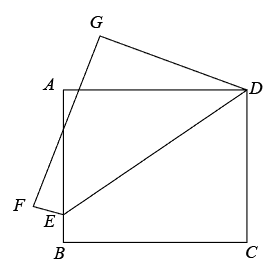 A、 B、 C、 D、10. 如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).
A、 B、 C、 D、10. 如图,四边形 中, 为对角线 上一点,过点 作 ,交 于点 ,过点 作 ,交 于点 ,则下列所给的结论中,不一定正确的是( ).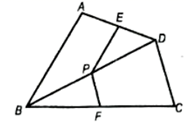 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
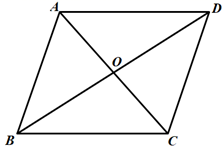
11. 将数字 用科学记数法表示为 .12. 计算: .13. 函数 的自变量 的取值范围是 .14. 把多项式 分解因式的结果是 .15. 不等式组的 解集是 .16. 二次函数 的顶点坐标为 .17. 某扇形的圆心角为 ,面积为 ,该扇形的弧长为 .18. 在一个不透明的袋子中装有6个除颜色外形状大小完全相同的球,其中有2个红球、2个蓝球、2个白球,现从中摸出两个球,则摸出两个球都是红球的概率是 .19. 为 的直径, 为半圆弧 的中点,点 在 上,且 ,若 ,则 的长为 .20. 中, , 、 相交于点O , 且 ,若 ,则 的长为 .
三、解答题
-
21. 先化简,再求值: ,其中a=2sin60°-3tan45°22. 如图,在 的方格纸中,每个小正方形的边长为1,点 、 均在小正方形的顶点上,请按要求画出图形并计算.
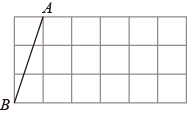 (1)、画出 ,使得 ,点 在小正方形的顶点上,且 的面积为7.5;(2)、画出点 ,点 在小正方形的顶点上,且 ,并直接写出 边的长.23. 为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,毛毛对该班同学参加锻炼的情况进行了统计(每人只能选其中一项),并绘制了如图两个统计图,请根据图中提供的信息解答下列问题:
(1)、画出 ,使得 ,点 在小正方形的顶点上,且 的面积为7.5;(2)、画出点 ,点 在小正方形的顶点上,且 ,并直接写出 边的长.23. 为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,毛毛对该班同学参加锻炼的情况进行了统计(每人只能选其中一项),并绘制了如图两个统计图,请根据图中提供的信息解答下列问题: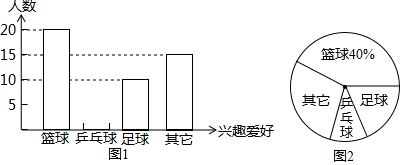 (1)、毛毛这次一共调查了多少名学生?(2)、补全条形统计图,并求出扇形统计图中“足球”所在扇形的圆心角度数;(3)、若该校有1800名学生,请估计该校喜欢乒乓球的学生约有多少人.24. 如图,在 中.点 在 边上,点 在 边上,且 ,连接 、 相交于点 ,连接 、 相交于点.
(1)、毛毛这次一共调查了多少名学生?(2)、补全条形统计图,并求出扇形统计图中“足球”所在扇形的圆心角度数;(3)、若该校有1800名学生,请估计该校喜欢乒乓球的学生约有多少人.24. 如图,在 中.点 在 边上,点 在 边上,且 ,连接 、 相交于点 ,连接 、 相交于点.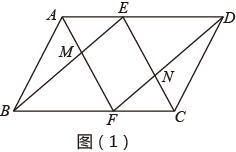
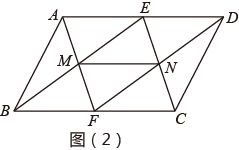 (1)、如图1,求证:四边形 为平行四边形;(2)、如图2,连接 ,若 是 的中点,在不添加任何辅助线的情况下,请直接写出图2中以 为边的所有平行四边形.25. 南京市某花卉种植基地欲购进甲、乙两种兰花进行培育,每株甲种兰花的成本比每株乙种兰花的成本多100元,且用1200元购进的甲种兰花与用900元购进的乙种兰花数量相同.(1)、求甲、乙两种兰花每株成本分别为多少元?(2)、该种植基地决定在成本不超过30000元的前提下培育甲、乙两种兰花,若培育乙种兰花的株数比甲种兰花的3倍还多10株,求最多购进甲种兰花多少株?26. 如图, 为 的直径, 为 延长线上一点,点 在 上,连接 交 于点 , .
(1)、如图1,求证:四边形 为平行四边形;(2)、如图2,连接 ,若 是 的中点,在不添加任何辅助线的情况下,请直接写出图2中以 为边的所有平行四边形.25. 南京市某花卉种植基地欲购进甲、乙两种兰花进行培育,每株甲种兰花的成本比每株乙种兰花的成本多100元,且用1200元购进的甲种兰花与用900元购进的乙种兰花数量相同.(1)、求甲、乙两种兰花每株成本分别为多少元?(2)、该种植基地决定在成本不超过30000元的前提下培育甲、乙两种兰花,若培育乙种兰花的株数比甲种兰花的3倍还多10株,求最多购进甲种兰花多少株?26. 如图, 为 的直径, 为 延长线上一点,点 在 上,连接 交 于点 , .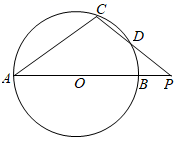 (1)、求证: ;(2)、过点 作弦 ,垂足为 , 交 于点 ,求证: ;
(1)、求证: ;(2)、过点 作弦 ,垂足为 , 交 于点 ,求证: ;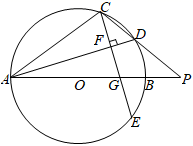 (3)、在(2)的条件下,过点 作 ,垂足为 ,若 , ,求 的半径.
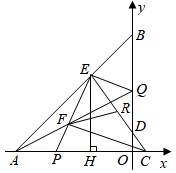
(3)、在(2)的条件下,过点 作 ,垂足为 ,若 , ,求 的半径.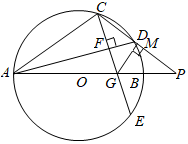 27. 如图,直线 交 轴于点 ,交 轴于点 ,直线 交 轴于点 ,交 轴于点 ,交直线 于点 ,过点 作 轴,垂足为 ,且 .
27. 如图,直线 交 轴于点 ,交 轴于点 ,直线 交 轴于点 ,交 轴于点 ,交直线 于点 ,过点 作 轴,垂足为 ,且 .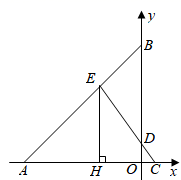 (1)、求b的值;(2)、 为线段 上一点,过点 作 的垂线,交 轴于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 的函数关系式;
(1)、求b的值;(2)、 为线段 上一点,过点 作 的垂线,交 轴于点 ,设点 的横坐标为 ,线段 的长为 ,求 与 的函数关系式;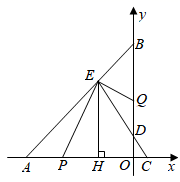 (3)、在(2)的条件下,连接 交 于点 ,且 ,点 在线段 上,若 ,求点 的坐标.
(3)、在(2)的条件下,连接 交 于点 ,且 ,点 在线段 上,若 ,求点 的坐标.