河北省张家口市桥东区2021年中考数学二模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 下列由实线组成的图形中,为半圆的是( )A、
 B、
B、 C、
C、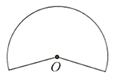 D、
D、 2. 下列各数中比 小的数是( )A、0 B、 C、1 D、-23. 如图是东西流向且两岸 , 互相平行的一段河道,在河岸 有一棵小树 ,在河岸 的琪琪观测到小树 在他的北偏西 方向上,则琪琪的位置可能是( )
2. 下列各数中比 小的数是( )A、0 B、 C、1 D、-23. 如图是东西流向且两岸 , 互相平行的一段河道,在河岸 有一棵小树 ,在河岸 的琪琪观测到小树 在他的北偏西 方向上,则琪琪的位置可能是( ) A、 B、 C、 D、4. 小强把一个六位数表示成了“ ”,则用科学记数法表示这个六位数应为( )A、 B、 C、 D、5. 如图,观察由6个大小相同的小正方体组成的几何体,它的主视图、左视图、俯视图对应的序号依次是( )
A、 B、 C、 D、4. 小强把一个六位数表示成了“ ”,则用科学记数法表示这个六位数应为( )A、 B、 C、 D、5. 如图,观察由6个大小相同的小正方体组成的几何体,它的主视图、左视图、俯视图对应的序号依次是( )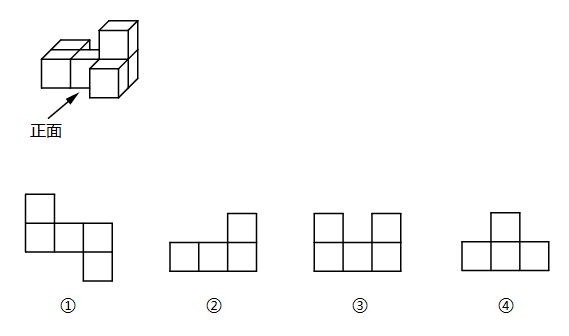 A、②,④,① B、①,②,③ C、②,④,③ D、④,②,③6. 关于 进行的变形或运算:
A、②,④,① B、①,②,③ C、②,④,③ D、④,②,③6. 关于 进行的变形或运算:① ;② ;③ ;④ .其中错误的是( )
A、①② B、③④ C、①③ D、②④7. 当 时,计算 的值为( )A、2 B、-2 C、 D、8. 刘老师从某校2000名学生每天体育锻炼时长的问卷中,随机抽取部分学生的答卷,将这部分学生的锻炼时长作为一个样本进行研究,并将结果绘制成如图的条形统计图,其中一部分被墨迹遮盖,已知每天锻炼时长为1小时的学生人数占样本总人数的36%,则下列说法正确的是( )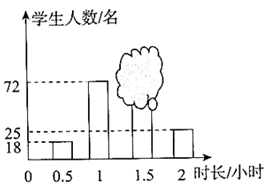 A、样本容量小于200 B、2000名学生是总体 C、锻炼时长为1.5小时是这个样本的众数 D、该校锻炼用时为2小时的学生约有200名9. 如图,在平面直角坐标系中,矩形 与矩形 是以点 为位似中心的位似图形,点 的坐标为 ,若 ,则 的长是( )
A、样本容量小于200 B、2000名学生是总体 C、锻炼时长为1.5小时是这个样本的众数 D、该校锻炼用时为2小时的学生约有200名9. 如图,在平面直角坐标系中,矩形 与矩形 是以点 为位似中心的位似图形,点 的坐标为 ,若 ,则 的长是( ) A、3 B、4 C、4.5 D、610. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.
A、3 B、4 C、4.5 D、610. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.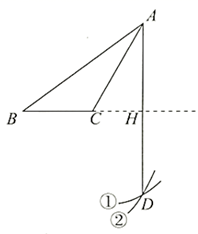
步骤1:以 为圆心, 长为半径画弧①;
步骤2:以 为圆心, 长为半径画弧②,交弧①于点 ;
步骤3:连接 ,交 的延长线于点 .
则下列说法错误的是( )
A、 是 中 边上的高 B、 C、 平分 D、作图依据是:①两点确定一条直线;②到线段两端点距离相等的点在线段的垂直平分线上11. 若 比 与 的积小1,则关于 的值,下列说法正确的是( )A、不存在这样 的值 B、有两个相等的 的值 C、有两个不相等的 的值 D、无法确定12. 如图,两根木条钉成一个角形框架 ,且 , ,将一根橡皮筋两端固定在点 , 处,拉展成线段 ,在平面内,拉动橡皮筋上的一点 ,当四边形 是菱形时,橡皮筋再次被拉长了( )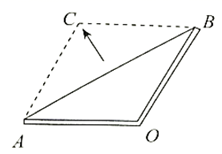 A、 B、 C、 D、13. 若 ( , , 都为正整数),则 的最小值为( )A、3 B、4 C、6 D、914. 阅读图中的材料,解答下面的问题:
A、 B、 C、 D、13. 若 ( , , 都为正整数),则 的最小值为( )A、3 B、4 C、6 D、914. 阅读图中的材料,解答下面的问题:已知 是一个正十二边形的外接圆,该正十二边形的半径为1,如果用它的面积来近似估计 的面积,则 的面积约是( )

我国魏晋时期著名数学家刘徽在“刻圆术”中提出:当正多边形的边数无限增加时,这个正多边形面积可无限接近它的外接圆面积,因此可以用正多边形的面积来进似估计这个圆的面积.
A、3 B、3.1 C、3.14 D、15. 如图,在平面直角坐标系中,直线 ,直线 与 轴分别交于点 , ,且 与 交于点 ,若点 在 的内部(不包括边界),则m的值可能为( ) A、 B、 C、 D、016. 如图,点 为 的内心, , ,点 , 分别为 , 上的点,且 .
A、 B、 C、 D、016. 如图,点 为 的内心, , ,点 , 分别为 , 上的点,且 .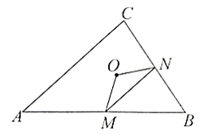
甲、乙、丙三人有如下判断:
甲: ;乙:四边形 的面积是定值;丙:当 时, 的周长取得最小值.则下列说法正确的是( )
A、只有甲正确 B、只有丙错误 C、乙、丙都正确 D、甲、乙、丙都错误二、填空题
-
17. 计算: .18. 将一副三角尺 和 按图所示位置摆放,若 ,则 .
 19. 如图,在平面直角坐标系中, 的顶点分别为 , , ,曲线 ( ).
19. 如图,在平面直角坐标系中, 的顶点分别为 , , ,曲线 ( ).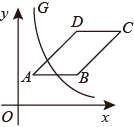 (1)、点 的坐标为 .(2)、当曲线 经过 的对角线的交点时, 的值为 .(3)、若 刚好将 边上及其内部的“整点”(横、纵坐标都为整数的点)分成数量相等的两部分,则 的取值范围是 .
(1)、点 的坐标为 .(2)、当曲线 经过 的对角线的交点时, 的值为 .(3)、若 刚好将 边上及其内部的“整点”(横、纵坐标都为整数的点)分成数量相等的两部分,则 的取值范围是 .三、解答题
-
20. 对有序数对 规定运算: .例如, .(1)、求 的结果;(2)、若 ,求 的值.21. 甲、乙两人各持一张分别写有整式 、 的卡片.已知整式 ,下面是甲、乙二人的对话:
甲:我的卡片上写着整式 ,加上整式 后得到最简整式 ;
乙:我用最简整式 加上整式 后得到整式 .
根据以上信息,解决下列问题:
(1)、求整式D和B;(2)、请判断整式 和整式 的大小,并说明理由.22. 某文具店对A , B , C , D , E五种笔记本的售价进行调整,并将调整前后的笔记本售价(均为整数)绘制成如图所示的不完整折线图,已知调整前后的五种笔记本的平均售价相同,且这五种笔记本的平均售价为7元.
品种
A
B
C
D
E
购买数量/本
2
3
3
1
1
(1)、补全折线图;(2)、价格调整后,小亮某次购买笔记本的情况如表所示,直接写出这些笔记本价格的中位数;请判断这些笔记本的平均售价是否与五种笔记本的平均售价相同,并说明理由;(3)、调价后,文具店将五种笔记本各一本摆在柜台上,小丽随机从中拿出一本.①选中调价后的售价不低于调价前售价的笔记本的概率为 ▲ .
②若小丽拿出的是一本C种笔记本,她还要从余下的四本中随机拿出两本,用树状图法或列表法求她选中B种笔记本的概率.
23. 某车间在3月份和4月份加工了A , B两种型号的零件,规定每名工人当月只加工一种型号的零件,且每名工人每个月加工A型(或B型)零件的数量相同,该车间加工A , B两种型号零件的人数与加工总量的情况如下表:时间
3月
4月
型号
A
B
A
B
人数/人
25
20
20
10
加工个数
5400
4200
(1)、求每名工人每个月加工A型或B型零件的数量各是多少个.(2)、5月份该车间将加工两种零件的总人数增加到80人,且每人的工作效率不变,设加工A型零件的工人有 人,5月份加工总量为 个,求 与 的函数关系式.(3)、在(2)的条件下,若加工A型零件的数量不得超过B型零件的5倍,且不少于4200个,则5月份该车间加工零件的数量将控制在什么范围之内?24. 如图,在等边 中, ,将 绕点 逆时针旋转 ( )到线段 的位置,连接 , 与 交于点 ,点 为 上一点,且 ,连接 . (1)、若 ,则 ;(2)、当 时,请判断 与 是否全等,并求此时 的长度;(3)、在 绕点 逆时针旋转的过程中, 的长是否存在最小值?若存在,则直接写出这个最小值;若不存在,请说明理由.25. 如图,抛物线 ( 为常数)与 轴和 轴的正半轴分别交于点 和 ,直线 , 交 轴于点 ,交 于点 , ( 在 的左侧).
(1)、若 ,则 ;(2)、当 时,请判断 与 是否全等,并求此时 的长度;(3)、在 绕点 逆时针旋转的过程中, 的长是否存在最小值?若存在,则直接写出这个最小值;若不存在,请说明理由.25. 如图,抛物线 ( 为常数)与 轴和 轴的正半轴分别交于点 和 ,直线 , 交 轴于点 ,交 于点 , ( 在 的左侧).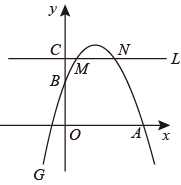 (1)、当 时,
(1)、当 时,①直接写出抛物线 的对称轴和顶点坐标,并求 的长;
②当 时,求 的最大值和最小值的差.
(2)、是否存在 ,使 ?若存在,求出 的值;若不存在,说明理由;(3)、当 时,抛物线 的最高点到 的距离为1,请直接写出此时 的值.26. 如图,矩形 中, , ( ),点 是 上一点(不与点 , 重合),连接 , 与 关于 对称, 是过点 , , 的半圆 的切线,且 交射线 于点 . (1)、当 时,半圆 与 所围成的封闭图形的面积为;(2)、当 在矩形 内部时,
(1)、当 时,半圆 与 所围成的封闭图形的面积为;(2)、当 在矩形 内部时,①判断 与 是否相等,并说明理由;
②若 ,求 的长;
(3)、当 时,若点 落在矩形 的对称轴上,求 的值及此时半圆 落在矩形 内部的弧长.