河北省廊坊市安次区2021年中考数学二模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 下列各数中比-2小的数是( )A、-3 B、-1 C、0 D、22. 计算 的结果是( )A、 B、 C、 D、3. 实数a , b在数轴上的位置如图所示,下列结论中正确的是( )
 A、 B、 C、 D、4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、
A、 B、 C、 D、4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、 B、
B、 C、
C、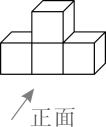 D、
D、 5. 一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是( )A、 B、 C、 D、6. 下列各式从左到右的变形中,错误的是( )A、 B、 C、 D、7. 一个整数81555…0用科学记数法表示为 ;则原数中“0”的个数为( )A、4 B、6 C、7 D、108. 下列各选项中因式分解正确的是( )A、 B、 C、 D、9. 如图,从点 观测建筑物 的仰角是( )
5. 一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是( )A、 B、 C、 D、6. 下列各式从左到右的变形中,错误的是( )A、 B、 C、 D、7. 一个整数81555…0用科学记数法表示为 ;则原数中“0”的个数为( )A、4 B、6 C、7 D、108. 下列各选项中因式分解正确的是( )A、 B、 C、 D、9. 如图,从点 观测建筑物 的仰角是( ) A、 B、 C、 D、10. 如图 是 切线,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( )
A、 B、 C、 D、10. 如图 是 切线,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( ) A、 B、 C、 D、11. 已知在同一直角坐标系中二次函数 和反比例函数 的图象如图所示,则一次函数 的图象可能是( )
A、 B、 C、 D、11. 已知在同一直角坐标系中二次函数 和反比例函数 的图象如图所示,则一次函数 的图象可能是( )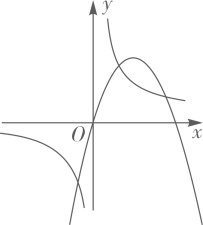 A、
A、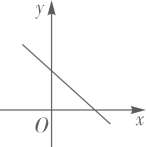 B、
B、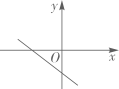 C、
C、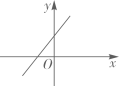 D、
D、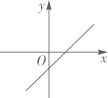 12. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个13. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )
12. 直线 不经过第二象限,则关于 的方程 实数解的个数是( ).A、0个 B、1个 C、2个 D、1个或2个13. 如图,点E是 的边 上的一点,且 ,连接 并延长交 的延长线于点F,若 ,则 的周长为( )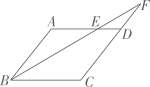 A、21 B、28 C、34 D、4214. 根据尺规作图的痕迹,可以判定点O为 的内心的是( )A、
A、21 B、28 C、34 D、4214. 根据尺规作图的痕迹,可以判定点O为 的内心的是( )A、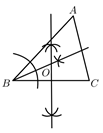 B、
B、 C、
C、 D、
D、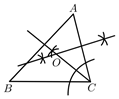 15. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x(元)所在的范围为( )A、 B、 C、 D、16. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
15. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x(元)所在的范围为( )A、 B、 C、 D、16. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
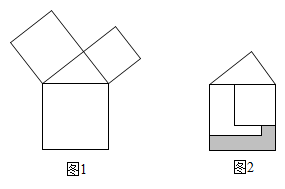 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和二、填空题
-
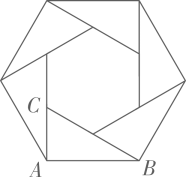
17. 计算: = .18. 如图所示的六边形花环是用六个全等的直角三角形拼成的,则 等于度.
 19. 如图,在平面直角坐标系xOy中,等边三角形△AOB的顶点A在第一象限,点B(3,0),双曲线 (k>0,x>0)把△AOB分成两部分.
19. 如图,在平面直角坐标系xOy中,等边三角形△AOB的顶点A在第一象限,点B(3,0),双曲线 (k>0,x>0)把△AOB分成两部分.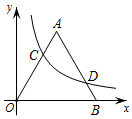 (1)、双曲线与边OA , AB分别交于C , D两点,若OC=2,则k= , 点D的横坐标为;(2)、横纵坐标都为整数的点称为整点,若双曲线 (k>0,x>0)把△AOB分成的两部分内的整点个数相等(不含边界),则k的取值范围为 .
(1)、双曲线与边OA , AB分别交于C , D两点,若OC=2,则k= , 点D的横坐标为;(2)、横纵坐标都为整数的点称为整点,若双曲线 (k>0,x>0)把△AOB分成的两部分内的整点个数相等(不含边界),则k的取值范围为 .三、解答题
-
20. 老师在黑板上出示了下面的5个未计算完的有理数.
, , , ,
(1)、求这5个数的和,并直接写出这5个数的中位数.(2)、在这5个数中,最大的数是m , 最小的数是n . 求 的值.21. 如图,A , B两张卡片除内容外完全相同,现将两张卡片扣在桌面上,随机抽取一张,将抽中卡片上的整式各项改变符号后与未抽中卡片上的整式相加,并将结果化简得到整式C . (1)、若抽中的卡片是B .
(1)、若抽中的卡片是B .①求整式C;
②当x= ﹣1时,求整式C的值.
(2)、若无论x取何值,整式C的值都是非负数,请通过计算,判断抽到的是哪张卡片?22. 一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).(1)、小红摸出标有数3的小球的概率是 .(2)、请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.(3)、求点P(x,y)在函数y=﹣x+5图象上的概率.23. 如图1,在正方形ABCD中, ,点O、E在边CD上,且 , ,以点O为圆心,OE为半径在其左侧作半圆O , 分别交AD于点G , 交CD延长线于点F .
 (1)、 .(2)、如图2,将半圆O绕点E逆时针旋转 ,点O的对应点为 ,点F对应点为 ,当半圆 交BC于P、R两点时,若弧PR的长为 ,求此时半圆 与正方形ABCD重叠部分的面积.(3)、当半圆 与正方形ABCD相切时,设切点为N , 直接写出 的值.24. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.
(1)、 .(2)、如图2,将半圆O绕点E逆时针旋转 ,点O的对应点为 ,点F对应点为 ,当半圆 交BC于P、R两点时,若弧PR的长为 ,求此时半圆 与正方形ABCD重叠部分的面积.(3)、当半圆 与正方形ABCD相切时,设切点为N , 直接写出 的值.24. 某种机器工作前先将空油箱加满,然后停止加油立即开始工作,当停止工作时,油箱中油量为 .在整个过程中,油箱里的油量y(单位:L)与时间x(单位: )之间的关系如图所示.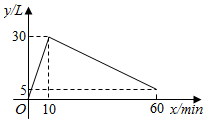 (1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.25. 如图,在平面直角坐标系中,过点 的抛物线 .分别交 轴于 , 两点(点 在点 的左侧),交 轴于点 .
(1)、机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L.(2)、求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.(3)、直接写出油箱中油量为油箱容积的一半时x的值.25. 如图,在平面直角坐标系中,过点 的抛物线 .分别交 轴于 , 两点(点 在点 的左侧),交 轴于点 . (1)、求抛物线的函数表达式.(2)、若点 是抛物线对称轴上一点,当 取得最小值时,求点 的坐标.(3)、当 , 两点满足: , ,且 时,若符合条件的 点的个数有2个,直接写出 的取值范围.26. 如图,在 中, , , ,M是BC的中点,点P从点M出发沿MB以每秒1个单位长度的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长度的速度在射线MC上匀速运动,在点P , Q的运动过程中,以PQ为边作等边 ,使它和 在射线BC的同侧,点P , Q同时出发,点P返回到点M时终止运动,点Q也随之停止,设点P , Q运动时间是t秒 .
(1)、求抛物线的函数表达式.(2)、若点 是抛物线对称轴上一点,当 取得最小值时,求点 的坐标.(3)、当 , 两点满足: , ,且 时,若符合条件的 点的个数有2个,直接写出 的取值范围.26. 如图,在 中, , , ,M是BC的中点,点P从点M出发沿MB以每秒1个单位长度的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长度的速度在射线MC上匀速运动,在点P , Q的运动过程中,以PQ为边作等边 ,使它和 在射线BC的同侧,点P , Q同时出发,点P返回到点M时终止运动,点Q也随之停止,设点P , Q运动时间是t秒 . (1)、当 秒时,点E刚好落在边AD上.(2)、当 时,求 与 重叠部分面积.(3)、随着时间t的变化, 的外心是否一直在 内部?如果在,请说明理由;如果不在,直接写出 的外心在 外部时t的取值范围.
(1)、当 秒时,点E刚好落在边AD上.(2)、当 时,求 与 重叠部分面积.(3)、随着时间t的变化, 的外心是否一直在 内部?如果在,请说明理由;如果不在,直接写出 的外心在 外部时t的取值范围.