广东省惠州市惠城区2021年中考数学二模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. ﹣ 的绝对值是( )A、﹣20 B、20 C、 D、﹣2. 随着科技不断发展,芯片的集成度越来越高,我国企业中芯国际已经实现14纳米量产,14纳米 毫米,0.000014用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 从1,3,5,7中任取两个数,则下列事件中是随机事件的是( )A、两个数的和为奇数 B、两个数的和为偶数 C、两个数的积为偶数 D、两个数的积为3的倍数6. 在“美丽乡村”评选活动中,某乡镇7个村的得分如下:10,7,6,9,8,9,5,这组数据的中位数和众数分别是( )A、7,9 B、9,9 C、8,9 D、9,87. 如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P , 交CD于点Q , 分别以P、Q为圆心,大于 PQ为半径画弧交于点M , 连接DM并延长,交BC于点E , 连接AE , 恰好有AE⊥BC , 则AE的长为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 从1,3,5,7中任取两个数,则下列事件中是随机事件的是( )A、两个数的和为奇数 B、两个数的和为偶数 C、两个数的积为偶数 D、两个数的积为3的倍数6. 在“美丽乡村”评选活动中,某乡镇7个村的得分如下:10,7,6,9,8,9,5,这组数据的中位数和众数分别是( )A、7,9 B、9,9 C、8,9 D、9,87. 如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P , 交CD于点Q , 分别以P、Q为圆心,大于 PQ为半径画弧交于点M , 连接DM并延长,交BC于点E , 连接AE , 恰好有AE⊥BC , 则AE的长为( ) A、3 B、4 C、5 D、8. 如图,已知 ,那么下列结论正确的是( )
A、3 B、4 C、5 D、8. 如图,已知 ,那么下列结论正确的是( )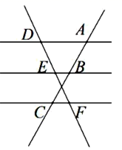 A、 B、 C、 D、9. 如图,正方形 的边 , 和 都是以 为半径的圆弧,阴影两部分的面积分别记为 和 ,则 - 等于( )
A、 B、 C、 D、9. 如图,正方形 的边 , 和 都是以 为半径的圆弧,阴影两部分的面积分别记为 和 ,则 - 等于( ) A、 B、 C、 D、10. 如图,正方形 的边 ,对角线 和 交于点 , 是边 上靠近点 的三等分点,连接 , ,分别交 , 于点 , ,连接 .有下列结论:① ;② ;③ ;④ .其中正确的是( )
A、 B、 C、 D、10. 如图,正方形 的边 ,对角线 和 交于点 , 是边 上靠近点 的三等分点,连接 , ,分别交 , 于点 , ,连接 .有下列结论:① ;② ;③ ;④ .其中正确的是( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
11. 因式分解: .12. 若 ,则a-b= .13. 已知点 在第一象限,到x轴的距离为2,则m= .14. 已知 ,求 的值为 .15. 如图,正五边形ABCDE的边长为5,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则 的长为 .
 16. 如图,在 中, 平分 , ,垂足为 , 为 的中点.若 , ,则 的长为 .
16. 如图,在 中, 平分 , ,垂足为 , 为 的中点.若 , ,则 的长为 . 17. 如图,半径为 的 中, 为直径,弦 且过半径 的中点,点 为 上一动点, 于点 .当点 从点 出发顺时针运动到点 时,点 所经过的路径长为 .
17. 如图,半径为 的 中, 为直径,弦 且过半径 的中点,点 为 上一动点, 于点 .当点 从点 出发顺时针运动到点 时,点 所经过的路径长为 .
三、解答题
-
18. 先化简,再求值: ,其中 .19. 如图,AB 为⊙O 的直径,PD 切⊙O 于点 C,交 AB 的延长线于点 D,且∠D=2∠A.
 (1)、求∠D 的度数;(2)、若⊙O 的半径为 m,求 BD 的长.20. 对垃圾进行分类投放,能有效提高对垃圾的处理和再利用的效率,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成 , , , 四组,绘制了如下统计图表:
(1)、求∠D 的度数;(2)、若⊙O 的半径为 m,求 BD 的长.20. 对垃圾进行分类投放,能有效提高对垃圾的处理和再利用的效率,减少污染,保护环境.为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成 , , , 四组,绘制了如下统计图表:“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
38
72
60
m
“垃圾分类知识及投放情况”问卷测试成绩统计图

依据以上统计信息解答下列问题:
(1)、填空:m= , n=;(2)、为了增强大家对垃圾分类的了解,学校组织每个班级学习相关知识,经过一段时间的学习后,再次对原来抽取的这些同学进行问卷测试,发现 A 组的同学平均成绩提高 15 分, B 组的同学平均成绩提高10分, C 组的同学平均成绩提高5分, D 组的同学平均成绩没有变化,请估计学习后这些同学的平均成绩提高多少分?若把测试成绩超过85分定为优秀,这些同学再次测试的平均成绩是否达到优秀,为什么?21. 已知关于 的一元二次方程 .( )求证:方程总有两个实数根;
22. 某种型号油电混合动力汽车,从A地到B地燃油行驶需纯燃油费用76元,从A地到B地用电行驶需纯用电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少需用电行驶多少千米?23. 如图,在 中, ,顶点 , 都在反比例函数 的图象上,直线 轴,垂足为 ,连接 , . (1)、若 , ,求 的值;(2)、若 ,求直线 的解析式.24. 在平面直角坐标系中,矩形 的顶点A , C分别在x轴、y轴上,点B的坐标为 ,将矩形 绕点A顺时针旋转 ,得到矩形 ,点O , B , C的对应点分别为 .
(1)、若 , ,求 的值;(2)、若 ,求直线 的解析式.24. 在平面直角坐标系中,矩形 的顶点A , C分别在x轴、y轴上,点B的坐标为 ,将矩形 绕点A顺时针旋转 ,得到矩形 ,点O , B , C的对应点分别为 .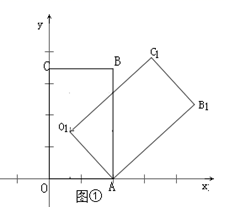
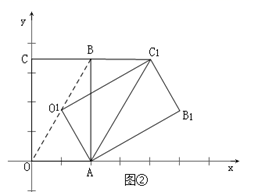 (1)、如图①,当 时, 与 相交于点E , 求点E的坐标;(2)、如图②,当点 落在对角线 上时,连接 ,四边形 是何特殊的四边形?并说明理由;(3)、连接 ,当 取得最小值和最大值时,分别求出点 的坐标(直接写出结果即可).25. 如图,抛物线 交 轴于 、 两点,交 轴于点 .直线 经过点 、 .
(1)、如图①,当 时, 与 相交于点E , 求点E的坐标;(2)、如图②,当点 落在对角线 上时,连接 ,四边形 是何特殊的四边形?并说明理由;(3)、连接 ,当 取得最小值和最大值时,分别求出点 的坐标(直接写出结果即可).25. 如图,抛物线 交 轴于 、 两点,交 轴于点 .直线 经过点 、 .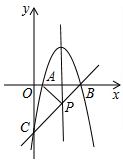 (1)、求抛物线的解析式;(2)、抛物线的对称轴 与直线 相交于点 ,连接 、 ,判定 的形状,并说明理由;(3)、在直线 上是否存在点 ,使 与直线 的夹角等于 的2倍?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、抛物线的对称轴 与直线 相交于点 ,连接 、 ,判定 的形状,并说明理由;(3)、在直线 上是否存在点 ,使 与直线 的夹角等于 的2倍?若存在,请求出点 的坐标;若不存在,请说明理由.