安徽省合肥市重点中学2021年中考数学三模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 的相反数是( ).A、 B、 C、 D、2. 下列各式计算正确的是( )A、 B、 C、 D、3. 据统计,某城市去年接待旅游人数约为89000000人,89000000这个数据用科学记数法表示为( )A、 B、 C、 D、4. 下面几个几何体,从正面看到的形状是圆的是( )A、
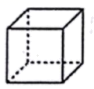 B、
B、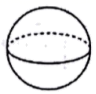 C、
C、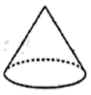 D、
D、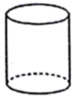 5. 某中学八(1)班8个同学在课间进行一分钟跳绳比赛,成绩(单位:个)如下:115,138,126,143,134,126,157,118.这组数据的众数和中位数分别是( )A、126,126 B、126,130 C、130,134 D、118,1346. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )A、相等 B、互余或互补 C、互补 D、相等或互补7. 下列关于二次函数 ( )的图象与x轴交点的判断,正确的是( )A、只有一个交点,且它位于y轴的右侧 B、只有一个交点,且它位于y轴的左侧 C、有两个交点,且它们位于y轴的两侧 D、有两个交点,且它们位于y轴的右侧8. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
5. 某中学八(1)班8个同学在课间进行一分钟跳绳比赛,成绩(单位:个)如下:115,138,126,143,134,126,157,118.这组数据的众数和中位数分别是( )A、126,126 B、126,130 C、130,134 D、118,1346. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )A、相等 B、互余或互补 C、互补 D、相等或互补7. 下列关于二次函数 ( )的图象与x轴交点的判断,正确的是( )A、只有一个交点,且它位于y轴的右侧 B、只有一个交点,且它位于y轴的左侧 C、有两个交点,且它们位于y轴的两侧 D、有两个交点,且它们位于y轴的右侧8. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
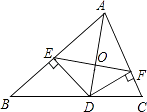 A、①②③ B、②③④ C、①③④ D、①②③④9. 如图,矩形 中, , ,动点M满足: ,则点M到点A、B的距离之和( )的最小值是( )
A、①②③ B、②③④ C、①③④ D、①②③④9. 如图,矩形 中, , ,动点M满足: ,则点M到点A、B的距离之和( )的最小值是( ) A、 B、 C、10 D、810. 如图,矩形 中,点 在 上,且 平分 , , ,则矩形 的面积为( )
A、 B、 C、10 D、810. 如图,矩形 中,点 在 上,且 平分 , , ,则矩形 的面积为( )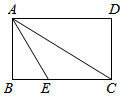 A、 B、24 C、 D、12
A、 B、24 C、 D、12二、填空题
-
11. 把多项式 分解因式的结果是 .12. 如图,点A,B,C都在⊙O上,若OB=3,∠ABC=30°,则劣弧AC的长为.
 13. 如图,反比例函数 的图象位于第一、三象限,且图象上的点与坐标轴围成的矩形面积为2,请你在第三象限的图象上取一个正确的点,并写出它的坐标 .
13. 如图,反比例函数 的图象位于第一、三象限,且图象上的点与坐标轴围成的矩形面积为2,请你在第三象限的图象上取一个正确的点,并写出它的坐标 . 14. 如图,已知在△ABC中,∠C=90°,BC=2,点D是边BC的中点,∠ABC=∠CAD,将ACD沿直线AD翻折,点C落在点E处,连结BE,那么线段BE的长为 .
14. 如图,已知在△ABC中,∠C=90°,BC=2,点D是边BC的中点,∠ABC=∠CAD,将ACD沿直线AD翻折,点C落在点E处,连结BE,那么线段BE的长为 .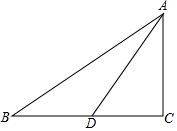
三、解答题
-
15. 解不等式: ,并把它的解集在数轴上表示出来.16. 学校为奖励在艺术节系列活动中表现优秀的同学,计划购买甲、乙两种奖品.已知购买甲种奖品30件和乙种奖品25件需花费1950元,购买甲种奖品15件和乙种奖品35件需花费1650元.(1)、求甲、乙两种奖品的单价;(2)、学校计划购买甲、乙两种奖品共1800件,其中购买乙种奖品的件数不超过甲种奖品件数的2倍,学校分别购买甲、乙两种奖品多少件才能使总费用最小?最小费用是多少元?17. 如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系.△ABC的顶点都在格点上.
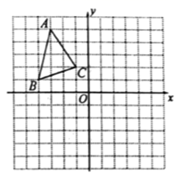 (1)、将△ABC 向右平移 6个单位长度得到△A1B1C1 , 请画出△A1B1C1;(2)、画出△A1B1C1关于点O的中心对称图形△A2B2C2:(3)、若将△ABC 绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.18. 观察下列等式:
(1)、将△ABC 向右平移 6个单位长度得到△A1B1C1 , 请画出△A1B1C1;(2)、画出△A1B1C1关于点O的中心对称图形△A2B2C2:(3)、若将△ABC 绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.18. 观察下列等式:① ;② ;③ ;④ ;⑤ ……
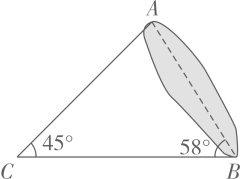
(1)、请按以上规律写出第⑥个等式;(2)、猜想并写出第n个等式 ▲ ;并证明猜想的正确性.(3)、利用上述规律,计算: = .19. 如图, 两点被池塘隔开,在 外选一点C , 连接 .测得 , , .根据测得的数据,求 的长(结果取整数).参考数据: , , .
 20. 如图,在△ABC中,∠ACB=90°,点O在边BC上,以点O为圆心,OB为半径的⊙O交AB于点E,D为⊙O上一点,点B是弧DE中点.
20. 如图,在△ABC中,∠ACB=90°,点O在边BC上,以点O为圆心,OB为半径的⊙O交AB于点E,D为⊙O上一点,点B是弧DE中点. (1)、如图1,若AE=BE,求证:四边形ACDE是平行四边形;(2)、如图2,若OB=OC,BE=2AE,求tan∠CAD的值.21. 在甲、乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字2,3,4,5,乙口袋中的小球上分别标有数字3,4,5,小明先从甲袋中任意摸出一个小球,记下数字为 ,小张从乙袋中任意摸出一个小球,记下数字为 .(1)、从甲袋摸出一个小球,则小球上的数字使代数式 的值为0的概率;(2)、若m,n都是方程 的解时,则小明获胜;若 , 都不是方程 的解时,则小张获胜;问他们两人谁获胜的概率大.22. 某游乐园要建造一个直径为20m的圆形喷水池,计划在喷水池周边安装一圈喷水头,使喷出的水柱距池中心4m处达到最高,最大高度为6m.如图,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)、如图1,若AE=BE,求证:四边形ACDE是平行四边形;(2)、如图2,若OB=OC,BE=2AE,求tan∠CAD的值.21. 在甲、乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字2,3,4,5,乙口袋中的小球上分别标有数字3,4,5,小明先从甲袋中任意摸出一个小球,记下数字为 ,小张从乙袋中任意摸出一个小球,记下数字为 .(1)、从甲袋摸出一个小球,则小球上的数字使代数式 的值为0的概率;(2)、若m,n都是方程 的解时,则小明获胜;若 , 都不是方程 的解时,则小张获胜;问他们两人谁获胜的概率大.22. 某游乐园要建造一个直径为20m的圆形喷水池,计划在喷水池周边安装一圈喷水头,使喷出的水柱距池中心4m处达到最高,最大高度为6m.如图,以水平方向为x轴,喷水池中心为原点建立直角坐标系. (1)、若要在喷水池的中心设计一个装饰物,使各方向喷出的水柱在此汇合,则这个装饰物的高度为多少,请计算说明理由.(2)、为了增加喷水池的观赏性,游乐园新增加了一批向上直线型喷射的喷水头,这些喷水头以水池为圆心,分别以1.5米,3米,4.5米,6米,7.5米为半径呈圆形放置,为了保证喷水时互不干扰,防止水花四溅,且所有直线喷水头射程高度均为一致,则直线型喷水头最高喷射高度为多少米?(假设所有喷水头高度忽略不计).23. 如图1,正方形ABCD和正方形AEFG,连接DG,BE
(1)、若要在喷水池的中心设计一个装饰物,使各方向喷出的水柱在此汇合,则这个装饰物的高度为多少,请计算说明理由.(2)、为了增加喷水池的观赏性,游乐园新增加了一批向上直线型喷射的喷水头,这些喷水头以水池为圆心,分别以1.5米,3米,4.5米,6米,7.5米为半径呈圆形放置,为了保证喷水时互不干扰,防止水花四溅,且所有直线喷水头射程高度均为一致,则直线型喷水头最高喷射高度为多少米?(假设所有喷水头高度忽略不计).23. 如图1,正方形ABCD和正方形AEFG,连接DG,BE (1)、[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是;位置关系是;(2)、[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;(3)、[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB= ,AE=1,求线段DG的长
(1)、[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是;位置关系是;(2)、[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;(3)、[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB= ,AE=1,求线段DG的长