安徽省合肥市肥东县2021年中考数学二模试卷
试卷更新日期:2021-07-28 类型:中考模拟
一、单选题
-
1. 实数2的相反数等于( )A、-2 B、 C、2 D、-2. 化简(-mn2)3结果正确的是( )A、m3n6 B、-m3n6 C、-mn6 D、-m4n53. 安徽省2020年全年城镇新增就业66.3万人,其中66.3万用科学记数法表示为( )A、66.3×103 B、66.3×104 C、6.63×105 D、6.63×1064. 如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
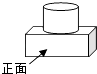 A、
A、 B、
B、 C、
C、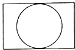 D、
D、 5. 已知一组数据1、 0 、3 、-1、 x、 2、 3的平均数是1,则这组数据的中位数是( )A、-1 B、1 C、3 D、-1或36. 中国古代数学著作《孙子算经》中有一道题:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆乘坐3人,则空余2辆车;若每辆车乘坐2人,则剩有9个人要步行.问人和车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、7. 如图,AB//CD//EF , 下列等式成立的是( )
5. 已知一组数据1、 0 、3 、-1、 x、 2、 3的平均数是1,则这组数据的中位数是( )A、-1 B、1 C、3 D、-1或36. 中国古代数学著作《孙子算经》中有一道题:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆乘坐3人,则空余2辆车;若每辆车乘坐2人,则剩有9个人要步行.问人和车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、7. 如图,AB//CD//EF , 下列等式成立的是( ) A、AC·CE=BD·DF B、AC·AE=BD·BF C、AC·DF=CE·BD D、CD2=AB·EF8. 在平面直角坐标系中,函数y=kx-1与 的图象相交,其中有一个交点为P(2,m),点A(x1 , y1)在y=kx-1图象上.点B(x2 , y2)在 图象上,下列说法正确的是( )A、当x1=x2< 2时,y1< y2 B、当x1=x2> 2时,y1< y2 C、当y1=y2< 1时,x1> x2 D、当y1=y2 > 1时,x1 > x29. 如图是两个同心圆,大圆的直径AC固定不动,小圆的直径BD绕着圆心0旋转,BD与AC不在同一条直线上,在BD旋转过程中,下面说法正确的是( )
A、AC·CE=BD·DF B、AC·AE=BD·BF C、AC·DF=CE·BD D、CD2=AB·EF8. 在平面直角坐标系中,函数y=kx-1与 的图象相交,其中有一个交点为P(2,m),点A(x1 , y1)在y=kx-1图象上.点B(x2 , y2)在 图象上,下列说法正确的是( )A、当x1=x2< 2时,y1< y2 B、当x1=x2> 2时,y1< y2 C、当y1=y2< 1时,x1> x2 D、当y1=y2 > 1时,x1 > x29. 如图是两个同心圆,大圆的直径AC固定不动,小圆的直径BD绕着圆心0旋转,BD与AC不在同一条直线上,在BD旋转过程中,下面说法正确的是( )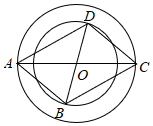 A、∠ADC的大小始终不变 B、四边形ABCD存在是矩形的情形 C、四边形ABCD的最大面积等于 AC·BD . D、AD的最大值等于 (AC+BD)10. 如图①,在矩形ABCD中,AB< AD , 对角线AC、BD相交于点O , 动点P从点A出发,沿A→B→C→D向点D运动.设点P的运动路程为x , ΔAOP的面积为y , y与x的函数关系图象如图②所示,则下列结论错误的是( )
A、∠ADC的大小始终不变 B、四边形ABCD存在是矩形的情形 C、四边形ABCD的最大面积等于 AC·BD . D、AD的最大值等于 (AC+BD)10. 如图①,在矩形ABCD中,AB< AD , 对角线AC、BD相交于点O , 动点P从点A出发,沿A→B→C→D向点D运动.设点P的运动路程为x , ΔAOP的面积为y , y与x的函数关系图象如图②所示,则下列结论错误的是( ) A、四边形ABCD的面积为12 B、AD边的长为4 C、当x=2.5时,△AOP是等边三角形 D、ΔAOP的面积为3时,x的值为3或10
A、四边形ABCD的面积为12 B、AD边的长为4 C、当x=2.5时,△AOP是等边三角形 D、ΔAOP的面积为3时,x的值为3或10二、填空题
-
11. 的解集是;12. 十二边形的内角和是13. 如图,一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接,主悬钢索是抛物线形状,两端到桥面的距离OM与AN相等.小强骑自行车从桥的一端0沿直线匀速穿过桥面到达另一端A , 当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同,那么他通过整个桥面OA共需秒.
 14. 如图,在ΔABC中,∠A=90°,∠BCD= ∠BCA , BD⊥DC于点D , DC交AB于点E , 请完成下列探究:
14. 如图,在ΔABC中,∠A=90°,∠BCD= ∠BCA , BD⊥DC于点D , DC交AB于点E , 请完成下列探究: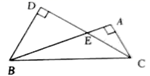 (1)、若∠BCD=n°,那么∠EBD=° (结果用含n的代数式表示);(2)、若 =m , 那么 =(结果用含m的代数式表示);
(1)、若∠BCD=n°,那么∠EBD=° (结果用含n的代数式表示);(2)、若 =m , 那么 =(结果用含m的代数式表示);三、解答题
-
15. 计算:16. 如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点和O点都在小正方形的顶点上.
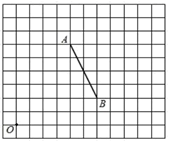 (1)、将线段AB绕点B逆时针旋转90°,画出旋转后得到的线段A1B;(2)、以点O为位似中心,在网格图中将线段AB缩小为原来的 ,画出缩小后的线段A2B1(点A、B分别与A2、B1对应).17. 观察下列等式:
(1)、将线段AB绕点B逆时针旋转90°,画出旋转后得到的线段A1B;(2)、以点O为位似中心,在网格图中将线段AB缩小为原来的 ,画出缩小后的线段A2B1(点A、B分别与A2、B1对应).17. 观察下列等式:第1个等式: ; 第2个等式: ;
第3个等式: ; 第4个等式: ;
第5个等式: ;
按照以
上规律,解决下列问题:
(1)、写出第6个等式: .(2)、写出你猜想的第 个等式: ▲ . (用含 的等式表示),并证明.18. 某商品一月份价格为a元/件,二月份降价,三月份又涨价,涨价后恢复到一月份的价格.如果三月份涨价的百分比是二月份降价百分比的2倍,求二月份降价的百分比.19. 如图1是一插着吸管的酸奶杯子,图2是它的截面图(截面经过杯口和杯底的圆心).其中杯壁长AB=10cm,AB与桌面EF的夹角∠ABF=83°,吸管NC经过点A且与桌面EF的夹角∠NCF=45°,求杯子的高AM和杯底的直径BC . (结果精确到0.1cm,参考数据: sin83°≈0.993,cos83°≈0.122,tan83°≈8.144)
 20. 如图,四边形ABCD内接于⊙O , AD是直径,AC平分∠BAD , 过点C作⊙O的切线,与AB的延长线交于点E .
20. 如图,四边形ABCD内接于⊙O , AD是直径,AC平分∠BAD , 过点C作⊙O的切线,与AB的延长线交于点E . (1)、求证:∠E=90°;(2)、若⊙O的半径长为4,AC长为7,求BC的长;21. 争创文明县城,从我做起.某校在八年级开设了文明礼仪校本课程,为了了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:
(1)、求证:∠E=90°;(2)、若⊙O的半径长为4,AC长为7,求BC的长;21. 争创文明县城,从我做起.某校在八年级开设了文明礼仪校本课程,为了了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:整理上面的数据,得到频数分布表和扇形统计图:
94
83
90
86
94
88
96
100
89
82
94
82
84
89
88
93
98
94
93
92
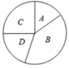
等级
A
B
C
D
成绩/分
95≤x≤100
90≤x< 95
85≤x< 90
80≤x< 85
频数
3
a
b
4
根据以上信息,解答下列问题:
(1)、填空: a=; b= .扇形统计图中表示A等级的扇形的圆心角= ;(2)、若成绩不低于90分为优秀,请估计该校1200名八年级学生中,达到优秀等级的人数;(3)、已知A等级中有两名女生,现从A等级中随机抽取2名同学,请用列表或者画柯状图的方法求出恰好抽到一男一女的概率.22. 春节期间商家销售某种纪念品,进价为12元/只,售价为20元/只,为了促销,该商家决定凡是一次购买10只以上的,每多买一只,售价就降低0.10元[例如:某人买20只这种纪念品,于是每只降价 元,就可以按19元/只的价格购买],但是最低价为16元/只,(1)、求顾客一次至少购买多少只,才能以最低价购买?(2)、求出当一次购买 只时,总利润 (元)与购买量 (只)之间的函数关系式;(3)、有一天,一位顾客一次购买了46只,另一位顾客一次购买了50只,商家发现卖了50只反而比卖46只赚的钱少,为了使每次卖的数量越多赚的钱也越多,在其他促销条件不变的情况下,最低价16元/只至少要提高到多少?为什么?23. 已知:在正方形ABCD中,点E、F、G分别在BC、AB和CD上,FG⊥ED , 垂足为点H . (1)、如图1,点G与点C重合,求证: FG=ED;(2)、如图2,点G与点C不重合,延长FG交BC的延长线于点M , 若H为FM的中点,求证:AF=CM;(3)、如图3,在(2)的条件下,取AD的中点N , 连接HN , 若BF=2AF , HN= ,求EM的长.
(1)、如图1,点G与点C重合,求证: FG=ED;(2)、如图2,点G与点C不重合,延长FG交BC的延长线于点M , 若H为FM的中点,求证:AF=CM;(3)、如图3,在(2)的条件下,取AD的中点N , 连接HN , 若BF=2AF , HN= ,求EM的长.