辽宁省丹东市2021年中考数学试卷
试卷更新日期:2021-07-28 类型:中考真卷
一、单选题
-
1. -5的相反数是( )A、5 B、 C、-5 D、0.52. 下列运算正确的是( )A、 B、 C、 D、3. 如图是由几个完全相同的小正方体组成的立体图形,它的俯视图是( )
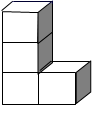 A、
A、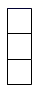 B、
B、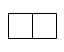 C、
C、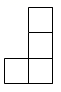 D、
D、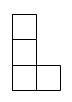 4. 若一组数据1,3,4,6,m的平均数为4,则这组数据的中位数和众数分别是( )A、4,6 B、4,4 C、3,6 D、3,45. 若实数k、b是一元二次方程 的两个根,且 ,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在矩形 中,连接 ,将 沿对角线 折叠得到 交 于点O , 恰好平分 ,若 ,则点O到 的距离为( )
4. 若一组数据1,3,4,6,m的平均数为4,则这组数据的中位数和众数分别是( )A、4,6 B、4,4 C、3,6 D、3,45. 若实数k、b是一元二次方程 的两个根,且 ,则一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在矩形 中,连接 ,将 沿对角线 折叠得到 交 于点O , 恰好平分 ,若 ,则点O到 的距离为( ) A、 B、2 C、 D、37. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )
A、 B、2 C、 D、37. 如图,点A在曲线到 上,点B在双曲线 上, 轴,点C是x轴上一点,连接 、 ,若 的面积是6,则k的值( )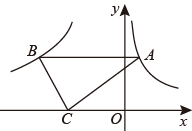 A、-6 B、-8 C、-10 D、-128. 已知抛物线 ,且 .判断下列结论:① ;② ;③抛物线与x轴正半轴必有一个交点;④当 时, ;⑤该抛物线与直线 有两个交点,其中正确结论的个数( )A、2 B、3 C、4 D、5
A、-6 B、-8 C、-10 D、-128. 已知抛物线 ,且 .判断下列结论:① ;② ;③抛物线与x轴正半轴必有一个交点;④当 时, ;⑤该抛物线与直线 有两个交点,其中正确结论的个数( )A、2 B、3 C、4 D、5二、填空题
-
9. 按照现行贫困标准计算,中国770000000村贫困人口摆脱贫困,将数据770000000用科学记数法表示为 .10. 在函数 中,自变量x的取值范围 .11. 分解因式:ma2+2mab+mb2=.12. 关于x的一元二次方程 有两个不相等的实数根,则 的取值范围是.
13. 不等式组 无解,则m的取值范围 .14. 如图,在 中, 的垂直平分线交 于点D , 交 于点 ,点F是 的中点,连接 、 ,若 ,则 的周长为 .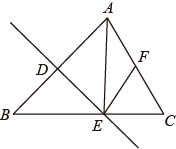 15. 如图,在矩形 中,连接 ,过点C作 平分线 的垂线,垂足为点E , 且交 于点F;过点C作 平分线 的垂线,垂足为点H , 且交 于点G , 连接 ,若 , ,则线段 的长度为 .
15. 如图,在矩形 中,连接 ,过点C作 平分线 的垂线,垂足为点E , 且交 于点F;过点C作 平分线 的垂线,垂足为点H , 且交 于点G , 连接 ,若 , ,则线段 的长度为 . 16. 已知:到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果 是锐角(或直角)三角形,则其费马点P是三角形内一点,且满足 .(例如:等边三角形的费马点是其三条高的交点).若 ,P为 的费马点,则 ;若 ,P为 的费马点,则 .
16. 已知:到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果 是锐角(或直角)三角形,则其费马点P是三角形内一点,且满足 .(例如:等边三角形的费马点是其三条高的交点).若 ,P为 的费马点,则 ;若 ,P为 的费马点,则 .三、解答题
-
17. 先化简,再求代数式的值: ,其中 .18. 如图,在 中,点O是 的中点,连接 并延长交 的延长线于点E , 连接 、 .
 (1)、求证:四边形 是平行四边形;(2)、若 ,判断四边形 的形状,并说明理由.19. 某中学为了增强学生体质,计划开设A:跳绳,B:毽球,C:篮球,D:足球四种体育活动,为了解学生对这四种体育活动的喜欢情况,对部分学生进行抽样调查(每人只能选择一种体育活动),并绘制成如图所示的两幅不完全的统计图,根据图中所给信息解答下列问题:
(1)、求证:四边形 是平行四边形;(2)、若 ,判断四边形 的形状,并说明理由.19. 某中学为了增强学生体质,计划开设A:跳绳,B:毽球,C:篮球,D:足球四种体育活动,为了解学生对这四种体育活动的喜欢情况,对部分学生进行抽样调查(每人只能选择一种体育活动),并绘制成如图所示的两幅不完全的统计图,根据图中所给信息解答下列问题: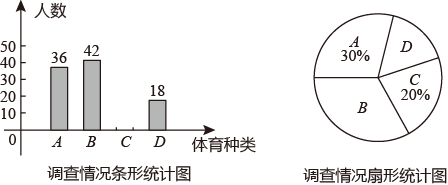 (1)、求这次抽样调查的学生有多少人?(2)、求出B所在扇形圆心角的度数,并将条形统计图补充完整;(3)、若该校有800名学生,请根据抽样调查结果估计喜欢B的人数.20. 一个不透明的袋子中装有4个只有颜色不同的小球,其中2个红球,2个白球,摇匀后从中一次性摸出两个小球.(1)、请用列表格或画树状图的方法列出所有可能性;(2)、若摸到两个小球的颜色相同,甲获胜;摸到两个小球颜色不同,乙获胜.这个游戏对甲、乙双方公平吗?请说明理由.21. 为落实“乡村振兴计划”的工作要求,某区政府计划对乡镇道路进行改造,安排甲、乙两个工程队完成,已知乙队比甲队每天少改造20米,甲队改造400米的道路与乙队改造300米的道路所用时间相同,求甲、乙两个工程队每天改造的道路长度分别是多少米?22. 如图, 是 的外接圆,点D是 的中点,过点D作 分别交 、 的延长线于点E和点F , 连接 、 , 的平分线 交 于点M .
(1)、求这次抽样调查的学生有多少人?(2)、求出B所在扇形圆心角的度数,并将条形统计图补充完整;(3)、若该校有800名学生,请根据抽样调查结果估计喜欢B的人数.20. 一个不透明的袋子中装有4个只有颜色不同的小球,其中2个红球,2个白球,摇匀后从中一次性摸出两个小球.(1)、请用列表格或画树状图的方法列出所有可能性;(2)、若摸到两个小球的颜色相同,甲获胜;摸到两个小球颜色不同,乙获胜.这个游戏对甲、乙双方公平吗?请说明理由.21. 为落实“乡村振兴计划”的工作要求,某区政府计划对乡镇道路进行改造,安排甲、乙两个工程队完成,已知乙队比甲队每天少改造20米,甲队改造400米的道路与乙队改造300米的道路所用时间相同,求甲、乙两个工程队每天改造的道路长度分别是多少米?22. 如图, 是 的外接圆,点D是 的中点,过点D作 分别交 、 的延长线于点E和点F , 连接 、 , 的平分线 交 于点M . (1)、求证: 是 的切线;(2)、若 , ,求线段 的长.23. 如图,一架无人机在空中A处观测到山顶B的仰角为 ,山顶B在水中的倒影C的俯角为 ,此时无人机距水面的距离 米,求点B到水面距离 的高度.
(1)、求证: 是 的切线;(2)、若 , ,求线段 的长.23. 如图,一架无人机在空中A处观测到山顶B的仰角为 ,山顶B在水中的倒影C的俯角为 ,此时无人机距水面的距离 米,求点B到水面距离 的高度.(参考数据: , , , , , )
 24. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(2)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?(3)、超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?25. 已知 , 在正方形 中,点M、N为对角线 上的两个动点 , 且 ,过点M、N分别作 、 的垂线相交于点E , 垂足分别为F、G , 设 的面积为 , 的面积为 , 的面积为 .
24. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(2)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?(3)、超市的销售人员发现:当该商品每月销售量超过某一数量时,会出现所获利润反而减小的情况,为了每月所获利润最大,该商品销售单价应定为多少元?25. 已知 , 在正方形 中,点M、N为对角线 上的两个动点 , 且 ,过点M、N分别作 、 的垂线相交于点E , 垂足分别为F、G , 设 的面积为 , 的面积为 , 的面积为 .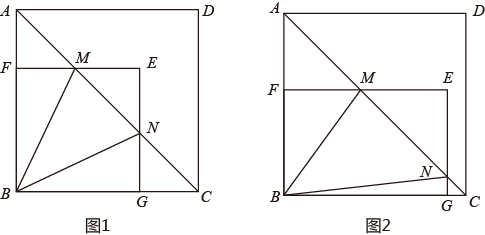 (1)、如图1,当四边形 为正方形时,
(1)、如图1,当四边形 为正方形时,①求证: ;
②求证: ;
(2)、如图2,当四边形 为矩形时,写出 , , 三者之间的数量关系,并说明理由;(3)、在(2)的条件下,若 , 请直接写出 的值.26. 如图,已知点 ,点 ,直线 过点B交y轴于点C , 交x轴于点D , 抛物线 经过点A、C、D , 连接 、 .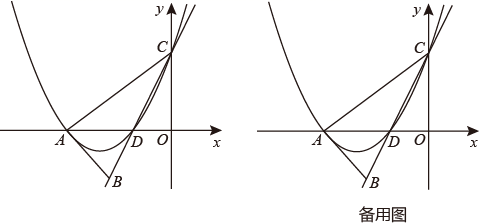 (1)、求抛物线的表达式;(2)、判断 的形状,并说明理由;(3)、E为直线 上方的抛物线上一点,且 ,求点E的坐标;(4)、N为线段 上的动点,动点P从点B出发,以每秒1个单位长度的速度沿线段 运动到点N , 再以每秒 个单位长度的速度沿线段 运动到点C , 又以每秒1个单位长度的速度沿线段 向点O运动,当点P运动到点O后停止,请直接写出上述运动时间的最小值及此时点N的坐标.
(1)、求抛物线的表达式;(2)、判断 的形状,并说明理由;(3)、E为直线 上方的抛物线上一点,且 ,求点E的坐标;(4)、N为线段 上的动点,动点P从点B出发,以每秒1个单位长度的速度沿线段 运动到点N , 再以每秒 个单位长度的速度沿线段 运动到点C , 又以每秒1个单位长度的速度沿线段 向点O运动,当点P运动到点O后停止,请直接写出上述运动时间的最小值及此时点N的坐标.