初中数学浙教版八年级上册2.4 等腰三角形的判定定理 同步练习
试卷更新日期:2021-07-27 类型:同步测试
一、单选题
-
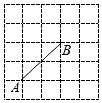
1. 下列说法错误的是( )A、有两边相等的三角形是等腰三角形 B、直角三角形不可能是等腰三角形 C、有两个角为60°的三角形是等边三角形 D、有一个角为60°的等腰三角形是等边三角形2. 一个角是 的等腰三角形是( )A、等腰直角三角形 B、等边三角形 C、直角三角形 D、上述都正确3. 如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )
 A、4 B、5 C、6 D、74. 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A、4 B、5 C、6 D、74. 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( ) A、∠M=∠N B、AM∥CN C、AC=BD D、AM=CN5. 如图, 中, , ,在直线 或 上取一点P,使 为等腰三角形,则符合条件的点P共有( )
A、∠M=∠N B、AM∥CN C、AC=BD D、AM=CN5. 如图, 中, , ,在直线 或 上取一点P,使 为等腰三角形,则符合条件的点P共有( ) A、 个 B、 个 C、 个 D、 个6. 已知:如图,下列三角形中, ,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的有( )
A、 个 B、 个 C、 个 D、 个6. 已知:如图,下列三角形中, ,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的有( ) A、1个 B、2个 C、3个 D、4个7. 如图, 中, , , ,则 的周长为( )
A、1个 B、2个 C、3个 D、4个7. 如图, 中, , , ,则 的周长为( ) A、9 B、8 C、6 D、128. 如图,点 是 的 , 的平分线的交点, 交 于点 , 交 于点 ,若 的周长为 ,那么 的长为( )
A、9 B、8 C、6 D、128. 如图,点 是 的 , 的平分线的交点, 交 于点 , 交 于点 ,若 的周长为 ,那么 的长为( )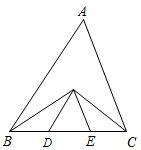 A、 B、 C、 D、9. 在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )A、4个 B、3个 C、2个 D、1个10. 已知 是 的两边,且 ,则 的形状是( )A、等腰三角形 B、等边三角形 C、锐角三角形 D、不确定
A、 B、 C、 D、9. 在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )A、4个 B、3个 C、2个 D、1个10. 已知 是 的两边,且 ,则 的形状是( )A、等腰三角形 B、等边三角形 C、锐角三角形 D、不确定二、填空题
-
11. 已知在 中, ,如要判定 是等边三角形,还需添加一个条件.现有下面三种说法:①如果添加条件“ ”,那么 是等边三角形;②如果添加条件“ ”,那么 是等边三角形;③如果添加条件“边 、 上的高相等”那么 是等边三角形.上述说法中,正确的有 . (填序号)12. 如图,长方形ABCD中,AB=6,BC=2,直线l是长方形ABCD的一条对称轴,且分别与AD,BC交于点E,F,若直线l上的动点P,使得△PAB和△PBC均为等腰三角形.则动点P的个数有个.
 13. 如图,在△ABC中,AB=8,BC=6,AC=5,∠B、∠C的角平分线相交于点D,过D作EF//BC交AB于点E,交AC于点F,则△AEF的周长等于
13. 如图,在△ABC中,AB=8,BC=6,AC=5,∠B、∠C的角平分线相交于点D,过D作EF//BC交AB于点E,交AC于点F,则△AEF的周长等于 14. 如图所示,在△ABC中,∠ABC,∠ACB的平分线相交于点D,过点D作EF∥BC交AB于点E,交AC于点E.若AB+AC=20,可求得△AEF的周长为 .
14. 如图所示,在△ABC中,∠ABC,∠ACB的平分线相交于点D,过点D作EF∥BC交AB于点E,交AC于点E.若AB+AC=20,可求得△AEF的周长为 . 15. 如图, 是边长为 的等边三角形, 是 内的任意一点,分别过点 作 分别交 , 于点 , ,作 分别交 , 于点 , ,作 分别交 , 于点 , .则 的值为 .
15. 如图, 是边长为 的等边三角形, 是 内的任意一点,分别过点 作 分别交 , 于点 , ,作 分别交 , 于点 , ,作 分别交 , 于点 , .则 的值为 . 16. 如图,在 中, 分别为 的中点.若 ,则 的长度为.
16. 如图,在 中, 分别为 的中点.若 ,则 的长度为.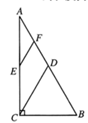
三、解答题
-
17. 阅读材料:已知△ABC中,AD平分∠BAC,AD是△ABC的中线,求证:AB=AC.
小明根据已知条件发现若AD平分∠BAC可得∠BAD=∠CAD,又AD是△ABC的中线,可得BD=CD,加上公共边的条件AD=AD,有两条边和一个角对应相等,就下结论得到△ABD和△ACD是全等的,从而得到结论∠B=∠C,可证出AB=AC成立;小芳的方法是用角平分线的性质得到DE=DF,再用中线分三角形的面积为相等两部分,再用等面积的方法可以得到结论.请你回答小明和小芳的证明思路谁正确的?请任选择一个方法进行完整的证明(可以与小明和小芳的方法不同)
 18. 如图, 中, ,点 是 延长线上一点, 于点 交 于点 ,求证: .
18. 如图, 中, ,点 是 延长线上一点, 于点 交 于点 ,求证: . 19. 如图,△ABC是等边三角形,D是边AC的中点,EC⊥BC与点C,连接BD、DE、AE且CE=BD,
19. 如图,△ABC是等边三角形,D是边AC的中点,EC⊥BC与点C,连接BD、DE、AE且CE=BD,求证:△ADE为等边三角形
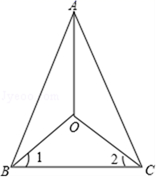
 20. 如图△ABC中, 的平分线交于点O,过O点做 ,交AB、AC于E、F,请写出图中线段EF与BE、CF间的数量关系,并说明理由.
20. 如图△ABC中, 的平分线交于点O,过O点做 ,交AB、AC于E、F,请写出图中线段EF与BE、CF间的数量关系,并说明理由. 21. 如图,一船上午 时从海岛 出发,以 海里/时的速度向正北方向航行, 时到达 处,从 、 两处分别望灯塔 ,测得 , ,求从 处到灯塔 的距离.
21. 如图,一船上午 时从海岛 出发,以 海里/时的速度向正北方向航行, 时到达 处,从 、 两处分别望灯塔 ,测得 , ,求从 处到灯塔 的距离.