重庆市沙坪坝区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 点（2，2）所在象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在今年校园足球比赛中，某校五支参赛球队进球数如下（单位：个）：3，4，5，4，2，这组数据的众数是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 在 $▱ A B C D$ 中，如果 $∠ A = 2 ∠ B$ ，那么 $∠ D$ 等于（）

A、 $30 °$ B、 $60 °$ C、 $90 °$ D、 $120 °$

查看试题解析
4. 函数 $y = \frac{1}{x - 2}$ 的自变量 $x$ 的取值范围是（）

A、 $x \neq 0$ B、 $x \neq 2$ C、 $x > 2$ D、 $x < 2$

查看试题解析
5. 矩形的一条边长为x，另一条边长为y，若它的周长是20，则y与x的函数关系式为（）

A、y＝10﹣x（0＜x＜10） B、y＝ $\frac{10}{x}$ （0＜x＜10） C、y＝20﹣x（0＜x＜20） D、y＝ $\frac{20}{x}$ （0＜x＜20）

查看试题解析
6. 某老师对班上甲、乙两位同学五次数学成绩进行统计，两人平均成绩均为115分，甲同学成绩的方差为15，乙同学成绩的方差为10，则下列说法正确的是（）

A、甲同学的成绩更稳定 B、乙同学的成绩更稳定 C、甲、乙两位同学的成绩一样稳定 D、不能确定两位同学的成绩稳定性

查看试题解析
7. 正方形具有而菱形不具有的性质是（）

A、四条边都相等 B、对角线互相垂直 C、两组对角分别相等 D、四个角都是直角

查看试题解析
8. 一元二次方程x²＋6x﹣5＝0配方后可化为（）

A、（x＋3）²＝5 B、（x＋3）²＝14 C、（x﹣3）²＝5 D、（x﹣3）²＝14

查看试题解析
9. 关于反比例函数y＝﹣ $\frac{6}{x}$ ，下列叙述正确的是（）

A、函数图象经过点（﹣2，﹣3） B、函数图象在第一、三象限 C、当x＞﹣2时，y＞3 D、当x＜0时，y随x的增大而增大

查看试题解析
10. 若a是关于x的方程3x²﹣x﹣1=0的一个根，则2021﹣6a²＋2a的值是（）

A、2023 B、2022 C、2020 D、2019

查看试题解析
11. 如图，AC，BD是▱ABCD的对角线，AC⊥CD，若BD﹣AC＝4，且AB＝4，则线段BC的长度为（）

A、 $\frac{36}{5}$ B、 $2 \sqrt{13}$ C、 $\frac{9}{2}$ D、 $2 \sqrt{5}$

查看试题解析
12. 某工厂中标生产一批5G手机配件的定单，该工厂未完成的定单任务量y（件）与生产时间x（天）之间的函数关系如图所示（AB∥CD，BC∥x轴）.下列结论：
（1）该工厂这批定单平均每天生产500件；（2）该工厂这批定单任务量是10000件；（3）该工厂生产这批定单中途停产了2天；（4）该工厂完成这批定单时间少于22天；其中一定正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 矩形的对称轴有条.

查看试题解析
14. 在平面直角坐标系中，若点A（2，﹣3）与点B关于x轴对称，则AB的长度为.

查看试题解析
15. 某校招聘教师，其中一名教师的笔试成绩是90分，面试成绩是80分，若笔试成绩与面试成绩在综合成绩中的权重分别是60%，40%，则该教师的综合成绩为分.

查看试题解析
16. 在菱形 $A B C D$ 中， $A C = 6$ ， $B D = 8$ ，则菱形 $A B C D$ 的周长是.

查看试题解析
17. 如图，在平面直角坐标系中，等腰Rt△ABC的顶点A、B分别在x轴、y轴上，反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图象经过直角顶点C.若OA＝7，OB＝3，则k的值为 .

查看试题解析
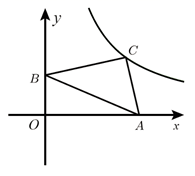18. 如图，在矩形ABCD中，点E在边BC上，连结AE，将△ABE沿直线AE翻折得到△AFE，EF与AC相交于点M.若AB＝8，BC＝10，且BE＝ $\frac{3}{5}$ BC，则点F到直线AD的距离为.

查看试题解析

三、解答题

19. 解下列方程：

(1)、x²﹣4x＝0；

(2)、2y²＋4y＝5

查看试题解析
20. 在第26个“世界读书日”来临之际，某学校开展了“书香满校园，阅读伴成长”的阅读知识竞赛活动，为了解竞赛情况，随机抽取了20名学生的成绩（竞赛成绩均为整数，满分10分），成绩如下：6，5，8，7，10，7，9，8，4，7，10，6，8，9，7，8，5，8，6，10
整理数据：

分数

4

5

6

7

8

9

10

学生人数

1

a

3

4

b

2

3

根据以上信息回答下列问题：

(1)、填空：a＝， b＝；

(2)、请求出这20名学生成绩的平均数和中位数；

(3)、抽取的20名学生中，小明的成绩为8分，你认为小明的成绩在抽取的20名学生的成绩中属于“中上”水平吗？请说明理由.

查看试题解析
21. 如图，在▱ABCD中，点E、F分别在边BC、AD上，且BE＝DF.

(1)、求证：四边形AECF是平行四边形；

(2)、若AE平分∠BAD，∠B＝70°，求∠DFC的度数.

查看试题解析

22. 探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程.以下是我们研究函数y＝|2x﹣2|﹣4性质及其应用的部分过程，请按要求完成下列各小题：

(1)、请直接写出如表中m，n的值，并在图中补全该函数图象；

x	……	﹣3	﹣2	﹣1	0	1	2	3	4	5	……
y＝\|2x﹣2\|﹣4	……	4	m	0	﹣2	﹣4	﹣2	0	n	4	……

(2)、结合函数图象，直接写出该函数的一条性质；

(3)、已知函数y＝

\frac{8}{x}

的图象如图所示，结合你所画的函数图象，直接写出不等式

\frac{8}{x} < | 2 x - 2 | - 4

的解集.

查看试题解析

23. 为缅怀革命英烈、传承红色基因，在今年“五一”小长假期间，各地游客纷纷来到重庆歌乐山烈士陵园瞻仰革命遗址.据统计，重庆歌乐山烈士陵园4月30日接待游客1.2万人次，5月2日接待游客2.7万人次.

(1)、求今年4月30日到5月2日，重庆歌乐山烈士陵园接待游客的日平均增长率；

(2)、由于暴雨天气，重庆歌乐山烈士陵园5月3日接待游客人次比5月2日减少了 $\frac{1}{3}$ ，5月4日天气放晴，接待游客人次比5月3日增加了6a%，又因假期即将结束，5月5日接待游客人次比5月4日减少了 $\frac{15}{4}$ a%，即使这样，5月5日接待游客人次还是比4月30日增加了50%，求a的值.

查看试题解析
24. 若关于x的一元二次方程（ax﹣b）（cx﹣d）＝0（ac≠0且a≠﹣1，c≠﹣1）的解x₁＝ $\frac{b}{a}$ ＝a﹣b，x₂＝ $\frac{d}{c}$ ＝c﹣d，则称该方程为二次“差解方程”.例如：（x﹣ $\frac{1}{2}$ ）（﹣3x+ $\frac{9}{2}$ ）＝0的解x₁＝ $\frac{1}{2}$ ，x₂＝ $\frac{3}{2}$ ，且 $\frac{1}{2}$ ＝1﹣ $\frac{1}{2}$ ， $\frac{3}{2}$ =﹣3﹣（﹣ $\frac{9}{2}$ ），所以该方程（x﹣ $\frac{1}{2}$ ）（﹣3x+ $\frac{9}{2}$ ）＝0是二次“差解方程”.
根据上述材料，解决下列问题：

(1)、判断方程（2x﹣ $\frac{4}{3}$ ）（﹣4x﹣ $\frac{16}{3}$ ）＝0是否是二次“差解方程”，并说明理由；

(2)、若关于x的方程（3x﹣mn﹣m）（﹣2x﹣mn＋n）＝0是二次“差解方程”，求关于y的一元二次方程m（y﹣1）＋n（y﹣m）＝ $\frac{{(m n - n)}^{2}}{4} y^{2}$ 的解.

查看试题解析
25. 在正方形ABCD中，点E、F分别在边BC，CD上，连结AE、AF.

(1)、如图1，过点E作EM⊥AF交AD于点M，求证：AF=EM；

(2)、如图2，若AE平分∠BAF，求证：AF=BE＋DF.

查看试题解析
26. 如图，在平面直角坐标系中，直线AB：y＝ $\frac{1}{2}$ x＋m与x轴交于点A，与y轴交于点B（0，2），直线AC经过y轴负半轴上的点C，且OA＝OC.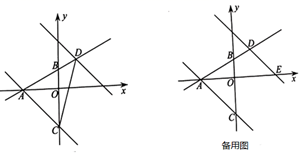

(1)、求直线AC的函数表达式；

(2)、直线AC向上平移9个单位，平移后的直线与直线AB交于点D，连结DC，求△ACD面积；

(3)、在（2）的条件下，平移后的直线与x轴交于点E，点M为直线AB上的一点，在平面直角坐标系中是否存在点N，使以点E，D，M，N为顶点的四边形是矩形，若存在，请直接写出点N的坐标；若不存在，请说明理由.

查看试题解析

分数	4	5	6	7	8	9	10
学生人数	1	a	3	4	b	2	3