浙江省杭州市江干区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列垃圾分类标识中，是中心对称图形的是（　　　）

A、 B、 C、 D、

查看试题解析
2. 二次根式 $\sqrt{2 - x}$ 有意义，则 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
3. 如果一个多边形的内角和等于540°，则它的边数为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 下列计算中正确的是（）

A、（﹣ $\sqrt{3}$ ）²＝﹣3 B、 $\sqrt{0.001}$ ＝0.1 C、 $\sqrt{1 \frac{1}{4}}$ ＝1 $\frac{1}{2}$ D、3 $\sqrt{\frac{1}{3}}$ ＝ $\sqrt{3}$

查看试题解析
5. 反比例函数的图象经过（﹣1，3）点，则这个反比例函数的表达式为（）

A、y＝﹣ $\frac{1}{3 x}$ B、y＝ $\frac{1}{3 x}$ C、y＝﹣ $\frac{3}{x}$ D、y＝ $\frac{3}{x}$

查看试题解析

6. 某市四家工厂2019年和2020年的生产总值如表（单位：万元），则设这四家工厂2019年和2020年的平均生产总值分别为

\bar{x_{1}}

，

\bar{x_{2}}

，则

\bar{x_{2}}

﹣

\bar{x_{1}}

的值为（）

单位	A厂	B厂	C厂	D厂
2019年	400	510	330	680
2020年	420	550	300	810

A、40 B、55 C、160 D、220

查看试题解析

7. 某公司计划用32m的材料沿墙（可利用）建造一个面积为120m²的仓库，设仓库中和墙平行的一边长为xm，则下列方程中正确的是（）

A、x（32﹣x）＝120 B、x（16﹣ $\frac{1}{2}$ x）＝120 C、x（32﹣2x）＝120 D、x（16﹣x）＝120

查看试题解析
8. 如图，四边形ABCD是菱形，点E、F分别在边BC、CD上，且BE＝DF，AB＝AE，若∠EAF＝75°，则∠C的度数为（）

A、85° B、90° C、95° D、105°

查看试题解析
9. 已知点A（x₁ ， y₁）在反比例函数y₁＝ $\frac{2 k}{x}$ 的图象上，点B（x₂ ， y₂）在一次函数y₂＝kx﹣k的图象上，当k＞0时，下列判断中正确的是（）

A、当x₁＝x₂＞2时，y₁＞y₂ B、当x₁＝x₂＜2时，y₁＞y₂ C、当y₁＝y₂＞k时，x₁＜x₂ D、当y₁＝y₂＜k时，x₁＞x₂

查看试题解析
10. 在一次活动课中，对如图所示的平行四边形（AD＞AB）进行折叠，第一次沿着AE折叠，点B落在点F处，接着两组同学分别尝试了两种不同的二次折叠，并给出了判断：组1：若沿着CF的中垂线折叠，则点D与点A必重合；组2：若沿着DF折叠，AD与DC所在的直线重合，且点A的对应点仍落在直线AF上，则 $\frac{S_{Δ A B F}}{S ▭_{C F A D}}$ ＝ $\frac{1}{3}$ （）

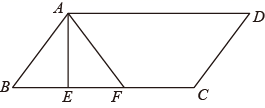A、组1判断正确，组2判断正确 B、组1判断正确，组2判断错误 C、组1判断错误，组2判断正确 D、组1判断错误，组2判断错误

查看试题解析

二、填空题

11. 平行四边形ABCD中，∠A＝40°，则∠D＝度

查看试题解析
12. 在一分钟跳绳测试中，甲、乙两班的平均成绩都为182个，方差S²_甲＝6.3，S²_乙＝5.5，成绩更为稳定的班级是.（填“甲”或“乙”）

查看试题解析
13. 如图，在矩形ABCD中，E，F分别是AB，AD的中点，若AC＝4，则EF的长是 .

查看试题解析
14. 若t是方程ax²+2x＝0（a≠0）的一个根，则 $Q = {(a t + 1)}^{2}$ 的值为 .

查看试题解析
15. 定义菱形的两条对角线长之比为“对角线比”.

(1)、若菱形成为正方形，则“对角线比”为；

(2)、当“对角线比”为4，菱形面积为800时，菱形的边长为 .

查看试题解析
16. 反比例函数y＝ $\frac{k}{x}$ ，当1≤x≤3时，函数y的最大值和最小值之差为4，则k＝.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{12}$ ﹣ $\sqrt{\frac{4}{3}}$ ；

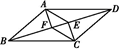
(2)、（2 $\sqrt{3}$ +3 $\sqrt{2}$ ）².

查看试题解析
18. 用指定的方法解方程：

(1)、（x﹣4）²＝2（x﹣4）（因式分解法）；

(2)、2x²﹣4x﹣1＝0（公式法）.

查看试题解析
19. 如图，在▱ABCD中，∠BAD和∠BCD的平分线AF，CE分别与对角线BD交于点F，E.
求证：四边形AFCE是平行四边形.

查看试题解析
20. 某学校从九年级同学中任意选取20人进行“引体向上”体能测试，前后进行了两次测试，第一次测试绘制成统计图，第二次测试绘制成统计表.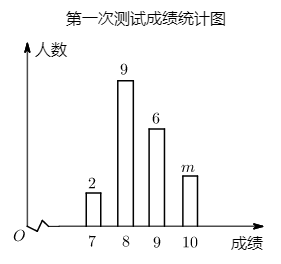

成绩

7

8

9

10

人数

1

5

10

4

(1)、m＝，第一次测试成绩的中位数是，第二次测试成绩的众数是；

(2)、请计算第一次测试的平均成绩；

(3)、若9分及以上为优秀，请计算两次测试中优秀人数增加的百分比（精确到0.1%）.

查看试题解析
21. 已知：如图，在正方形ABCD中，BD为对角线，E、F分别是AD，CD上的点，且AE＝CF，连接BE、BF、EF.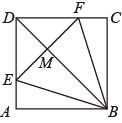

(1)、求证：EM＝FM；

(2)、若DE：AE＝2：1，设S_△ABE＝S，求S_△BEF（用含S的代数式表示）.

查看试题解析
22. 阅读材料：
已知：一次函数y＝﹣x+b与反比例函数y＝ $\frac{4}{x}$ （x＞0），当两个函数的图象有交点时，求b的取值范围.

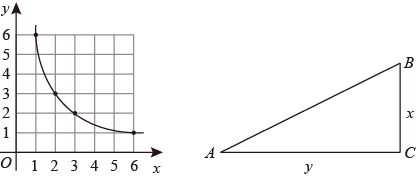(1)、方方给出了下列解答：
﹣x+b＝ $\frac{4}{x}$

x²﹣bx+4＝0

∵两个函数有交点

∴△＝b²﹣16≥0

但是方方遇到了困难：利用已学的知识无法解b²﹣16≥0这个不等式；

此时，圆圆提供了另一种解题思路；

第1步：先求出两个函数图象只有一个交点时，b＝ ▲ ；

第2步：画出只有一个交点时两函数的图象（请帮圆圆在直角坐标系中画出图象）；

第3步：通过平移y＝﹣x+b的图象，观察得出两个函数的图象有交点时b的取值范围是 ▲ .

应用：

如图，Rt△ABC中，∠C＝90°，BC的长为x，AC的长为y，且S_△ABC＝12.

(2)、求y关于x的函数表达式；

(3)、设x+y＝m，求m的取值范围.

查看试题解析
23. 如图，在矩形ABCD中，G为CD的中点，连接AG并延长交BC的延长线于点F，过G作EG⊥AF交直线BC于点E，连接AE.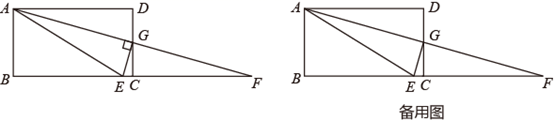

(1)、证明：∠DAG＝∠EAG；

(2)、设 $\frac{A D}{A B}$ ＝k（k＞0）
①若点E落在∠BAG的平分线上，求k的值.

②设m＝ $\frac{S_{Δ A B E}}{S_{Δ A D G}}$ ，求m关于k的函数表达式.

查看试题解析

成绩	7	8	9	10
人数	1	5	10	4