江苏省镇江市句容市、丹徒区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-27 类型：期末考试

进入出卷网下载

一、填空题

1. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是。

查看试题解析
2. 清明时节雨纷纷，这是.（选填“随机”或“必然” $)$ 事件.

查看试题解析
3. 反比例函数 $y = \frac{3 - m}{x}$ 的图象在第二、四象限，则m的取值范围是.

查看试题解析
4. 当x时，分式 $\frac{| x | - 3}{x - 3}$ 的值为零．

查看试题解析
5. 比较大小： $4 \sqrt{3}$ $3 \sqrt{5}$ ．

查看试题解析
6. 如图，正方形ABCD的边长为1，点E在BC的延长线上.如果BE=BD，那么CE=

查看试题解析
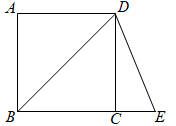7. 如图，在△ABC中，∠ACB＝90°，AB＝10cm，BC＝8cm，点D在边AB上，AD＝AC，AE⊥CD，垂足为E，点F是BC的中点，则EF＝cm.

查看试题解析
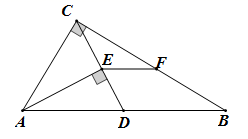8. 若 $a < \sqrt{5} < b$ ，且a、b是两个连续的整数，则 $\sqrt{\frac{a}{b}}$ =

查看试题解析
9. 在平面直角坐标系中，函数 $y = \frac{k}{x} (x > 0)$ 与 $y = x - 1$ 的图象交于点P(m，n)，且 $\frac{1}{n} - \frac{1}{m} = \frac{1}{4}$ ，则k的值为.

查看试题解析
10. 关于x的方程 $\frac{k}{2 x - 4} - 1 = \frac{x}{x - 2}$ 的解为正数，则k的取值范围是.

查看试题解析
11. 如图，在平面直角坐标系中，函数 $y = k x (k \neq 0)$ 与 $y = - \frac{1}{x}$ 的图象交于A、B两点，过点A作 $y$ 轴的垂线，交函数 $y = \frac{2}{x}$ 的图象于点C，连接BC，则△ABC的面积为.

查看试题解析
12. 已知实数m、n满足 $m^{2} + 2 m - 2 = 0 ， m - n = 2$ ，则代数式 $\frac{1}{m + 1} + \frac{2}{n} =$ .

查看试题解析

二、单选题

13. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
14. 不列调查方式中，最合适的是（）

A、调查某品牌电脑的使用寿命，采用普查的方式 B、调查游客对镇江金山景区的满意程度情况，采用抽样调查的方式 C、调查“天问一号”火星探测器零部件质量情况，采用抽样调查的方式 D、调查镇江地区初中学生的睡眠时间，采用普查的方式

查看试题解析
15. 将分式 $\frac{x - y}{x + 2 y}$ 中 $x$ 、 $y$ 的值都变为原来的2倍，则该分式的值（）

A、变为原来的2倍 B、变为原来的4倍 C、不变 D、变为原来的一半

查看试题解析
16. 若O是四边形ABCD对角线的交点且OA=OB=OC=OD，则四边形ABCD是（）

A、平行四边形 B、矩形 C、正方形 D、菱形

查看试题解析
17. 对于实数 $a$ ， $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{2}{a - b^{2}}$ ，这里等式右边是通常的实数运算.例如： $1 \otimes 3 = \frac{2}{1 - 3^{2}} = - \frac{1}{4}$ ，则方程 $x \otimes (- 1) = \frac{6}{x - 1} - 1$ 的解是（）

A、 $x = 4$ B、 $x = 5$ C、 $x = 6$ D、 $x = 7$

查看试题解析
18. 如图，一次函数 $y = \frac{1}{5} x - 1$ 与x轴、y轴的交点分别为A、B，△ABC是以AB为斜边的等腰直角三角形，其中，直角顶点C在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上，则k的值是（）

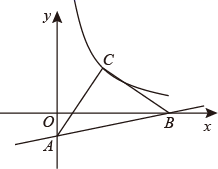A、4 B、6 C、8 D、9

查看试题解析
19. 如图，以Rt△ABC的斜边BC为边，在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO.若AB＝2，AO＝ $3 \sqrt{2}$ ，则AC的长等于（）

A、 $12 \sqrt{2}$ B、8 C、 $4 + 3 \sqrt{2}$ D、 $2 + 3 \sqrt{2}$

查看试题解析

三、解答题

20. 计算

(1)、 $\sqrt{18} \times \sqrt{3} \div \sqrt{2}$

(2)、 $2 \sqrt{20} － \sqrt{5} + 5 \sqrt{\frac{1}{5}}$

(3)、 $(3 + \sqrt{2}) (3 － \sqrt{2}) － {(1 + \sqrt{2})}^{2}$

查看试题解析
21.

(1)、先化简 $(1 + \frac{1}{x - 1}) \div$ $\frac{x}{x^{2} - 1}$ ，再选择一个恰当的x值代入并求值.

(2)、解方程： $\frac{1 - x}{x - 2}$ ＝ $\frac{1}{2 - x} - 2$ .

查看试题解析
22. 4月23日是世界读书日，学校学生发展中心在全校随机抽取了一部分学生，对他们喜欢读的书进行统计，共归为四类： A：历史类、B：文学类、C：科普类、D：艺术类，绘制出了两幅不完整的统计图，请你根据图中信息解答下列问题：

(1)、共抽取了名学生进行调查；

(2)、将图甲中的折线统计图补充完整；

(3)、图乙中B类所占圆心角的度数为；

(4)、若该校有3000名学生，请你估计选择“A：历史类”的学生约有名.

查看试题解析
23. 如图，在矩形ABCD中，点O为对角线AC的中点，过点O作 $E F ⊥ A C$ 交BC于点E，交AD于点F，连接AE，CF.

(1)、求证：四边形AECF是菱形；

(2)、连接OB，若 $A B = 4$ ， $A F = 5$ ，求OB的长.

查看试题解析
24. 已知一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x} (x > 0)$ 的图象交于点A，与x轴交于点B(5，0)，若OB=AB，且 $S_{Δ O A B} = \frac{15}{2}$ .

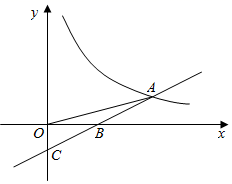(1)、求反比例函数与一次函数的表达式；

(2)、直接写出当 $x > 0$ 时，不等式 $\frac{m}{x} > k x + b$ 的解集；

(3)、若点P在y轴上，Q在反比例函数 $y = \frac{m}{x} (x > 0)$ 的图象上，且四边形ABPQ恰好是平行四边形，直接写出此时点P的坐标.

查看试题解析
25. 列方程解应用题
甲、乙两人加工同一种服装，乙每天比甲多加工一件，乙加工服装24件所用的时间与甲加工服装20件所用时间相同，求甲每天加工服装多少件.

查看试题解析
26. 在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x}$ （x＞0）的图象G与直线l： $y = x - 1$ 交于点A（m，2）.

(1)、求k的值；

(2)、已知点P（n，0）（n＞0），过点P作平行于y轴的直线，与图象G交于点B，与直线l交于点C.我们规定：横、纵坐标都是整数的点叫做整点.记图象G在点A、B之间的部分与线段AC、BC围成的区域（不含边界）为W区域.
①当n＝5时，W区域内的整点的坐标是；

②若W区域内的整点恰好为6个，则n的取值范围为.

查看试题解析
27. 如图，将矩形ABCD绕点顺A时针旋转α°(0°＜α＜360°)，得到矩形AEFG.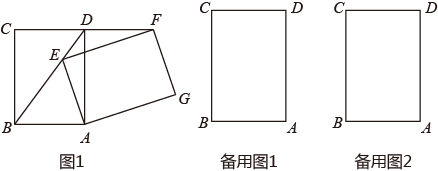

(1)、如图1.当点E在BD上时，
①求证：∠BEA=∠BDC；

②连接AF，判断四边形BAFD的形状，并说明理由

(2)、若AB=4，AD= $3 \sqrt{3}$ ，当GC＝GB时，求ED的长度（画出图形，直接写出结果）

查看试题解析