江苏省扬州市江都区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列是一组logo设计的图片，其中不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，必然事件是（）

A、打开电视，正在播新闻 B、明天将下雨 C、小华家买彩票将会获奖 D、13个小朋友中至少有2人的出生月份相同

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = 6$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$

查看试题解析
4. 对于分式 $\frac{1}{x - 3}$ ，变形正确的是（）

A、 $\frac{1}{x + 3}$ B、 $\frac{1}{3 - x}$ C、 $- \frac{1}{x + 3}$ D、 $- \frac{1}{3 - x}$

查看试题解析
5. 某学校课外活动小组为了解同学们喜爱的电影类型，设计了如下的调查问卷（不完整）：

准备在“①国产片，②科幻片，③动作片，④喜剧片，⑤亿元大片”中选取三个作为该问题的备选答案，选取合理的是（）

A、①②③ B、①③⑤ C、②③④ D、②④⑤

查看试题解析
6. 如图，在平行四边形ABCD中，AB＝4，BC＝6，按以下步骤作图：①以点C为圆心，适当长为半径作弧，分别交BC，CD于M，N两点；②分别以点M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径作弧，两弧在平行四边形ABCD的内部交于点P；③连接CP并延长交AD于点E，交BA的延长线于点F，则AF的长为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 下列关于反比例函数 $y = - \frac{2}{x}$ ，说法不正确的是（）

A、点(－2，1)、(－1，2)均在其图象上 B、双曲线分布在二、四象限 C、该函数图象上有两点A $(x_{1} ， y_{1})$ 、B $(x_{2} ， y_{2})$ ，若 $x_{1}$ < $x_{2}$ ，则 $y_{1}$ < $y_{2}$ D、当 $y < - 2$ 时，x的范围是0 < x < 1

查看试题解析
8. 如图，在平面直角坐标系中，A(8，0)，点B为一次函数 $y = x$ 图象上的动点，以OB为边作正方形OBCD，当AB最小时，点D恰好落在反比例函数 $y = \frac{k}{x}$ 的图象上，则 $k =$ （）

A、-9 B、-12 C、-16 D、-25

查看试题解析

二、填空题

9. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 如图，A，B两点被池塘隔开，不能直接测量其距离.于是小明在岸边选一点C，连接CA，CB，分别延长到点M，N，使AM=AC，BN=BC，测得MN=20m，则A，B间的距离为m.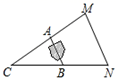

查看试题解析
11. 在一个不透明的袋中装有除颜色外其余均相同的 $n$ 个小球，其中有6个黑球，从袋中随机摸出一球，记下其颜色，称为一次摸球试验，之后把它放回袋中，搅匀后，再继续摸出一球，利用计算机模拟的结果，摸出黑球的频率在0.5附近波动，由此可以估计出 $n$ 的值是.

查看试题解析
12. 请写出一个与 $\sqrt{\frac{1}{5}}$ 为同类二次根式的最简二次根式.

查看试题解析
13. 如图，在平面直角坐标系中，每个小正方形边长均为1，将 $△$ ABC绕P点逆时针旋转至 $△ A^{'} B^{'} C^{'}$ ，使点B′恰好落在y轴上，则旋转中心P的坐标是.

查看试题解析
14. 如图，已知点A是反比例函数 $y = - \frac{3}{x}$ ( $x < 0$ )的图象上的一个动点，连接OA，若将线段OA绕点O顺时针旋转90°得到线段OB，则点B所在反比例图象的函数关系式是.

查看试题解析
15. 设函数 $y = \frac{1}{x}$ 与y=x﹣1的图象的交点坐标为（a，b），则 $\frac{1}{a} - \frac{1}{b}$ 的值为.

查看试题解析
16. 若关于x的分式方程 $\frac{3 x}{x - 2}$ ＝ $\frac{m}{2 - x}$ +5的解为正数，则m的取值范围为.

查看试题解析
17. 我们知道：四边形具有不稳定性.如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点 $D^{'}$ 处，点E为x轴上一动点，当 $E D' + E C'$ 取最小值时，点E的坐标为.

查看试题解析

三、解答题

18. 一次函数y=-x+1与反比例函数

y = \frac{k}{x}

(k＜0)中，x与y的部分对应值如下表：

x	-3	-2	-1	1	2	3
y=-x+1	4	3	2	0	-1	-2
$y = \frac{k}{x}$	$\frac{2}{3}$	1	2	-2	-1	- $\frac{2}{3}$

则不等式 $\frac{k}{x} + x - 1$ ＞0的解集为.

查看试题解析

19. 计算：

(1)、 $(2 \sqrt{6} + \sqrt{\frac{2}{3}}) \times \sqrt{3} - \sqrt{32}$

(2)、已知 $x = \sqrt[]{3} + 1$ ，求代数式 $x^{2} - 2 x$ 的值.

查看试题解析
20. 化简式子 $\frac{x^{2} - 2 x}{x^{2}} \div$ （x $- \frac{4 x - 4}{x}$ ），从0、1、2中取一个合适的数作为x的值代入求值．

查看试题解析

21. 某校团委组织了一次全校1000名学生参加的环保知识竞赛，并设优胜奖.赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解环保知识竞赛的成绩，随机抽取了其中100名学生的成绩（成绩x取整数，总分100分）进行整理，得到下列不完整的统计图表：

成绩x/分	频数	频率
50≤x＜60	10	0.10
60≤x＜70	25	0.25
70≤x＜80	30	b
80≤x＜90	a	0.20
90≤x≤100	15	0.15

请根据所给信息，解答下列问题：

(1)、a= ， b=；

(2)、请补全频数分布直方图；

(3)、这次抽样调查的样本是；

(4)、若这次比赛成绩在80分以上（含80分）的学生获得优胜奖，则该校参加这次比赛的1000名学生中获优胜奖的约有人.

查看试题解析

22. 用※定义一种新运算：对于任意实数m和n，规定m※n $= m^{2} n - m n - 3 n$ ，如：1※2 $= 1^{2} \times 2 - 1 \times 2 - 3 \times 2 = - 6$ .

(1)、求（﹣2）※ $\sqrt{3}$ ；

(2)、若3※m＜－6，化简 $\sqrt{（ 2 - m)^{2}} + {(\sqrt{- m - 2})}^{2}$ .

查看试题解析
23. 已知：如图， $△$ ABC为锐角三角形，AB>AC.
求作：BC边上的高AD.

作法：①以点A为圆心，AB长为半径画弧，交BC的延长线于点E；

②分别以点B，E为圆心，以AB长为半径画弧，两弧相交于点F(不与点A重合)；

③连接AF交BC于点D.

线段AD就是所求作的线段.

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明.
证明：连接AE，EF，BF.

∵AB=AE= EF = BF，

∴四边形ABFE是（）（填推理依据）.

∴AF⊥BE（）（填推理依据）.

即AD是 $△$ ABC中BC边上的高.

查看试题解析
24. 八年级（1）班开展“诵读经典，光亮人生”读书活动，小智和小慧同学读了同一本480页的名著.小智每天读的页数是小慧每天读的页数的1.2倍，小慧读完这本书比小智多用4天.求小慧每天读这本名著的页数.

查看试题解析
25. 如图，矩形ABCD中，点P是线段AD上的一个动点，O为BD的中点，PO的延长线交BC于Q.

(1)、求证：OP＝OQ；

(2)、若AD＝8cm，AB＝6cm，点P从点A出发，以1cm/s的速度向点D运动（不与D重合）.设点P运动的时间为t秒，当t为何值时，四边形PBQD是菱形？

查看试题解析
26. 阅读材料，并回答问题：
小亮在学习分式过程中，发现可以运用“类比”的方法，达成事半功倍的学习效果，比如学习异分母分式加减可以类比异分母分数的加减，先通分，转化为同分母分式加减进行运算，解分式方程可以类比有分母的一元一次方程，先去分母，转化为整式方程求解；比较分式的大小，可以类比整式比较大小运用的“比差法”……

问题：

(1)、材料中分式“通分”的依据是；“将分式方程转化为整式方程”的“去分母”的依据是；

(2)、类比解分式方程的思想方法，解方程： $\sqrt{1 - 2 x} = 3$ ；

(3)、数学家斐波那契编写的《算经》中有如下问题：甲、乙两组人各自平分钱，已知两组人数相同，相关信息如表：

组别

人数（人）

总金额（元）

甲

$b^{2}$

乙

$2 b - 5$

试比较甲乙两组哪组人均分的钱多？

查看试题解析
27. 如图，正方形ABCD的边长为1，点P为边BC上任意一点（可与B点或C点重合），分别过B、C、D作射线AP的垂线，垂足分别是 $B^{'} ， C^{'} ， D^{'}$ .

(1)、求证： $D D^{'} = A B^{'}$ ；

(2)、设 $A P = x ， B B^{'} + C C^{'} + D D^{'} = y$ ，求y与x的函数关系式；

(3)、直接写出y的最大值为，最小值为.

查看试题解析
28. 我们已经学习了正比例函数 $y = k x$ 和反比例函数 $y = \frac{m}{x}$ 的图象和性质，下面，我们研究函数 $y = k x + \frac{m}{x}$ 的图象和性质，我们不妨特殊化，设 $k = 1$ ， $m = 1$ ，即 $y = x + \frac{1}{x}$ .

(1)、① 函数 $y = x + \frac{1}{x}$ 的自变量x的取值范围是 ▲ ；
②容易发现，当 $x > 0$ 时， $y > 0$ ；当 $x < 0$ 时， $y < 0$ .由此可见，图象在第 ▲ 象限；

③阅读材料：当 $x > 0$ 时， $y = x + \frac{1}{x} = {(\sqrt{x})}^{2} + {(\frac{1}{\sqrt{x}})}^{2} = {(\sqrt{x} - \frac{1}{\sqrt{x}})}^{2} + 2 \geq 2$ .当 $\sqrt{x} = \frac{1}{\sqrt{x}}$ 时，即 $x = 1$ ， $y$ 有最小值是2.请仿照上述过程，求出当 $x < 0$ 时， $y$ 的最大值；

(2)、为了画函数 $y = x + \frac{1}{x}$ 的图象，小明通过列表，描点画出了下图，请连线；

(3)、观察图象，当 $y$ 随着 $x$ 的增大而增大时，自变量x的取值范围是；

(4)、某隧道长185m，一个匀速前进的车队有10辆车，每辆车长4m，相邻两车的距离d（m）与车速v（m/s）的关系式为 $d = \frac{1}{9} v^{2}$ ，求自第1辆车车头进隧道至第10辆车车尾出隧道所用时间的最小值.

查看试题解析

组别	人数（人）	总金额（元）
甲		$b^{2}$
乙		$2 b - 5$