江苏省苏州市姑苏区六校2020-2021学年八年级下学期数学期末联考试卷
试卷更新日期:2021-07-27 类型:期末考试
一、单选题
-
1. 苏州市区今年共有25000名考生参加中考,为了了解这25000名考生的体育成绩,从中抽取了1000名考生的体育成绩进行统计分析,以下说法正确的是( )A、该调查方式是普查 B、25000名考生是总体 C、1000名考生的体育成绩是总体的一个样本 D、样本容量是1000名考生2. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,摸到黑球是( )A、必然事件 B、随机事件 C、不可能事件 D、以上事件都有可能4. 若代数式 有意义,则 的取值范围是( )A、 B、 C、 D、5. 若 ,则 的值为( )A、 B、 C、 D、6. 下列根式中,最简二次根式的是( )A、 B、 C、 D、7. 若关于x的分式方程 有正整数解,则整数m为( )A、-3 B、0 C、-1 D、-1或08. 反比例函数 的图象如图所示,当 时, 的取值范围是( )
3. 一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,摸到黑球是( )A、必然事件 B、随机事件 C、不可能事件 D、以上事件都有可能4. 若代数式 有意义,则 的取值范围是( )A、 B、 C、 D、5. 若 ,则 的值为( )A、 B、 C、 D、6. 下列根式中,最简二次根式的是( )A、 B、 C、 D、7. 若关于x的分式方程 有正整数解,则整数m为( )A、-3 B、0 C、-1 D、-1或08. 反比例函数 的图象如图所示,当 时, 的取值范围是( )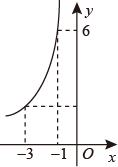 A、 B、 C、 D、9. 如图,在正方形网格中: 、 的顶点都在正方形网格的格点上, ,则 的度数为( )
A、 B、 C、 D、9. 如图,在正方形网格中: 、 的顶点都在正方形网格的格点上, ,则 的度数为( ) A、30° B、45° C、60° D、75°10. 如图,在矩形 中,将 绕点 逆时针旋转90°得到 , 、 、 三点恰好在同一直线上, 与 相交于点 ,连接 .以下结论正确的是( )
A、30° B、45° C、60° D、75°10. 如图,在矩形 中,将 绕点 逆时针旋转90°得到 , 、 、 三点恰好在同一直线上, 与 相交于点 ,连接 .以下结论正确的是( )
① :② ;③点 是线段 的黄金分割点;④
A、①② B、①③ C、①②③ D、①③④二、填空题
-
11. 当 时,分式 的值为零.12. 若点 , 在同一个反比例函数的图象上,则 的值为.13. 小兰身高 ,她站立在阳光下的影子长为 ;她把手臂竖直举起,此时影子长为 ,那么小兰的手臂超出头顶cm.14. 如图, 是 的中线,点 、 、 分别是 、 、 的中点,连接 、 .现随机向 内掷一枚小针,则针尖落在阴影区域的概率是.
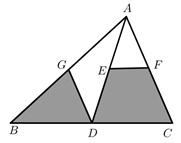 15. 如图, ,若 , ,则 .
15. 如图, ,若 , ,则 . 16. 如图, 中, 、 分别为 , 上的点,已知 ,且 的面积是3,则 的面积是.
16. 如图, 中, 、 分别为 , 上的点,已知 ,且 的面积是3,则 的面积是.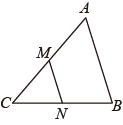 17. 如图,在□ABCD中,∠A=75° , 将□ABCD绕顶点B顺时针旋转到□A1BC1D1 , 当C1D1首次经过顶点C时,旋转角∠ABA1=.
17. 如图,在□ABCD中,∠A=75° , 将□ABCD绕顶点B顺时针旋转到□A1BC1D1 , 当C1D1首次经过顶点C时,旋转角∠ABA1=.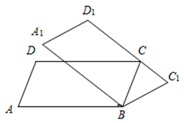 18. 如图,菱形 的边长为 , ,点 是 边上任意一点(可以与点 或点 重合), 分别过点 、 、 作射线 的垂线,垂足分别是 、 、 ,设 ,则 的取值范围是.
18. 如图,菱形 的边长为 , ,点 是 边上任意一点(可以与点 或点 重合), 分别过点 、 、 作射线 的垂线,垂足分别是 、 、 ,设 ,则 的取值范围是.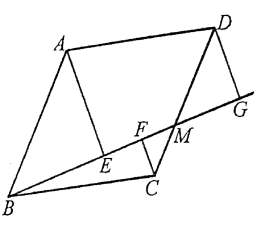
三、解答题
-
19. 计算:20. 解分式方程:21. 先化简,再求值 ,其中 .22. 6月中下旬正是苏州东山特色水果——“乌紫杨梅”成熟的时候.某水果店第一次用1080元购进一批乌紫杨梅,由于销售情况良好,该店又用2400元购进一批乌紫杨梅,所购数量是第一次购进数量的2倍,但进货价每千克涨了4元.问:第一次所购乌紫杨梅的进货价是每千克多少元?23. 如图,在边长为1的小正方形组成的网格中, 的顶点在格点(网格线的交点)上,以点 为原点建立平面直角坐标系,点 的坐标为(1,0).
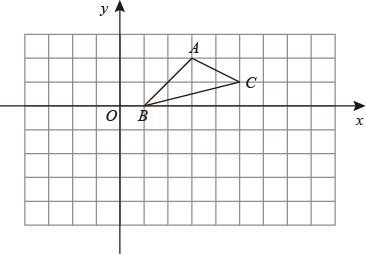
( 1 )将 向左平移5个单位长度,得到 ,画出 ;
( 2 )以点 为位似中心,将 放大到两倍(即新图与原图的相似比为2),得到 ,在所给的方格纸中画出 ;
( 3 )若点 是 的中点,经过(1)、(2)两次变换, 的对应点 的坐标是 .
24. 某校组织学生开展了为贫困山区孩子捐款活动,随机抽查了部分同学捐款的情况进行统计,并对获取的数据进行了整理,根据整理结果,绘制了如图所示的两幅不完整的统计图,请根据所提供的信息,解答下列问题: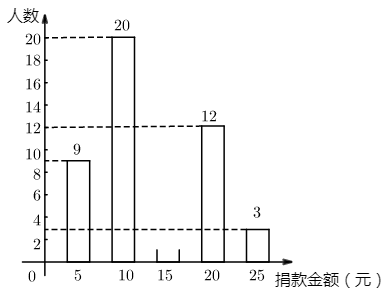
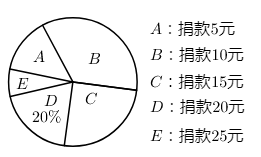 (1)、本次共抽查学生 ▲ 人,并将条形统计图补充完整;(2)、扇形统计图中, 对应的圆心角是.(3)、全校1200名学生中,捐款20元及以上的学生估计有多少人?25. 如图,直线 与 轴、 轴分别相交于点 、点 ,以线段 为边在第一象限作正方形 .反比例函数 在第一象限内的图象经过点 .
(1)、本次共抽查学生 ▲ 人,并将条形统计图补充完整;(2)、扇形统计图中, 对应的圆心角是.(3)、全校1200名学生中,捐款20元及以上的学生估计有多少人?25. 如图,直线 与 轴、 轴分别相交于点 、点 ,以线段 为边在第一象限作正方形 .反比例函数 在第一象限内的图象经过点 .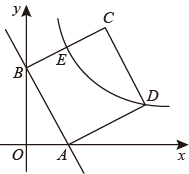 (1)、求反比例函数的解析式;(2)、将正方形 沿 轴向上平移几个单位能使点 落在(1)中所得的双曲线上?26. 如图,在 中, ,点P是边 上的一个动点,过点P作 交 于点Q,点D为线段 的中点,且 平分 .
(1)、求反比例函数的解析式;(2)、将正方形 沿 轴向上平移几个单位能使点 落在(1)中所得的双曲线上?26. 如图,在 中, ,点P是边 上的一个动点,过点P作 交 于点Q,点D为线段 的中点,且 平分 . (1)、求证: ;(2)、若 , ,求 的长.27. 如图,在 中,点 是 的中点,点 是线段 的延长线上的一点,连接 ,过点 作CD∥AB,与线段 的延长线交于点 ,连接 、 .
(1)、求证: ;(2)、若 , ,求 的长.27. 如图,在 中,点 是 的中点,点 是线段 的延长线上的一点,连接 ,过点 作CD∥AB,与线段 的延长线交于点 ,连接 、 . (1)、求证:四边形 是平行四边形.(2)、若 , :
(1)、求证:四边形 是平行四边形.(2)、若 , :①当四边形 是矩形时,求 的长;
②当BE= ▲ 时,四边形 是菱形.(请直接写出答案)
28. 已知矩形 中, , ,点 是边 的中点.(1)、如图,连接 并延长,与 的延长线交干点 ,问:线段 上是否存在点 ,使得 为等腰三角形,若存在,请求出 的长,若不存在,请说明理由.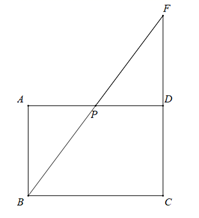 (2)、如图,把矩形 沿直线 折益,使点 落在点 上,直线 与 、 、 的交点分别为 、 、 ,求折痕 的长.
(2)、如图,把矩形 沿直线 折益,使点 落在点 上,直线 与 、 、 的交点分别为 、 、 ,求折痕 的长. (3)、如图:在(2)的条件下,以点 为原点、分别以矩形 的两条边 、 所在的直线为 轴和 轴建立平面直角坐标系,若点 在 轴上,在平面内是否存在点 ,使以 、 、 、 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(3)、如图:在(2)的条件下,以点 为原点、分别以矩形 的两条边 、 所在的直线为 轴和 轴建立平面直角坐标系,若点 在 轴上,在平面内是否存在点 ,使以 、 、 、 为顶点的四边形是菱形?若存在,请直接写出点 的坐标;若不存在,请说明理由.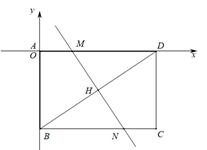 (4)、如图:若点 为 边上的一个动点,连结 ,以 为边向下方作等边 ,连结 ,则 的最小值是.(请直接写出答案)
(4)、如图:若点 为 边上的一个动点,连结 ,以 为边向下方作等边 ,连结 ,则 的最小值是.(请直接写出答案)