江苏省苏州市高新区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-27 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列式子,属于最简二次根式的是( )A、 B、 C、 D、3. 若菱形的两条对角线的长分别为6和10,则菱形的面积为( )A、15 B、24 C、30 D、604. 如果把分式 中的x和y都扩大为原来的2倍,那么分式的值( )A、扩大为原来的4倍 B、扩大为原来的2倍 C、不变 D、缩小为原来的 倍5. 如图,在▱ABCD中,AE平分∠BAD,交CD边于E,AD=6,EC=4,则AB的长为( )
2. 下列式子,属于最简二次根式的是( )A、 B、 C、 D、3. 若菱形的两条对角线的长分别为6和10,则菱形的面积为( )A、15 B、24 C、30 D、604. 如果把分式 中的x和y都扩大为原来的2倍,那么分式的值( )A、扩大为原来的4倍 B、扩大为原来的2倍 C、不变 D、缩小为原来的 倍5. 如图,在▱ABCD中,AE平分∠BAD,交CD边于E,AD=6,EC=4,则AB的长为( )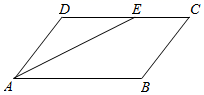 A、10 B、6 C、4 D、246. 如图,A、B两地被池塘隔开,小强通过下面的方法估测出A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点D、E,并且步测出DE长,由此推算出AB长.若步测DE的长为50m,则A、B间的距离是( )
A、10 B、6 C、4 D、246. 如图,A、B两地被池塘隔开,小强通过下面的方法估测出A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点D、E,并且步测出DE长,由此推算出AB长.若步测DE的长为50m,则A、B间的距离是( )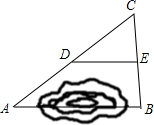 A、25m B、50m C、75m D、100m7. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 (k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A、25m B、50m C、75m D、100m7. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 (k≠0)的一部分,则当x = 16时,大棚内的温度约为( )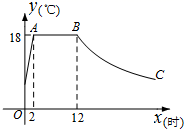 A、18℃ B、15.5℃ C、13.5℃ D、12℃8. 三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长为( )A、12 B、14 C、12或14 D、249. 已知一组数据:1,2,a,b,5,8的平均数和中位数都是4(a,b均为正整数,在去掉其中的一个最大数后,该组数据的( )A、中位数不变 B、众数不变 C、平均数不变 D、方差不变10. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )
A、18℃ B、15.5℃ C、13.5℃ D、12℃8. 三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长为( )A、12 B、14 C、12或14 D、249. 已知一组数据:1,2,a,b,5,8的平均数和中位数都是4(a,b均为正整数,在去掉其中的一个最大数后,该组数据的( )A、中位数不变 B、众数不变 C、平均数不变 D、方差不变10. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )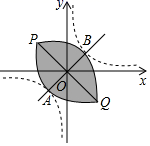 A、 B、 C、2 D、4
A、 B、 C、2 D、4二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 为了践行“首都市民卫生健康公约”,某班级举办“七步洗手法”比赛活动,小明的单项成绩如表所示(各项成绩均按百分制计):
项目
书面测试
实际操作
宣传展示
成绩(分)
96
98
96
若按书面测试占30%、实际操作占50%、宣传展示占20%,计算参赛个人的综合成绩(百分制),则小明的最后得分是.
13. 已知点P(a,b)是反比例函数 图象上异于点(-1,-1)的一个动点,则 =.14. 如果m是方程x2-2x-6=0的一个根,那么代数式2m-m2+7的值为 .15. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是.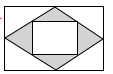 16. 如图,直线y=2x与双曲线 交于A(m,4)、B两点,则不等式 的解集为.
16. 如图,直线y=2x与双曲线 交于A(m,4)、B两点,则不等式 的解集为.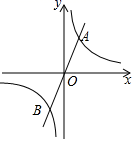 17. 数学家莫伦在1925年发现了世界上第一个完美长方形(如图1),即它恰好能被分割成10个大小不同的正方形,从这以后人们开始热衷图形完美分割的研究,▱EFGH被分割成13个小正三角形(如图2),已知中间最小的两个正三角形△ABC和△ADC边长均为2,▱EFGH的周长为.
17. 数学家莫伦在1925年发现了世界上第一个完美长方形(如图1),即它恰好能被分割成10个大小不同的正方形,从这以后人们开始热衷图形完美分割的研究,▱EFGH被分割成13个小正三角形(如图2),已知中间最小的两个正三角形△ABC和△ADC边长均为2,▱EFGH的周长为.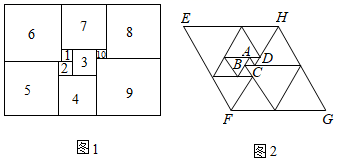 18. 如图,菱形ABCD的边长为 ,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为.
18. 如图,菱形ABCD的边长为 ,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为.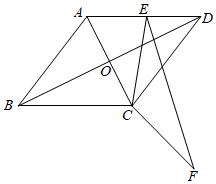
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中 .21. 解方程:(1)、(2)、22. 某市为了解初中生每周阅读课外书籍时长(单位:小时)的情况,在全市范围内随机抽取了n名初中生进行调查,并将所收集的数据分组整理,绘制了如图所示的不完整的频数分布直方图和扇形统计图.
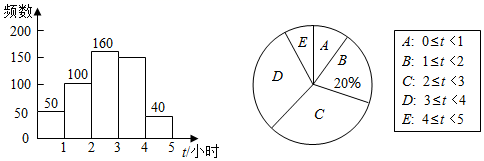
根据图中信息,解答下列问题:
(1)、在这次调查活动中,采取的调查方式是(填写“全面调查”或“抽样调查”),n=;(2)、若该市有15000名初中生,请你估计该市每周阅读课外书籍时长在“4≤t<5”范围的初中生有多少名?23. 热情的刘老师邀请两位朋友小高和小新来苏州游玩,他向两人推荐了四个游览地:苏州乐园、太湖湿地公园、白马涧龙池景区和淮海街,并做成四个外形完全一致的纸签让两位朋友随机抽取.(1)、若小高先抽中了“苏州乐园”(不放回),则小新再抽签时选择“太湖湿地公园”的概率是 :(2)、若小高先抽签后立即放回,再由小新抽签,求两人抽取到同一个景点的概率.24. 如图,矩形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.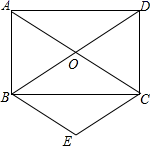 (1)、求证:四边形OBEC是菱形;(2)、若AD=4,AB=2,求菱形OBEC的面积.25. 苏州某工厂生产一批小家电,2019年的出厂价是144元,2020年、2021年连续两年改进技术降低成本,2021年出厂价调整为100元.(1)、这两年出厂价下降的百分比相同,求平均下降的百分率(精确到0.01%).(2)、某商场今年销售这批小家电的售价为140元时,平均每天可销售20台,为了减少库存,商场决定降价销售,经调查发现小家电单价每降低5元,每天可多售出10台,如果每天盈利1250元,销售单价应为多少元?26. 如图,过点A(0,-2),B(-4,0)的直线与反比例函数 的图象交于点C(-6,a),点N在反比例函数 的图象上,且在点C的右侧,过点N作y轴的平行线交直线AB于点Q.
(1)、求证:四边形OBEC是菱形;(2)、若AD=4,AB=2,求菱形OBEC的面积.25. 苏州某工厂生产一批小家电,2019年的出厂价是144元,2020年、2021年连续两年改进技术降低成本,2021年出厂价调整为100元.(1)、这两年出厂价下降的百分比相同,求平均下降的百分率(精确到0.01%).(2)、某商场今年销售这批小家电的售价为140元时,平均每天可销售20台,为了减少库存,商场决定降价销售,经调查发现小家电单价每降低5元,每天可多售出10台,如果每天盈利1250元,销售单价应为多少元?26. 如图,过点A(0,-2),B(-4,0)的直线与反比例函数 的图象交于点C(-6,a),点N在反比例函数 的图象上,且在点C的右侧,过点N作y轴的平行线交直线AB于点Q.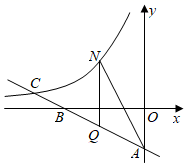 (1)、求直线AB和反比例函数的表达式;(2)、若△ANQ面积为 ,求点N的坐标.27. 动点P在□ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知P的速度为1个单位长度/s,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图2所示.
(1)、求直线AB和反比例函数的表达式;(2)、若△ANQ面积为 ,求点N的坐标.27. 动点P在□ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知P的速度为1个单位长度/s,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图2所示.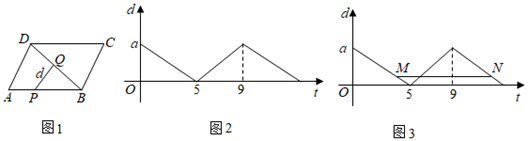 (1)、若a=3,求当t=8时△BPQ的面积;(2)、如图3,点M,N分别在函数第一和第三段图象上,线段MN平行于横轴,M、N的横坐标分别为t1、t2 , 设t1、t2时点P走过的路程分别为 ,若 = 16,求t1、t2的值.28. 定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线 ,点A,D在直线 上,点B,C在直 上,若∠BAD=2∠BCD,则四边形ABCD是半对角四边形.
(1)、若a=3,求当t=8时△BPQ的面积;(2)、如图3,点M,N分别在函数第一和第三段图象上,线段MN平行于横轴,M、N的横坐标分别为t1、t2 , 设t1、t2时点P走过的路程分别为 ,若 = 16,求t1、t2的值.28. 定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线 ,点A,D在直线 上,点B,C在直 上,若∠BAD=2∠BCD,则四边形ABCD是半对角四边形.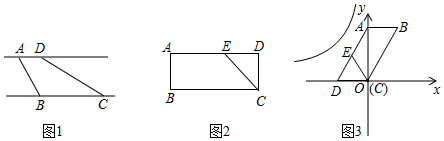 (1)、如图2,点E是矩形ABCD的边AD上一点,AB=1,AE=2.若四边形ABCE为半对角四边形,求AD的长:(2)、如图3,以▱ABCD的顶点C为坐标原点,边CD所在直线为x轴,对角线AC所在直线为y轴,建立平面直角坐标系.点E是边AD上一点,满足BC=AE+CE.求证:四边形ABCE是半对角四边形;(3)、在(2)的条件下,当AB=AE= ,∠B=60°时,将四边形ABCE向左平移a(a>0)个单位后,恰有两个顶点落在反比例函数 的图象上,求k的值.
(1)、如图2,点E是矩形ABCD的边AD上一点,AB=1,AE=2.若四边形ABCE为半对角四边形,求AD的长:(2)、如图3,以▱ABCD的顶点C为坐标原点,边CD所在直线为x轴,对角线AC所在直线为y轴,建立平面直角坐标系.点E是边AD上一点,满足BC=AE+CE.求证:四边形ABCE是半对角四边形;(3)、在(2)的条件下,当AB=AE= ,∠B=60°时,将四边形ABCE向左平移a(a>0)个单位后,恰有两个顶点落在反比例函数 的图象上,求k的值.