江苏省南京市鼓楼区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-27 类型:期末考试
一、单选题
-
1. 为了解某市5.4万名考生的中考数学成绩,从中抽出2000名考生的数学成绩进行调查,抽出的2000名考生的数学成绩是( )A、样本容量 B、总体 C、个体 D、样本2. 中国古代的铜锁制作都十分精美,下面的四把锁中,从形状上看是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果把分式 中的 , 都扩大为原来的6倍,那么分式的值( )A、不变 B、是原来的6倍 C、是原来的 D、是原来的4. 下列式子为最简二次根式的是( )A、 B、 C、 D、5. 用配方法将 变形,结果是( )A、 B、 C、 D、6. 如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( )
3. 如果把分式 中的 , 都扩大为原来的6倍,那么分式的值( )A、不变 B、是原来的6倍 C、是原来的 D、是原来的4. 下列式子为最简二次根式的是( )A、 B、 C、 D、5. 用配方法将 变形,结果是( )A、 B、 C、 D、6. 如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( ) A、7个 B、8个 C、9个 D、10个
A、7个 B、8个 C、9个 D、10个二、填空题
-
7. 计算 的结果是.8. 若分式 的值为0,则x的值是.9. 不透明的袋子中有除颜色外完全相同的4个红球和2个绿球,从袋子中随机摸出3个球,至少有1个红球是.(填“随机事件”,“必然事件”或“不可能事件”)10. 设 , 是关于 的方程 的两个根,且 ,则 .11. 某同学要统计本校图书馆最受学生欢迎的图书种类,以下是打乱顺序的统计步骤:
①从扇形图中分析出最受学生欢迎的种类;②去图书馆收集学生借阅图书的记录;③绘制扇形图来表示各个种类所占的百分比;④整理借阅图书记录并绘制频数分布表,正确统计步骤的顺序是 .
12. 若反比例函数 的图象与一次函数 的图象的交点的横坐标为1和-3,则关于 的方程 的解是.13. 在 中, , , ,点 在 边上,点 为 边上的动点,点 、 分别为 , 的中点,则 的最小值是. 14. 如图, 、 是直线 上的两个定点,点 、 在直线 上运动(点 在点 的左侧), .已知 ,连接 、 、 ,把 沿 折叠得 .当 、 两点重合时, ;当 、 两点不重合时,若直线 与 距离为 .若以 、 、 、 为顶点的四边形是矩形, .
14. 如图, 、 是直线 上的两个定点,点 、 在直线 上运动(点 在点 的左侧), .已知 ,连接 、 、 ,把 沿 折叠得 .当 、 两点重合时, ;当 、 两点不重合时,若直线 与 距离为 .若以 、 、 、 为顶点的四边形是矩形, .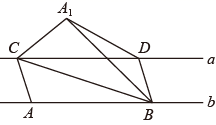
三、解答题
-
15. 计算:(1)、(2)、16. 化简代数式: ,直接写出 为何整数时,该代数式的值也为整数.17. 解下列方程(1)、(2)、18. 按下列要求画 ,使它的四个顶点以及对角线交点都在方格的顶点上,
 (1)、在图①中画 ,使它的周长是整数;(2)、在图②中画 ,使它的周长不是整数(请标出必要的字母与线段长度)19. 为了支持新冠肺炎疫情防控工作,某区积极响应党的号召,鼓励老师们踊跃捐款.为了了解该区老师们的捐款情况,抽取了部分老师的捐款金额进行统计,数据整理成如下尚不完整的统计表和统计图.
(1)、在图①中画 ,使它的周长是整数;(2)、在图②中画 ,使它的周长不是整数(请标出必要的字母与线段长度)19. 为了支持新冠肺炎疫情防控工作,某区积极响应党的号召,鼓励老师们踊跃捐款.为了了解该区老师们的捐款情况,抽取了部分老师的捐款金额进行统计,数据整理成如下尚不完整的统计表和统计图.某区教师捐款金额抽样统计表
组别
捐款金额(元)
人数
A
2
B
10
C
D
14
E
4
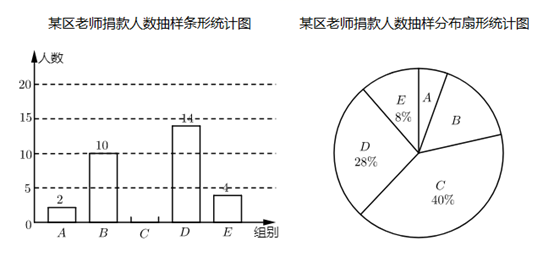 (1)、一共抽取了名老师;(2)、补全条形统计图,并算出扇形统计图中 组对应扇形的圆心角度数为 ▲ °;(3)、该社区共有1000名老师,请估计捐款金额超过300元的老师有多少名?20. 某中学八年级学生去距学校 的汤山园博园参观,一部分学生骑自行车先走,过了 后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.21. 如图,在四边形 中,对角线 与 相交于点 , , 平分 .
(1)、一共抽取了名老师;(2)、补全条形统计图,并算出扇形统计图中 组对应扇形的圆心角度数为 ▲ °;(3)、该社区共有1000名老师,请估计捐款金额超过300元的老师有多少名?20. 某中学八年级学生去距学校 的汤山园博园参观,一部分学生骑自行车先走,过了 后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.21. 如图,在四边形 中,对角线 与 相交于点 , , 平分 .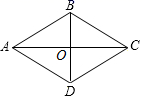 (1)、给出下列四个条件:① ;② ;③ ;④ ,上述四个条件中,选择一个合适的条件,使四边形 是菱形,这个条件可以是(填写一个序号即可);(2)、根据你所选择的条件,证明四边形 是菱形.22. 将 克糖放入水中,得到 克糖水,此时糖水的含糖量我们可以记为 .(1)、再往杯中加入 克糖,生活中的经验告诉我们糖水变甜了,用数学关系式可以表示为______;A、 B、 C、(2)、请证明你的选择.23.(1)、用配方法解一元二次方程除了课本的方法,也可以用下面的配方方式:
(1)、给出下列四个条件:① ;② ;③ ;④ ,上述四个条件中,选择一个合适的条件,使四边形 是菱形,这个条件可以是(填写一个序号即可);(2)、根据你所选择的条件,证明四边形 是菱形.22. 将 克糖放入水中,得到 克糖水,此时糖水的含糖量我们可以记为 .(1)、再往杯中加入 克糖,生活中的经验告诉我们糖水变甜了,用数学关系式可以表示为______;A、 B、 C、(2)、请证明你的选择.23.(1)、用配方法解一元二次方程除了课本的方法,也可以用下面的配方方式:将 两边同时乘以 并移项,得到 ,两边再同时加上 ,得( ▲ )2 .请用这样的方法解方程: ;
(2)、华裔数学家罗博深在2019年提出了一种全新的一元二次方程解法,对于 ,将等式左边进行因式分解,得到以下形式:(从这里可以看出方程的解为 , )
即
因为 ,所以 、 的平均数为 ,不妨设 , ,
利用 ,得 ,所以 ,即能求出 的值.
举例如下:解一元二次方程 ,由于 ,所以方程的两个根为 ,而 ,解得 ,所以方程的解为 , .
请运用以上方法解如下方程① ;②
24. (性质认识)如图,在函数 的图象上任取两点 、 向坐标轴作垂直,连接垂足 、 或 、 ,则一定有如下结论: , .
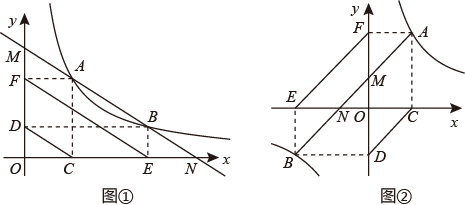 (1)、(数学理解)如图①,借助(性质认知)的结论,猜想 (填“>”、“=”或“<”);(2)、如图②,借助(性质认知)的结论,证明: ;(3)、(问题解决)如图③,函数 的图象与过原点的直线相交于 、 两点,点 是第一象限内图象上的动点(点 在点 的左侧),直线 分别交于 轴、 轴于点 、 ,连接 分别交 轴、 轴于点 、 .请证明: .
(1)、(数学理解)如图①,借助(性质认知)的结论,猜想 (填“>”、“=”或“<”);(2)、如图②,借助(性质认知)的结论,证明: ;(3)、(问题解决)如图③,函数 的图象与过原点的直线相交于 、 两点,点 是第一象限内图象上的动点(点 在点 的左侧),直线 分别交于 轴、 轴于点 、 ,连接 分别交 轴、 轴于点 、 .请证明: .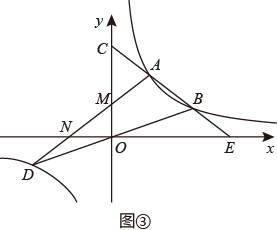 (4)、在第(3)问中,若 ,则 .
(4)、在第(3)问中,若 ,则 .