江苏省连云港市赣榆区、灌南县2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史． $2017$ 年 $5$ 月，世界围棋冠军柯洁与人工智能机器人 $AlphaGo$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
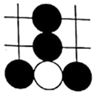2. 下列运算正确的是（）

A、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $3 + 2 \sqrt{2} = 5 \sqrt{2}$ D、 $4 \sqrt{3} - 3 \sqrt{3} = 1$

查看试题解析
3. 若 $\sqrt{3 - 2 x}$ 是二次根式，则 $x$ 的取值范围是（）

A、 $x < \frac{3}{2}$ B、 $x \leq \frac{3}{2}$ C、 $x > \frac{3}{2}$ D、 $x \geq \frac{3}{2}$

查看试题解析
4. 将分式 $\frac{x^{2}}{x + y}$ 中 $x ， y$ 的值都扩大到原来的3倍，则扩大后分式的值（）

A、扩大到原来的3倍 B、扩大到原来的9倍 C、不变 D、缩小到原来的 $\frac{1}{3}$

查看试题解析
5. 若关于x的方程 $\frac{x}{x - 1} - 2 = \frac{m}{x - 1}$ 有增根，则m的值为（）

A、2 B、1 C、0 D、-1

查看试题解析
6. 若反比例函数 $y = (2 m - 1) x^{m^{2} - 2}$ 的图象在第二、四象限，则 $m$ 的值是（）

A、-1或1 B、小于 $\frac{1}{2}$ 的任意实数 C、-1 D、不能确定

查看试题解析
7. 已知点 $P (x_{1} ， - 2)$ ， $Q (x_{2} ， 2)$ ， $R (x_{3} ， 3)$ 三点都在反比例函数 $y = \frac{a^{2} + 3}{x}$ 的图象上，则下列关系正确的是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{3} < x_{2} < x_{1}$ C、 $x_{1} < x_{3} < x_{2}$ D、 $x_{2} < x_{3} < x_{1}$

查看试题解析
8. 如图，线段 $A B$ 的长为 $8$ ，点 $D$ 在 $A B$ 上， $Δ A C D$ 是边长为 $3$ 的等边三角形，过点 $D$ 作与 $C D$ 垂直的射线 $D P$ ，过 $D P$ 上一动点 $G$ （不与 $D$ 重合）作矩形 $C D G H$ ，记矩形 $C D G H$ 的对角线交点为 $O$ ，连接 $O B$ ，则线段 $B O$ 的最小值为（）

A、5 B、4 C、 $4 \sqrt{3}$ D、 $5 \sqrt{3}$

查看试题解析

二、填空题

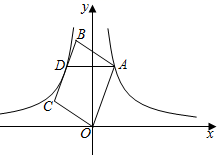
9. 已知一个样本中，样本容量为50，这50个数据分别落在5个小组内，第一、二、四、五小组的频数分别是2，10，10，20，则第三个小组的频率为.

查看试题解析
10. 已知 $\sqrt{12}$ 与最简二次根式 $\sqrt{2 a - 1}$ 是同类二次根式，则a的值是.

查看试题解析
11. 分式 $\frac{a}{3 b^{2}}$ 和 $\frac{5}{9 a^{2} b}$ 的最简公分母是．

查看试题解析
12. 计算：（ $\sqrt{5}$ ）²=

查看试题解析
13. 已知 $y = \frac{1}{x}$ 与y=x-3相交于点 $P (a ， b)$ ，则 $\frac{1}{a} - \frac{1}{b}$ 的值为.

查看试题解析
14. 已知关于 $x$ 的分式方程 $\frac{2}{x - 3} + \frac{x + a}{3 - x} = 2$ 的解为正数，则 $a$ 的取值范围是

查看试题解析
15. 如图，已知 $▱ A B C O$ 顶点 $A$ 在反比例函数 $y = \frac{2}{x} (x > 0)$ 的图象上，边 $B C$ 与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $D$ ，且 $A D / / x$ 轴，若 $S_{▱ A B C O} = 8$ ，则 $k =$

查看试题解析

三、解答题

16. 计算

(1)、 $2 \sqrt{18} - \sqrt{50} + \frac{1}{2} \sqrt{32}$

(2)、 $\frac{4}{\sqrt{2}} + {(\sqrt{2} - 1)}^{2}$

查看试题解析
17. 解方程

(1)、 $\frac{5}{x - 1} = \frac{1}{2 x + 1}$

(2)、 $\frac{1}{x - 2} + 2 = \frac{1 - x}{2 - x}$

查看试题解析
18. 先化简，再求值：( $1 - \frac{1}{a + 1}) \div \frac{a^{2} - a}{a + 1}$ ，其中 $a = 1 + \sqrt{3}$

查看试题解析
19. 为了预防流感，某校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（mg0与时间x（min）成正比例，药物燃烧完后，y与x成反比例，现测得药物10（min）燃毕，此时室内空气每立方米的含药量为8mg请根据题中所提供的信息，解答下列问题

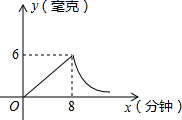(1)、药物燃烧时，y关于x的函数关系式为，自变量x的取值范围是

(2)、药物燃烧后，y关于x的函数关系式为

(3)、研究表明，当空气中，每立方米的含药量低于1.6mg时，学生方可进教室，那么从消毒开始时，至少需要多少分钟后，学生才能回到教室？

查看试题解析
20. 在矩形ABCD中，连接AC，AC的垂直平分线交AC于点O，分别交AD、BC于点E、F，连接CE和AF．

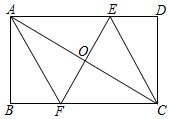(1)、求证：四边形AECF为菱形；

(2)、若AB＝4，BC＝8，求菱形AECF的面积．

查看试题解析
21. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象相交于A、B两点，且与x轴交于点 C，点A的坐标为（2，3），点B的坐标为（-6，n）.

(1)、求一次函数与反比例函数的解析式；

(2)、连接AO、OB，求△AOB的面积；

(3)、结合图象直接写出不等式组 $\frac{m}{x} \leq k x + b < 0$ 的解集.

查看试题解析
22. 以诗育德，以诗启智，以诗怡情，以诗塑美，万州区某中学开展诗歌创作比赛，积极营造诗韵书香学生生活.年级决定购买 $A, B$ 两种笔记本奖励在此次创作比赛中的优秀学生，已知 $A$ 种笔记本的单价比 $B$ 种笔记本的单价便宜 $3$ 元，已知用1800元购买 $A$ 种笔记本的数量是用1350元购买 $B$ 种笔记本的数量的2倍.

(1)、求 $A$ 种笔记本的单价；

(2)、根据需要，年级组准备购买 $A, B$ 两种笔记本共100本，其中购买 $A$ 种笔记本的数量不超过 $B$ 种笔记本的二倍.设购买 $A$ 种笔记本 $m$ 本，所需经费为 $W$ 元，试写出 $W$ 与 $m$ 的函数关系式，并请你根据函数关系式求所需的最少经费.

查看试题解析
23. 如图，在平面直角坐标系中，A （6，0）、B（0， 4）是矩形OACB的两个顶点，双曲线 $y = \frac{k}{x}$ （k≠0，x>0）经过AC的中点D，点E是矩形OACB与双曲线 $y = \frac{k}{x}$ 的另一个交点，

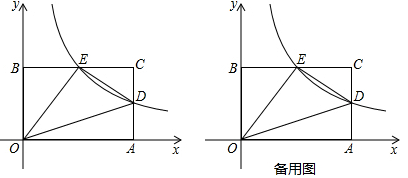(1)、点D的坐标为，点E的坐标为.

(2)、动点P在第一象限内，且满足 $S_{△ P B O} = \frac{8}{9} S_{△ O D E}$ .
①若点P在这个反比例函数的图象上，求点P的坐标；

②连接PO、PE，当PO-PE的值最大时，求点P的坐标；

③若点Q是平面内一点，使得以A、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标.

查看试题解析
24. 在 $Δ A B C$ 中， $∠ B A C = 90^{°} ， A B = A C$ ，点 $D$ 为直线 $B C$ 上一动点（点 $D$ 不与 $B ， C$ 重合），以 $A D$ 为边在 $A D$ 右侧作正方形 $A D E F$ ，连接 $C F$

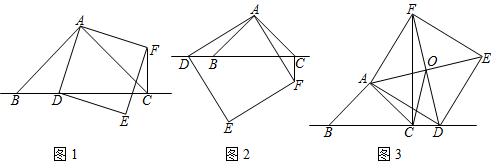(1)、探究猜想如图1，当点 $D$ 在线段 $B C$ 上时，
① $B C$ 与 $C F$ 的位置关系为；

② $B C ， C D ， C F$ 之间的数量关系为；

(2)、深入思考：如图2，当点 $D$ 在线段 $C B$ 的延长线上时，结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.

(3)、拓展延伸如图3，当点 $D$ 在线段 $B C$ 的延长线上时，正方形 $A D E F$ 对角线交于点 $O$ .若已知 $A B = 2 \sqrt{2} ， C D = \frac{1}{4} B C$ ，请求出 $O C$ 的长.

查看试题解析