福建省南平市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-27 类型:期末考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列式子与 可以进行合并的是( )A、 B、 C、 D、3. 在平行四边形ABCD中,∠A+∠C=120°,则∠D等于( )A、30° B、60° C、120° D、150°4. 下列不能判断是正方形的有( )A、对角线互相垂直的矩形 B、对角线相等的矩形 C、对角线互相垂直且相等的平行四边形 D、对角线相等的菱形5. 在平面直角坐标系中,已知 , 是一次函数 图象上的两个点,则 与 的大小关系为( )A、 B、 C、 D、不能确定6. 在△ABC中,若∠B+∠C=90°,则( )A、BC=AB+AC B、AC2=AB2+BC2 C、AB2=AC2+BC2 D、BC2=AB2+AC27. 在下列四个选项中,不符合直线 的性质的是( )A、经过第一、二、三象限 B、 随 的增大而增大 C、与 轴相交于点(2,0) D、与 轴相交于点(0,2)8. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,在相同条件下各小组的成绩如下表所示,若要从中选择一个小组参加年级的比赛,那么应选( )
甲组
乙组
丙组
丁组
平均分
85
90
88
90
方差
3.5
3.5
4
4.2
A、甲组 B、乙组 C、丙组 D、丁组9. 已知四个三角形分别满足下列条件:①一个内角等于另两个内角之和;②三个内角度数之比为3∶4∶5;③三边长分别为7,24,25;④三边长之比为5∶12∶13.其中直角三角形有( )A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系中,点 在第一象限,且 ,点 的坐标为(4,0),设 的面积为 ,则下列图象中,能正确反映 与 之间的函数关系式的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 化简: .12. 一组数据是4,x,5,10,11共五个数,其平均数为8,则这组数据的众数是.13. 矩形的两条对角线的夹角为 ,对角线长为12,则较短的边长为.14. 我国古代数学著作《九章算术》有一个问题:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处,1丈=10尺,那么折断处离地面的高度是尺.
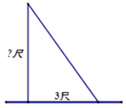 15. 如图,已知直线 与直线 相交于点 ,则关于 的不等式 的解集为.
15. 如图,已知直线 与直线 相交于点 ,则关于 的不等式 的解集为. 16. 如图,在边长为6的菱形 中, , 为 上方一点,且 ,则 的最小值为.
16. 如图,在边长为6的菱形 中, , 为 上方一点,且 ,则 的最小值为.
三、解答题
-
17. 计算: .18. 如图,在▱ABCD中,DE⊥AB , BF⊥CD , 垂足分别为E , F . 求证:BE=DF .
 19. 如图是一个 的正方形网格,已知每个小正方形的边长均为1,每个小正方形的顶点称为格点,请按要求解答下列问题:
19. 如图是一个 的正方形网格,已知每个小正方形的边长均为1,每个小正方形的顶点称为格点,请按要求解答下列问题: (1)、如图,满足线段 的格点 共有个;(2)、试在图中画出一个格点 ,使其为等腰三角形, ,且 的内部只包含4个格点(不包含在 边上的格点).20. “新型冠状病毒肺炎”疫情牵动着亿万国人的心,为进一步加强疫情防控工作,某校利用网络平台进行疫情防控知识测试,测试题共10小题,每小题10分.小明同学对八(1)班和八(2)班两个班各40名同学的测试成绩(单位:分)进行了整理和分析,统计数据如下:
(1)、如图,满足线段 的格点 共有个;(2)、试在图中画出一个格点 ,使其为等腰三角形, ,且 的内部只包含4个格点(不包含在 边上的格点).20. “新型冠状病毒肺炎”疫情牵动着亿万国人的心,为进一步加强疫情防控工作,某校利用网络平台进行疫情防控知识测试,测试题共10小题,每小题10分.小明同学对八(1)班和八(2)班两个班各40名同学的测试成绩(单位:分)进行了整理和分析,统计数据如下:①八(1)班成绩频数分布直方图如图:

②八(2)班成绩平均分的计算过程如下:
(分);
③数据分析如下:
班级
平均数
中位数
众数
方差
八(1)班
82.5
90
158.75
八(2)班
80.5
75
174.75
根据以上信息,解答下列问题:
(1)、 , ;(2)、你认为班的成绩更加稳定,理由是;(3)、在本次测试中,八(1)班甲同学和八(2)班乙同学的成绩均为80分,你认为两人在各自班级中谁的成绩排名更靠前?请说明理由.21. 如图,在平面直角坐标系中,直线 经过点 和点 ,与 轴交于点 ,直线 经过点 ,且与 轴的负半轴交于点 ,若 的面积为3. (1)、求点 , 的坐标;(2)、求直线 的解析式.22. 如图,在四边形 中, , ,对角线 , 相交于点 ,AC平分 ,过点 作 交 的延长线于点 ,连接 .
(1)、求点 , 的坐标;(2)、求直线 的解析式.22. 如图,在四边形 中, , ,对角线 , 相交于点 ,AC平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形:(2)、若 ,且 ,求 的长.23. 如图,在平面直角坐标系中,直线 与 轴、 轴分别相交于 , 两点,过原点的直线 与直线 相交于点 ,且 .
(1)、求证:四边形 是菱形:(2)、若 ,且 ,求 的长.23. 如图,在平面直角坐标系中,直线 与 轴、 轴分别相交于 , 两点,过原点的直线 与直线 相交于点 ,且 .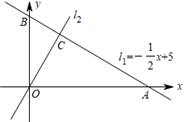 (1)、求点 的坐标及直线 的解析式;(2)、若直线 ,且直线 , , 不能围成三角形,直接写出 的值.24. 如图,在平行四边形 中, 为 边上一点,且 .
(1)、求点 的坐标及直线 的解析式;(2)、若直线 ,且直线 , , 不能围成三角形,直接写出 的值.24. 如图,在平行四边形 中, 为 边上一点,且 . (1)、求证: ;(2)、若 ,求 的度数;(3)、若 , , ,求 的长.25. 探究活动一:
(1)、求证: ;(2)、若 ,求 的度数;(3)、若 , , ,求 的长.25. 探究活动一: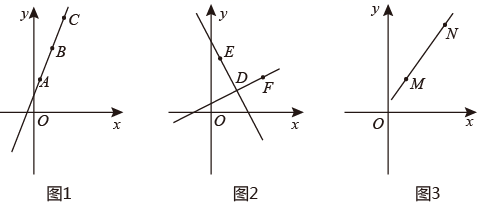
如图1,某数学兴趣小组在研究直线上点的坐标规律时,发现在直线 上的三点 , , ,有 , , ,兴趣小组提出猜想:若直线 上任意两点 , ,则 是定值.通过多次验证和查阅资料得知,猜想成立, 是定值,并且是直线 中的 ,叫做这条直线的斜率.
(1)、请你应用以上规律直接写出过 , 两点的直线 的斜率 .(2)、探究活动二: 数学兴趣小组继续深入研究直线的“斜率”问题,得到正确结论:当任意两条不和坐标轴平行的直线互相垂直时,这两条直线的斜率之积是定值.
如图2,直线 与直线 垂直于点 ,且 , , .请求出直线 与直线 的斜率之积.并写出你发现的结论.(3)、综合应用:
如图3, , ,请结合探究活动二的结论,求出过点 且与直线 垂直的直线的解析式.