福建省龙岩市五县市区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{2 x - 6}$ 在实数范围内是二次根式，则 $x$ 的取值范围是（）

A、 $x$ ≥3 B、 $x$ ≤3 C、 $x$ ＞3 D、 $x \neq 3$

查看试题解析
2. 下列计算结果正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $2 \sqrt{2} \times 2 \sqrt{3} = 2 \sqrt{6}$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{27} \div \sqrt{3} = 3$

查看试题解析
3. 在平行四边形ABCD中，∠A=2∠B ，则∠C的度数是（）

A、60° B、90° C、120° D、135°

查看试题解析
4. 某女子羽毛球球队 $6$ 名队员身高（单位 $cm$ ）是170，174，178，180， 180，
184，因某种原因身高为 $174 cm$ 的队员退役，补上一位身高为 $178 cm$ 的队员后，该女子羽毛球队有关队员身高的数据正确的是（）

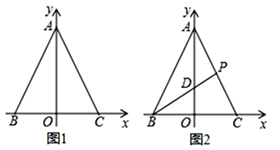
A、平均数变大，中位数不变 B、平均数变大，中位数变大 C、平均数变小，中位数不变 D、平均数变小，中位数变大

查看试题解析
5. 如图， $R t △ A B C$ 中， $∠ A C B = 90 ° ， C D ⊥ A B$ 于点D ，若 $∠ A = 60 ° ， A D = 1$ ，则 $B C$ 的长为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $\sqrt{6}$

查看试题解析
6. 如图，四边形ABCD的对角线交于点O ，下列不能判定四边形ABCD为平行四边形的是（）

A、AB＝CD ， AD＝BC B、∠ABC＝∠ADC ， AB∥CD C、OA＝OC ， OB＝OD D、AB∥CD ， AD＝BC

查看试题解析
7. 如图是由边长为1的小正方形组成的网格，△ABC的顶点A，B，C均在格点上，BD⊥AC于点D，则BD的长为（）

A、 $\frac{12}{5}$ B、 $\frac{24}{5}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
8. 如图，在 $Rt Δ A B C$ 中， $∠ A C B = 90 °$ ，点 $D ， E$ 分别是边 $A B ， A C$ 的中点，延长 $B C$ 至 $F$ ，使 $C F = \frac{1}{2} B C$ ，若 $A B = 12$ ，则EF的长是（）

A、7 B、6 C、5 D、4

查看试题解析
9. 如图是甲、乙两家商店销售同一种产品的销售价 $y$ （元）关于销售量 $x$ （件）的函数图象.给出下列说法，其中说法不正确的是（）

A、售2件时，甲、乙两家的售价相同 B、买1件时，买乙家的合算 C、买3件时，买甲家的合算 D、乙家的1件售价约为3元

查看试题解析
10. 如图1，在菱形 $A B C D$ 中，动点P从点B出发，沿折线B→C→D→B运动，设点P经过的路程为x， $△ A B P$ 的面积为y.把y看作x的函数，函数的图象如图2所示，则图2中的a等于（）

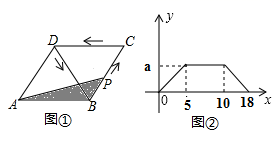A、25 B、20 C、12 D、 $8 \sqrt{3}$

查看试题解析

二、填空题

11. 计算： $\sqrt{2} + \sqrt{18}$ = ．

查看试题解析
12. 已知点P（3，5）在一次函数y＝x+b的图象上，则b＝.

查看试题解析
13. 若一组数据4，9，5，m ， 3的平均数是5，则这组数据的众数是．

查看试题解析
14. 如图，平行四边形 $A B C D$ 中， $D E$ 平分 $∠ A D C$ 交边 $B C$ 于点 $E$ ， $A D = 8$ ， $A B = 5$ ，则 $B E =$ ．

查看试题解析
15. 如图正三角形 $A B C$ 与正方形 $C D E F$ 的顶点 $B ， C ， D$ 三点共线，动点 $P$ 沿着 $C A$ 由 $C$ 向 $A$ 运动．连接 $E P$ ，若 $A C = 10$ ， $C F = 8$ ．则 $E P$ 的最小值是．

查看试题解析

三、解答题

16. 将一副三角板按如图拼接，使两斜边重合，取 $B D$ 的中点 $E$ ，连接 $A E ， C E ， A C$ ，则 $∠ E A C =$ ．

查看试题解析
17. 计算： $\sqrt{6} + {(- 2 \sqrt{3})}^{2} - \sqrt{\frac{1}{3}} \div \frac{1}{\sqrt{18}}$ ．

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $A D = B C$ ，连接 $B D$ ， $E$ 是 $B C$ 延长线上一点，连接 $D E$ ，若 $B D = D E ， ∠ E = ∠ A D B$ ，求证 $∠ A = ∠ B C D$ ．

查看试题解析
19. 如图，连接四边形 $A B C D$ 的对角线 $A C$ ，已知 $∠ B = 90 ° ， B C = 1 ， ∠ B A C = 30 ° ， C D = 2 ， A D = 2 \sqrt{2}$ ．

(1)、求证： $Δ A C D$ 是直角三角形；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
20. 在平面直角坐标系中，一次函数 $y = k x + b$ （k ， b都是常数，且 $k \neq 0$ ）的图象经过点 $(1 ， 0)$ 和 $(0 ， - 1)$

(1)、当 $- 1 < x \leq 2$ 时，求y的取值范围．

(2)、已知点 $P (m ， n)$ 在该函数的图象上，且 $m + n = 5$ ，求点P的坐标．

查看试题解析
21. 如图，有一块三边长分别为 $3cm，4cm，5cm$ 的三角形硬纸板，现要从中剪下一块底边长为 $5cm$ 的等腰三角形．

(1)、在图中用没有刻度的直尺和圆规作出一个符合要求的等腰三角形（不写作法，保留作图痕迹）．

(2)、在（1）的条件下，求剪下等腰三角形的最大面积．

查看试题解析

22. 已知小明与小华在学校的五次数学竞赛培训时测试总成绩相同，下表是两人各次成绩的统计表，现要从这两名学生中选择一名学生去参加全国数学竞赛，需要对他们的培训成绩进行统计分析，请完成下列问题：

	第1次	第2次	第3次	第4次	第5次
小明的成绩	90	70	80	100	60
小华的成绩	70	90	90	$a$	70

(1)、

a

＝，

\bar{x_{小 华}}

＝；

(2)、请在图中完成表示小华成绩变化情况的折线：

(3)、

S^{2}_{小 明} = 200

，请你计算小华的方差；

(4)、根据以上数据说明选择小明或小华参加全国数学竞赛的理由．

查看试题解析

23. 某服装公司在新春到来之际，新上市A型和B型两款童装，准备将80件A型童装和120件B型童装分配给甲乙两个电商平台专实店销售．A型童装成本价90元，B型童装成本价80元，其中140件给甲电商平台专卖店，60件给乙电商平台专卖店，且都能卖完．两电商平台专卖店销售这两种童装每件的价格（元）如表：

A型（元）

B型（元）

甲店

190

170

乙店

170

180

(1)、设分配给甲电商专卖店A型产品x件 $(20 ⩽ x ⩽ 80)$ ，如果记这家服装公司卖出这200件童装的总利润为y（元），求y关于x的函数关系式．

(2)、如果要使得总利润最大，服装应当如何分配？最大利润是多少？

查看试题解析
24. 如图，在边长为 $1$ 的正方形 $A B C D$ 中， $E$ 是边 $C D$ 的中点，点 $P$ 是边 $A D$ 上一点(与点 $A ， D$ 不重合)，射线 $P E$ 与 $B C$ 的延长线交于点 $Q$ ．

(1)、求证： $Δ P D E$ ≌ $Δ Q C E$ ；

(2)、若点 $F$ 是 $P B$ 的中点，连接 $A F$ ，当 $P B = P Q$ 时．
①求证：四边形 $A F E P$ 是平行四边形；

②已知四边形 $A F E P$ 是菱形，求 $\frac{A P}{A B}$ 的值．

查看试题解析
25. 如图1，在平面直角坐标系中，点 $O$ 是坐标原点，直线 $y = 2 x + 6$ 交 $x$ 轴于点 $B$ ，交 $y$ 轴于点 $A$ ，且 $A O = B C$ ．

(1)、求直线 $A C$ 的解析式；

(2)、如图2，点 $P$ 在线段 $A C$ 上（不与 $A ， C$ 重合），连接 $P B$ 交 $O A$ 于点 $D$ ，设点 $P$ 的横坐标为 $t$ ， $Δ A B P$ 的面积为 $S$ ，求 $S$ 与 $t$ 之间的函数解析式；

(3)、在图2中， $∠ P B C = 30 °$ 时，求 $Δ A B P$ 的面积．

查看试题解析

	A型（元）	B型（元）
甲店	190	170
乙店	170	180